Tutorial about the spin¶
Properties related to spin (spin polarized calculations, ferro- ferri- magnetic materials, and spin-orbit coupling).¶
This tutorial aims at showing how to get the following physical properties:
- the total magnetization of a ferromagnetic (or ferrimagnetic) material
- the estimation of the atom magnetic moment
- analyse the total density of states per spin direction
- analyse the density of states per atom and per spin direction
- effect of spin-orbit coupling for a non magnetic system
- non-collinear magnetism (not yet)
- spin-orbit coupling and magnetocristalline anisotropy (not yet)
You will learn to use features of ABINIT which deal with spin.
This tutorial should take about 1.5 hour.
Note
Supposing you made your own installation of ABINIT, the input files to run the examples are in the ~abinit/tests/ directory where ~abinit is the absolute path of the abinit top-level directory. If you have NOT made your own install, ask your system administrator where to find the package, especially the executable and test files.
In case you work on your own PC or workstation, to make things easier, we suggest you define some handy environment variables by executing the following lines in the terminal:
export ABI_HOME=Replace_with_absolute_path_to_abinit_top_level_dir # Change this line
export PATH=$ABI_HOME/src/98_main/:$PATH # Do not change this line: path to executable
export ABI_TESTS=$ABI_HOME/tests/ # Do not change this line: path to tests dir
export ABI_PSPDIR=$ABI_TESTS/Psps_for_tests/ # Do not change this line: path to pseudos dir
Examples in this tutorial use these shell variables: copy and paste
the code snippets into the terminal (remember to set ABI_HOME first!) or, alternatively,
source the set_abienv.sh script located in the ~abinit directory:
source ~abinit/set_abienv.sh
The ‘export PATH’ line adds the directory containing the executables to your PATH so that you can invoke the code by simply typing abinit in the terminal instead of providing the absolute path.
To execute the tutorials, create a working directory (Work*) and
copy there the input files of the lesson.
Most of the tutorials do not rely on parallelism (except specific tutorials on parallelism). However you can run most of the tutorial examples in parallel with MPI, see the topic on parallelism.
1 A ferromagnetic material: bcc Fe¶
Before beginning, you might consider to work in a different subdirectory, as for the other tutorials. Why not Work_spin?
The file tspin_x.abi in $ABI_TESTS/tutorial/Input lists the input files for the spin tutorials. You can copy the first one in the Work_spin directory with:
cd $ABI_TESTS/tutorial/Input
mkdir Work_spin
cd Work_spin
cp ../tspin_1.abi .
# In this input file, the location of the information on this or that line # is not important : a keyword is located by the parser, and the related # information should follow. # The "#" symbol indicate the beginning of a comment : the remaining # of the line will be skipped. # Fe normal bcc structure for test of a ferromagnetic calculation # The first dataset is without magnetization for comparison ndtset 2 # Magnetism: spin related quantities (only second dataset) spinat2 0.0 0.0 4.0 nsppol2 2 # cutoff, k-points: ecut 18.0 ngkpt 4 4 4 nshiftk 1 shiftk 0.5 0.5 0.5 # SCF: nstep 50 tolvrs 1.0d-10 # Crystal cell definition: natom 1 ntypat 1 znucl 26 typat 1 xred 0.0 0.0 0.0 acell 3*5.42 rprim -0.5 0.5 0.5 0.5 -0.5 0.5 0.5 0.5 -0.5 # Electron occupation: occopt 3 nband 10 tsmear 0.01 # printing: prtdos 1 prtden 1 # Pseudo: pp_dirpath "$ABI_PSPDIR" pseudos "Pseudodojo_nc_sr_04_pw_standard_psp8/Fe.psp8" ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tspin_1.abo, tolnlines= 1, tolabs= 1.010e-09, tolrel= 2.000e-06 #%% [paral_info] #%% max_nprocs = 2 #%% [extra_info] #%% authors = Unknown #%% keywords = NC #%% description = #%% Fe normal bcc structure for test of a ferromagnetic calculation #%% The first dataset is without magnetization for comparison #%%<END TEST_INFO>
You can now run the calculation with:
abinit tspin_1.abi > log > err &
In the mean time the calculation is done, have a look at the input file, and read it carefully. Because we are going to perform magnetic calculations, there are two new types of variables related to magnetism:
You will work with a low ecut (=18Ha) and a small k-point grid (defined by ngkpt) of 4x4x4 Monkhorst-Pack grid. It is implicit that in real life, you should do a convergence test with respect to both ecut and ngkpt parameters and this is even more important with magnetism that involves low energy differences and small magnetization density values.
This basic first example will compare two cases, one that do not take into account magnetism and one that take into account it (done through two datasets in the input, the dataset 1 does not include magnetism and dataset 2 includes it). We now look at the output file. In the magnetic case (dataset 2), the electronic density is split into two parts, the “Spin-up” and the “Spin-down” parts to which correspond different Kohn-Sham potentials and different sets of eigenvalues whose occupations are given by the Fermi-Dirac function (without the ubiquitous factor 2).
For the first k-point, for instance, we get:
(no magnetism)
2.00000 2.00000 2.00000 2.00000 2.00000 1.99999 1.99999 1.28101 1.28101 0.35284
(magnetic case)
(SPIN UP)
1.00000 1.00000 1.00000 1.00000 1.00000 1.00000 1.00000 0.97826 0.97826 0.68642
(SPIN DOWN)
1.00000 1.00000 1.00000 1.00000 1.00000 0.99995 0.99995 0.05851 0.05851 0.01699
We note that the occupations of the magnetic case are different for up and down spin channels, which means that the eigenvalues are shifted (which is in turn due to a shift of the exchange-correlation potential and therefore of the effective potential). You can have a look at the output file to compare spin-up and down eigenvalues:
(up channel:)
-3.09143 -1.74675 -1.74675 -1.74418 0.25777 0.36032 0.36032 0.46350 0.46350 0.49374
(dn channel:)
-3.04218 -1.69171 -1.69171 -1.68906 0.27331 0.40348 0.40348 0.52935 0.52935 0.54215
Now you can move down in the output file and look at the following section:
Integrated electronic and magnetization densities in atomic spheres:
---------------------------------------------------------------------
Radius=ratsph(iatom), smearing ratsm= 0.0000. Diff(up-dn)=approximate z local magnetic moment.
Atom Radius up_density dn_density Total(up+dn) Diff(up-dn)
1 2.00000 7.658786 6.158329 13.817115 1.500458
---------------------------------------------------------------------
Sum: 7.658786 6.158329 13.817115 1.500458
Total magnetization (from the atomic spheres): 1.500458
Total magnetization (exact up - dn): 1.571040
======================================================================
In the last line, it is reported the total magnetization of the whole unit cell (in unit of \mu_B - Bohr’s magneton), which correponds to the difference between the integrated up and down densities, here we have 1.571040 \mu_B. It is also reported the same difference but as integrated into spheres around each atom (here we have only one atom), which gives here 1.500458 \mu_B on iron atom. The integrated magnetization in atomic spheres is an approximation, one should always check that the sum of the integrated atomic magnetization “from the atomic sphere” is very close to the exact up-dn unit cell magnetization. In the case of dataset 1 without magnetism, only the integrated electronic density is reported since there is no distinction between up and down spin channels.
You can look at the total energy of dataset 1 and 2:
etotal1 -1.2342819713E+02
etotal2 -1.2343141307E+02
The energy of the magnetic calculation is lower than the non-magnetic one, which is expected for a magnetic crystal (the system gains energy through the extra degrees of freedom given by the spins). Finally, you can also remark that the stress tensor is affected by the presence of magnetism. This would also be true for the forces, but we don’t remark it here because we are in high symmetry symmetry structure (all the forces are zeroed by symmetry), however this would be apparent for a less symmetric material.
It is interesting to consider in more detail the distribution of eigenvalues for each spin channel, which is best done by looking at the respective densities of state (DOS). To this end we have set prtdos = 1 in the input file that will print the up and down DOS (as soon as nsppol = 2). The DOS data can be found in the files tspin_1o_DS1_DOS and tspin_1o_DS2_DOS for the non-magnetic and the magnetic cases respectively, which can be used with a plotting software. Traditionally, in order to enhance visibility, the DOS of minority spin electrons is done using negative values. If we compare the DOS of the magnetized system (the Fermi energy is highlighted by a vertical dashed line):

and the non-magnetized system:
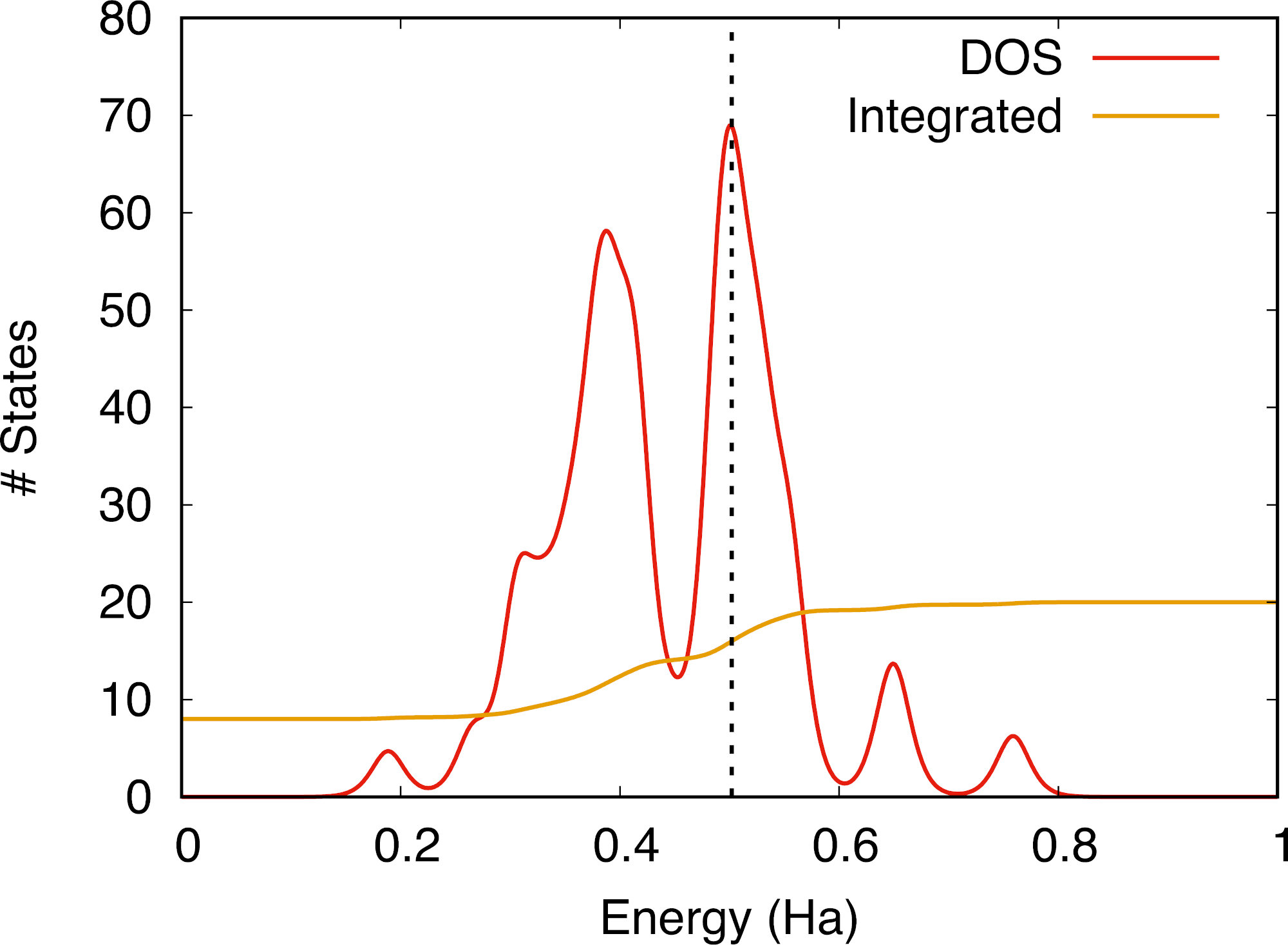
We observe that the up and down DOS channels have been “shifted” with respect to each other, which is a footprint of the presence of non-zero total magnetization in the crystal (either ferro- or ferri-magnetic). The integrated DOS yields the number of electrons for each spin direction, and we see that the magnetization arises from the fact that there are more up than down electrons at the Fermi level.
The magnetization is from the up channels because we initialized spinat with positive values. We could initialize it to a negative value to have negative magnetization. spinat serves two purposes: it is a way to initially break the spin symmetry (up/down), and also to start with an initial magnetic moment, ideally close enough to the final DFT one but sometimes a final non-zero magnetic moment on the atoms is obtained by initializing spinat to larger values than the formal one (in spin DFT there can be several local minima for the total energy and depending on your starting point you can end up in different local minima).
Note that spinat has three components (i.e. for x, y and z directions) for each atom but in the absence of spin-orbit coupling (collinear calculation) there is no relation between the direction of magnetization and the crystal axes. In these collinear magnetism calculations, only the z component of the spins is read to define the amplitude of the atomic magnetic moment (treated as a scalar value, i.e. only sign and amplitude matter).
The self-consistent loop is affecting both the density (like in the non-magnetic case) as well as the spin-magnetization. For this reason, it might be more difficult to reach convergence in the magnetic cases than in the non-magnetic cases. Not only starting with a large enough magnetic moment might help to converge toward the correct magnetic ground sate, but also modified (tighter) convergence parameters might be needed. For example, in the case of Cobalt, in order to obtain the correct (non-zero) magnetic moment, a rather dense k-point sampling in the Brillouin zone must be used (e.g. 16x16x16), with a rather small value of tsmear. The convergence of a magnetic calculation a smaller value of tolrde (e.g. 0.001 instead of the default 0.005), a larger value of nline (e.g. 6 to 12 instead of the default 4) and/or reducing the mixing parameters diemix and mostly diemixmag.
2 An antiferromagnetic example: fcc Fe¶
Well sort of....
Actually, fcc Fe, displays many complicated structures, in particular spin spirals. A spiral is characterized by a direction along an axis, an angle of the magnetization with respect to this axis and a step after which the magnetization comes full circled. A very simple particular case is when the angle is 90°, the axis is <100> and the step is the unit cell side: spin directions alternate between planes perpendicular to the <100> axis yielding a “spiral stairway”:
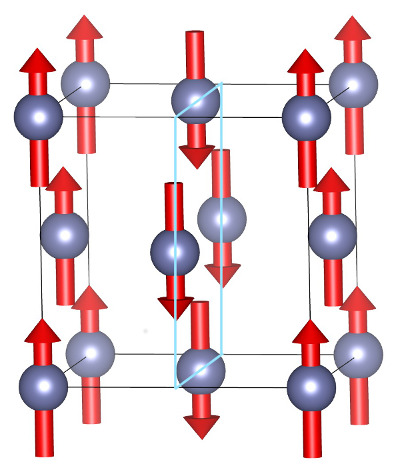
For instance, if the atom at [x,y,0] possesses an “up” magnetization, the atom at [x+½,y,½] would possess a down magnetization etc… To describe such a structure, a unit cell with two atoms is sufficient, [0,0,0] and [½,0,½]. The two atoms will be given opposite magnetization with the help of the variable spinat.
Copy the file $ABI_TESTS/tutorial/Input/tspin_2.abi in Work_spin.
# Added by runtests.py output_file = "tspin_2.abo" indata_prefix = "tspin_2i" outdata_prefix = "tspin_2o" tmpdata_prefix = "tspin_2t" # end runtests.py section # Fe fcc structure with two atoms per unit cell for test of antiferromagnetic order # This is the simplest fcc structure compatible with a X point spiral # cutoff, k-points: ecut 25.0 ngkpt 4 4 2 nshiftk 1 shiftk 0.5 0.5 0.5 # SCF: tolwfr 1.0d-7 nstep 70 # Magnetism: Antiferromagnic order nsppol 1 nspden 2 spinat 0.0 0.0 4.0 0.0 0.0 -4.0 # Crystal cell definition: natom 2 ntypat 1 znucl 26 typat 1 1 xred 0.0 0.0 0.0 0.5 0.0 0.5 acell 3*6.60 rprim 0.5 -0.5 0.0 0.5 0.5 0.0 0.0 0.0 1.0 # Treating electron occupation: nband 20 occopt 3 tsmear 0.001 # Printing: prtdos 1 prtden 1 # Pseudo: pp_dirpath "$ABI_PSPDIR" pseudos "Pseudodojo_nc_sr_04_pw_standard_psp8/Fe.psp8" ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tspin_2.abo, tolnlines = 60, tolabs = 0.000e+00, tolrel = 0.000e+00, fld_options=-medium #%% [paral_info] #%% max_nprocs = 4 #%% [extra_info] #%% authors = Unknown #%% keywords = NC #%% description = #%% Fe fcc structure with two atoms per unit cell for test of antiferromagnetic #%% This is the simplest fcc structure compatible with a X point spiral #%%<END TEST_INFO>
This is your input file.
You can run the calculation, then you should edit the tspin_2.in file, and briefly look at the two changes with respect to the file tspin_1.abi: the unit cell basis vectors rprim, and the new spinat.
Note also that we use now nsppol = 1 and nspden = 2: this combination of values
is only valid when performing a strictly antiferromagnetic (AFM) calculation:
nspden = 2 means that we have 2 independent components for the charge density
while nsppol = 1 means that we have 1 independent component for the wave-functions.
In that case, ABINIT uses the so-called Shubnikov symmetries, to perform
calculations twice faster than with nsppol = 2 and nspden = 2
(spin up and down channels are equivalent by symmetry in the case of perfect AFM cases).
The symmetry of the crystal is not the full fcc symmetry anymore, since the
symmetry must now preserve the magnetization of each atom.
ABINIT is nevertheless able to detect such symmetry belonging to the Shubnikov groups
and correctly finds that the cell is primitive, which would not be the case
if we had the same vector spinat on each atom (FM case).
If we now run this AFM calculation, its computation time is approximately 10-20 seconds on a recent CPU. If we look at the eigenvalues and occupations, they are again filled with a factor 2, which comes from the symmetry considerations aforementioned, and not from the “usual” spin degeneracy: the potential for spin-up is equal to the potential for spin-down, shifted by the antiferromagnetic translation vector. Eigenenergies are identical for spin-up and spin-down, but wavefunctions are shifted one with respect to the other.
kpt# 1, nband= 20, wtk= 0.25000, kpt= 0.1250 0.1250 0.2500 (reduced coord)
-2.75606 -2.71227 -1.51270 -1.50656 -1.50211 -1.46164 -1.45614 -1.45485
0.25613 0.34136 0.38202 0.41368 0.41915 0.46180 0.48400 0.50628
0.52100 0.54004 0.56337 0.64500
occupation numbers for kpt# 1
2.00000 2.00000 2.00000 2.00000 2.00000 2.00000 2.00000 2.00000
2.00000 2.00000 2.00000 2.00000 2.00000 2.00000 2.00000 2.00000
1.95186 0.00000 0.00000 0.00000
The total magnetization being zero we can question how do we know we have magnetic order? Indeed, the DOS will not be useful since we have as many up and down electrons.
We can however look at the integrated magnetization around each atom to have an indication of the magnetic moment carried by each atom:
Integrated electronic and magnetization densities in atomic spheres:
---------------------------------------------------------------------
Radius=ratsph(iatom), smearing ratsm= 0.0000. Diff(up-dn)=approximate z local magnetic moment.
Atom Radius up_density dn_density Total(up+dn) Diff(up-dn)
1 2.00000 7.748236 6.575029 14.323265 1.173206
2 2.00000 6.575029 7.748236 14.323265 -1.173206
---------------------------------------------------------------------
Sum: 14.323265 14.323265 28.646531 -0.000000
Total magnetization (from the atomic spheres): -0.000000
Total magnetization (exact up - dn): -0.000000
================================================================================
which gives (dependent on the radius used to project the charge density):
magnetization of atom 1= 1.173206
magnetization of atom 2=-1.173206
Another way to get integrated atom magnetization can be done by using the utility cut3d which yields an interpolation of the magnetization at any point in space. cut3d is one of the executables of the ABINIT package and is installed together with abinit. For the moment cut3d is interactive, and we will use it through a very primitive script (written in Python) to perform a rough estimate of the magnetization on each atom. You can have a look at the magnetization.py program, and note (or believe) that it does perform an integration of the magnetization in a cube of side acell/2 around each atom; if applicable, you might consider adjusting the value of the “CUT3D” string in the Python script.
Copy it in your Work_spin directory. If you run the program, by typing
python magnetization.py
you will see the result:
For atom 0 magnetic moment 1.2336144871839712
For atom 1 magnetic moment -1.2336216848949257
which also show that the magnetizations of the two atoms are opposite. The values of the atom magnetization is a bit different than the ones from the ABINIT output because it uses a slightly different integration paramters.
3 Another look at fcc Fe¶
Instead of treating fcc Fe directly as an AFM material, we will not make any hypotheses on its magnetic structure, and run the calculation like the one for bcc Fe, anticipating only that the two spin directions are going to be different. We will not even assume that the initial spins are of the same magnitude.
You can copy the file $ABI_TESTS/tutorial/Input/tspin_3.abi to Work_spin.
# Added by runtests.py output_file = "tspin_3.abo" indata_prefix = "tspin_3i" outdata_prefix = "tspin_3o" tmpdata_prefix = "tspin_3t" # end runtests.py section # Fe fcc structure with two atoms per unit cell for test of antiferromagnetic # This is the simplest fcc structure compatible with a X point spiral ecut 25.0 # SCF: nstep 70 tolwfr 1.0d-7 # Multidataset: ndtset 3 ngkpt1 4 4 2 prtdos1 1 ngkpt2 3 3 2 iscf2 -3 getden2 1 prtdos2 3 natsph2 1 iatsph2 1 ratsph2 2.4 ngkpt3 3 3 2 getden3 1 iscf3 -3 prtdos3 3 natsph3 1 iatsph3 2 ratsph3 2.4 # Crystal cell definition: natom 2 ntypat 1 znucl 26 typat 1 1 xred 0.0 0.0 0.0 0.5 0.0 0.5 acell 3*6.60 rprim 0.5 -0.5 0.0 0.5 0.5 0.0 0.0 0.0 1.0 # Magnetism: nsppol 2 spinat 0.0 0.0 4.0 0.0 0.0 -4.0 # Electron occupation: nband 20 occopt 3 tsmear 0.001 # Printing: prtden 1 prtkpt 1 # Pseudo: pp_dirpath "$ABI_PSPDIR" pseudos "Pseudodojo_nc_sr_04_pw_standard_psp8/Fe.psp8" ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tspin_3.abo, tolnlines = 0, tolabs = 0.000e+00, tolrel = 0.000e+00 #%% [paral_info] #%% max_nprocs = 4 #%% [extra_info] #%% authors = Unknown #%% keywords = NC #%% description = #%% Fe fcc structure with two atoms per unit cell for test of antiferromagnetic #%% This is the simplest fcc structure compatible with a X point spiral #%% topics = ElecDOS, AtomCentered #%%<END TEST_INFO>
You can run the calculation with this is input file and look at it to understand its contents.
Note the values of spinat. In this job, we will again characterize the magnetic structure. We are going to use atom and angular momentum projected densities of state. These are DOS weighted by the projection of the wave functions on angular momentum channels (i.e. the spherical harmonics) centered on each atom of the system. Note that these DOS are computed with the tetrahedron method, which is rather time consuming and produces more accurate but less smooth DOS than the smearing method. The CPU time is strongly dependent on the number of k-points, and we use here only a reduced set. (This will take about 40 seconds on a modern computer)
To specify this calculation we need new variables, in addition to prtdos set now to 3:
This will specify the atoms around which the calculation will be performed, and the radius of the sphere. We specifically select a new dataset for each atom, a non self-consistent calculation being run to generate the projected density of states. First, we note that the value of the total energy is -2.4972993185E+02 Ha, which shows that we have attained essentially the same state as in tspin2 (etotal=-2.4972993198E+02).
The density of states will be in the files tspin_3o_DS2_DOS_AT0001 for the first atom, and tspin_3o_DS3_DOS_AT0002 for the second atom. We can extract the density of d states, which carries most of the magnetic moment and whose integral up to the Fermi level will yield an estimate of the magnetization on each atom. We note the Fermi level (echoed in the file tspin_3o_DS1_DOS):
Fermi energy : 0.52472131
If we have a look at the integrated site-projected density of states, we can compute the total moment on each atom. To this end, one can open the file tspin_3o_DS3_DOS_AT0002, which contains information pertaining to atom 2. This file is self-documented, and describes the line content, for spin up and spin down:
# energy(Ha) l=0 l=1 l=2 l=3 l=4 (integral=>) l=0 l=1 l=2 l=3 l=4
If we look for the lines containing an energy of “0.52450”, we find
up : 0.52450 0.3714 1.0151 13.6555 0.1144 0.0683 1.29 3.30 2.49 0.05 0.02
down : 0.52450 0.1597 1.6758 9.8137 0.0872 0.0750 1.29 3.32 3.69 0.04 0.01
There are apparently changes in the DOS for all projected orbitals, but only the d orbital projection has sizeable differences. This is confirmed by looking at the integrated DOS which is different only for the d-channel. The difference between up and down is 1.20, in rough agreement (regarding our very crude methods of integration) with the previous calculation. Using a calculation with the same number of k-points for the projected DOS, we can plot the up-down integrated dos difference for the d-channel of each atom:
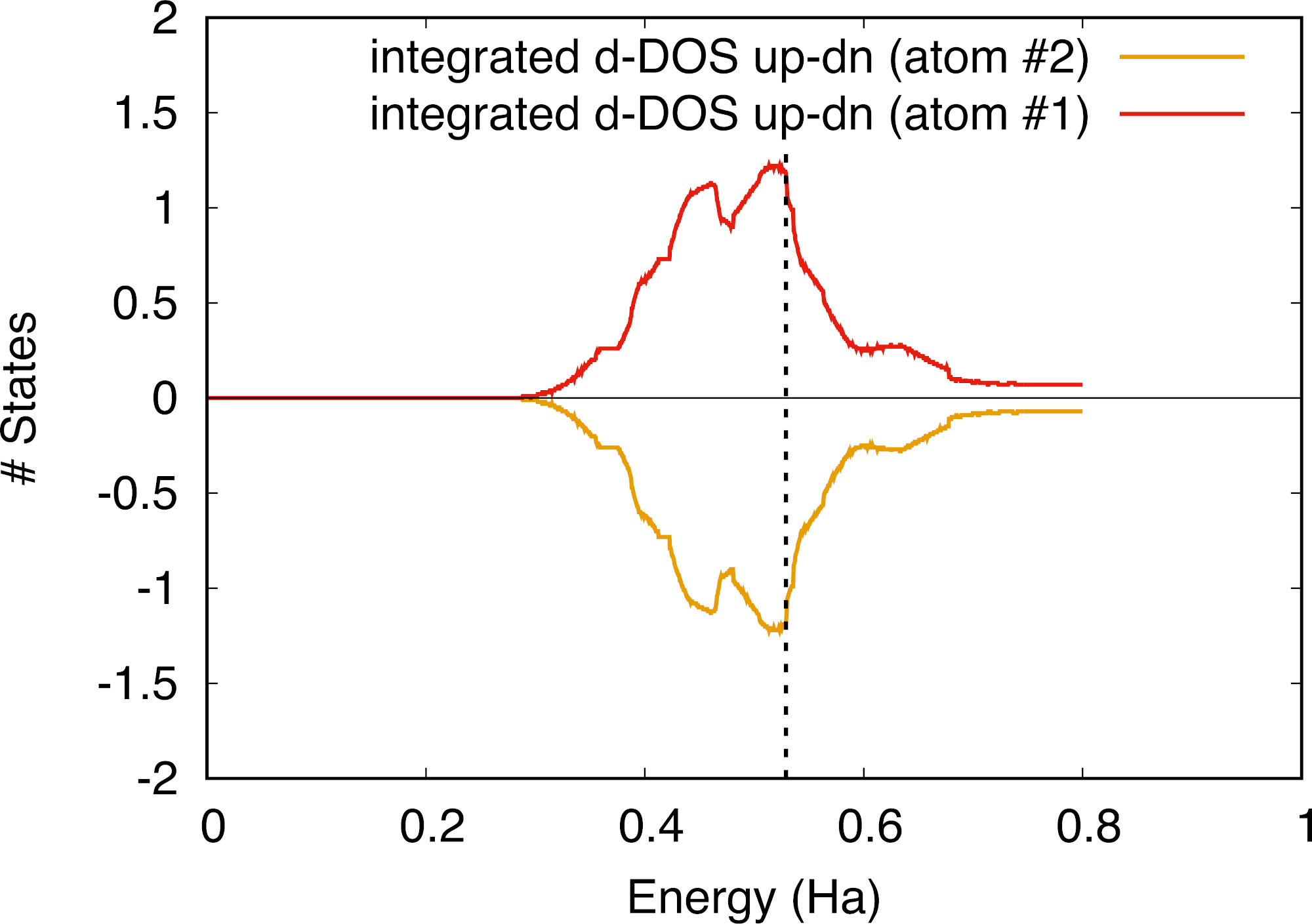
Note that there is some scatter in this graph, due to the finite number of digits of the integrated DOS given in the file tspin_3o_DS3_DOS_AT0001 and tspin_3o_DS3_DOS_AT0002. If we now look at the up and down DOS for each atom, we can see that the corner atom and the face atom possess opposite magnetizations, which roughly cancel each other. The DOS computed with the tetrahedron method is not as smooth as by the smearing method, and a running average allows for a better view.
4 Ferrimagnetic (not yet)¶
Some materials can display a particular form of ferromagnetism, which also can be viewed as non compensated antiferromagnetism, called ferrimagnetism. Some atoms possess up spin and other possess down spin, but the total spin magnetization is non zero. This happens generally for system with different type of atoms with different magnetic moment, and sometimes in rather complicated structures such as magnetite.
5 The spin-orbit coupling (SOC)¶
For heavy atoms a relativistic description of the electronic structure becomes necessary, and this can be accomplished through the relativistic DFT approach.
5.1 Norm-conserving pseudo-potentials¶
For atoms, the Dirac equation is solved and the 2(2l+1) l-channel degeneracy is lifted according to the eigenvalues of the L+S operator (l+½ and l-½ of degeneracy 2l+2 and 2l). After pseudization, the associated wave functions can be recovered by adding to usual pseudo-potential projectors a spin-orbit term of the generic form v(r).|l,s\rangle L.S \langle l,s|. Not all potentials include this additional term, if you use the pseudopotentials from pseudodojo, you have to choose those generated in a fully relativistic option (with “FR” in the name, “SR” means semi-relativistic).
In a plane wave calculation, the wavefunctions will be two-component spinors, that is they will have a spin-up and a spin-down component, and these components will be coupled. This means the size of the Hamiltonian matrix is quadrupled and the CPU time will be enlarged.
We will consider here a heavier atom than Iron: Tantalum.
You can copy the file $ABI_TESTS/tutorial/Input/tspin_5.abi in Work_spin and run the calculation.
# Single Ta atom in a big box (BCC), treated with spin-orbit coupling. enunit 2 ndtset 2 # First dataset : scalar wavefunctions # Second dataset : spinor wavefunctions nspinor2 2 # cutoff, k-points: ecut 10 nkpt 1 istwfk 1 kptopt 0 # Enter the k points manually kpt 0.0 0.0 0.0 # Crystal cell definition: natom 1 ntypat 1 znucl 73.0 typat 1 xred 0.0 0.0 0.0 acell 3*15.00 rprim 0.5 0.5 -0.5 -0.5 0.5 0.5 0.5 -0.5 0.5 # SCF: toldfe 1.0d-7 nline 5 nstep 10 # Electron occupation: nband 26 occopt 7 tsmear 0.01 # Pseudo: pp_dirpath "$ABI_PSPDIR" pseudos "Pseudodojo_nc_fr_04_pbe_standard_psp8/Ta.psp8" ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tspin_5.abo, tolnlines = 10, tolabs = 2.0e-8, tolrel = 8.0e-5 #%% [paral_info] #%% max_nprocs = 1 #%% [extra_info] #%% authors = Unknown #%% keywords = NC #%% description = Single Ta atom in a big box (BCC), treated with spin-orbit coupling. #%%<END TEST_INFO>
The input file contains one new variable:
Have a look at it. You should also look at so_psp; it is not set explicitly here, because the SO information is directly read from the pseudopotential file. One could force a non-SO calculation by setting so_psp to 0 even if the pseudo is “FR”.
In this run, we check that we recover the splitting of the atomic levels by performing a calculation in a big box. Two calculations are launched with and without SOC.
We can easily follow the symmetry of the different levels of the non-SOC calculation:
kpt# 1, nband= 26, wtk= 1.00000, kpt= 0.0000 0.0000 0.0000 (reduced coord)
-2.60792 -1.43380 -1.43380 -1.43380 -0.14851 -0.09142 -0.09142 -0.09142
-0.09033 -0.09033 0.02657 0.02657 0.02657 0.05604 0.14930 0.14930
0.14930 0.15321 0.15321 0.15321 0.16211 0.16211 0.27952 0.27952
0.27952 0.31238
That is, the symmetry: s, p, s, d After application of the SOC, we now have to consider twice as many levels:
kpt# 1, nband= 26, wtk= 1.00000, kpt= 0.0000 0.0000 0.0000 (reduced coord)
-2.59704 -2.59704 -1.65268 -1.65268 -1.32544 -1.32544 -1.32544 -1.32544
-0.14663 -0.14663 -0.09760 -0.09760 -0.09760 -0.09760 -0.07881 -0.07881
-0.07805 -0.07805 -0.07805 -0.07805 0.01044 0.01044 0.03597 0.03597
0.03597 0.03597
The levels are not perfectly degenerate, due to the finite size of the simulation box, and in particular the cubic shape, which gives a small crystal field splitting of the d orbitals between e_g and t_{2g} states. We can nevetheless compute the splitting of the levels, and we obtain, for e.g. the p-channel: 1.65268-1.32544=0.32724 Ha
If we now consider the NIST table of atomic data, we obtain:
5p splitting, table: 1.681344-1.359740 = 0.321604 Ha
5d splitting, table: 0.153395-0.131684 = 0.021711 Ha
We obtain a reasonable agreement. A better agreement could be obtained by improving the convergence parameters.
5.2 Projector Augmented-Wave¶
Within the Projector Augmented-Wave (PAW) method, the usual (pseudo-)Hamiltonian can be expressed as:
If the two following conditions are satisfied:
(1) the local PAW basis is complete enough; (2) the electronic density is mainly contained in the PAW augmentation regions,
it can be shown that a very good approximation of the PAW Hamiltonian – including spin-orbit coupling – is:
where D^{SO}_{ij} is the projection of the (L.S) operator into the PAW augmentation regions. As an immediate consequence, we have the possibility to use the standard p_i PAW projectors; in other words, it is possible to use the standard PAW datasets (pseudopotentials) to perform calculations including SOC. But, of course, it is still necessary to express the wave-functions as two components spinors (spin-up and a spin-down components). Let’s have a look at the following keyword:
This activates the spin-orbit coupling within PAW (forcing nspinor=2).
Now the practice: We consider Bismuth, the PAW dataset file contains the 5d, 6s and 6p electrons in the valence.
You can copy the file $ABI_TESTS/tutorial/Input/tspin_6.abi in Work_spin (one Bismuth atom in a large cell) and run the calculation. It takes about 10 seconds on a recent computer.
# Isolated Bi atom ndtset 2 pawspnorb1 0 ! Without spin-orbit pawspnorb2 1 ! With spin-orbit nsym 1 # cutoff, k-points: kptopt 4 ecut 8 pawecutdg 15 # Crystal cell definition: natom 1 ntypat 1 typat 1 znucl 83.d0 xred 3*0.0 acell 3*10 #This parameter is of course for testing purposes only # electron occupation: occopt 7 tsmear 0.02 nband1 12 nband2 24 # 2 times more band with SOC # SCF: nstep 20 toldfe 1.0d-7 # Pseudo: pp_dirpath "$ABI_PSPDIR" pseudos "Pseudodojo_paw_pw_standard/Bi.xml" ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tspin_6.abo, tolnlines= 5, tolabs= 3.000e-08, tolrel= 3.000e-03 #%% [paral_info] #%% max_nprocs = 1 #%% [extra_info] #%% authors = Unknown #%% keywords = PAW #%% description = #%% Bismuth atom, isolated, in a supercell - with and without spin-orbit coupling. #%%<END TEST_INFO>
Two datasets are executed: the first without SOC, the second one using pawspnorb=1.
The resulting eigenvalues are:
Without SOC:
Eigenvalues (hartree) for nkpt= 1 k points:
kpt# 1, nband= 12, wtk= 1.00000, kpt= 0.0000 0.0000 0.0000 (reduced coord)
5d -0.86985 -0.86985 -0.86879 -0.86879 -0.86879
6s -0.43169
6p -0.05487 -0.05486 -0.05486
...
With SOC:
kpt# 1, nband= 24, wtk= 1.00000, kpt= 0.0000 0.0000 0.0000 (reduced coord)
5d -0.91225 -0.91225 -0.91225 -0.91225 -0.80130 -0.80130 -0.80130 -0.80130 -0.80062 -0.80062
6s -0.41697 -0.41697
6p -0.09644 -0.09644 -0.02639 -0.02639 -0.02639 -0.02639
...
Again, the levels are not perfectly degenerate, due to the finite size and non spherical shape of the simulation box. We can compute the splitting of the levels, and we obtain:
5d-channel: 0.91225-0.80062 = 0.11163 Ha
6p-channel: 0.09644-0.02639 = 0.07005 Ha
If we now consider the NIST table of atomic data, we obtain:
5d-channel: 1.063136-0.952668 = 0.11047 Ha
6p-channel: 0.228107-0.156444 = 0.07166 Ha
A perfect agreement even with a small simulation cell and very small values of plane-wave cut-offs. This comes from the generation of the PAW dataset, where the SOC is calculated very accurately and for an atomic reference. The exchange correlation functional has little impact on large SOC splittings, which are mainly a kinetic energy effect.
6 Rotation of the magnetization and spin-orbit coupling (coming soon)¶
The most spectacular manifestation of the SOC is the energy associated with a rotation of the magnetisation with respect to the crystal axis. It is at the origin of the magneto crystalline anisotropy (MCA) of paramount technological importance.
7 Summary¶
The table below can help to know how to handle the different magnetic calculation cases in ABINIT:
| case | nsppol | nspinor | nspden |
|---|---|---|---|
| non-magnetic | 1 | 1 | 1 |
| collinear FM | 2 | 1 | 2 |
| collinear AFM | 1 | 1 | 2 |
| non-collinear | 1 | 2 | 4 |
Note that non-collinear magnetism can be done with or without SOC. With SOC do not use time reversal symmetry (kptopt = 4), however as the symmetries in the presence of SOC it is not (yet fully) implemented please remove all symmetries when running non-collinear magnetism with SOC (i.e. kptopt=3 and nsym=1). The non-collinear magnetism + SOC cases can be much more difficult to converge (SCF) and might require to strongly reduce the diemix and mostly the diemixmag mixing flags; you might have to increase nline and play with negative values of nnsclo. DFT+U correction is also necessary in most of the magnetic calculations if you use regular LDA and GGA functionals (i.e. not hybrid fucntionals).
GZ would like to thank B. Siberchicot for useful comments.