Tutorial on optical properties¶
Frequency-dependent linear and second-order nonlinear optical response.¶
This tutorial aims at showing how to get the following physical properties, for semiconductors:
- Frequency-dependent linear dielectric tensor
- Frequency-dependent second-order nonlinear susceptibility tensor
- Frequency-dependent electro-optical susceptibility tensor
in the simple Random-Phase Approximation or Sum-over-states approach. This tutorial will help you to understand and make use of optic. Before starting, you should first have some theoretical background. We strongly suggest that you first read the first two sections of the optic help file.
This tutorial should take about 1 hour.
Note
Supposing you made your own installation of ABINIT, the input files to run the examples are in the ~abinit/tests/ directory where ~abinit is the absolute path of the abinit top-level directory. If you have NOT made your own install, ask your system administrator where to find the package, especially the executable and test files.
In case you work on your own PC or workstation, to make things easier, we suggest you define some handy environment variables by executing the following lines in the terminal:
export ABI_HOME=Replace_with_absolute_path_to_abinit_top_level_dir # Change this line
export PATH=$ABI_HOME/src/98_main/:$PATH # Do not change this line: path to executable
export ABI_TESTS=$ABI_HOME/tests/ # Do not change this line: path to tests dir
export ABI_PSPDIR=$ABI_TESTS/Pspdir/ # Do not change this line: path to pseudos dir
Examples in this tutorial use these shell variables: copy and paste
the code snippets into the terminal (remember to set ABI_HOME first!) or, alternatively,
source the set_abienv.sh script located in the ~abinit directory:
source ~abinit/set_abienv.sh
The ‘export PATH’ line adds the directory containing the executables to your PATH so that you can invoke the code by simply typing abinit in the terminal instead of providing the absolute path.
To execute the tutorials, create a working directory (Work*) and
copy there the input files of the lesson.
Most of the tutorials do not rely on parallelism (except specific tutorials on parallelism). However you can run most of the tutorial examples in parallel with MPI, see the topic on parallelism.
Computing the momentum matrix elements¶
Before beginning, you might consider working in a different subdirectory. Why not create Work_optic?
We also need to copy toptic_1.abi from $ABI_TESTS/tutorial/Input to Work_optic.
cd $ABI_TESTS/tutorespfn/Input
mkdir Work_optic
cd Work_optic
cp ../toptic_1.abi .
Now, you are ready to run Abinit and prepare the files needed for Optic. Issue:
abinit toptic_1.abi > log 2> err
We now examine the input file.
# Prepare the computation of linear and non-linear optic properties # of GaAs crystal : ground-state with few bands, # then non-SCF with a larger number of bands, then ddk for different directions # Note that the k point sampling shoud be finer for significant results. The cut-off energy is also too low. ndtset 6 #First dataset : SC run with kpoints in the IBZ nband1 4 nstep1 25 kptopt1 1 nbdbuf1 0 prtden1 1 getden1 0 getwfk1 0 # Usual file handling data #Second dataset : NSC run with large number of bands, and points in the IBZ iscf2 -2 nstep2 25 kptopt2 1 getwfk2 1 getden2 1 # Usual file handling data #Third dataset : NSC run with large number of bands, and points in the full BZ iscf3 -2 nstep3 25 getwfk3 2 getden3 1 # Usual file handling data #Fourth dataset : ddk response function along axis 1 iscf4 -3 nstep4 1 nline4 0 prtwf4 3 # Speed up the calculation : the first-order response wavefunction is not computed, only the matrix elements. nqpt4 1 rfdir4 1 0 0 rfelfd4 2 #Fifth dataset : ddk response function along axis 2 iscf5 -3 nstep5 1 nline5 0 prtwf5 3 # Speed up the calculation : the first-order response wavefunction is not computed, only the matrix elements. nqpt5 1 rfdir5 0 1 0 rfelfd5 2 #Sixth dataset : ddk response function along axis 3 iscf6 -3 nstep6 1 nline6 0 prtwf6 3 # Speed up the calculation : the first-order response wavefunction is not computed, only the matrix elements. nqpt6 1 rfdir6 0 0 1 rfelfd6 2 # Data common to datasets 2-6 nband 20 # This number of bands might be too low for non-linear optics and real part of linear optics # Data common to datasets 3-6 kptopt 3 # Need points in the full BZ for non-linear optical properties # Data common to datasets 4-6 getwfk 3 #Data common to all datasets nshiftk 4 shiftk 0.5 0.5 0.5 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.5 ngkpt 4 4 4 # This is much too low : should be at least 24x24x24 qpt 0.0 0.0 0.0 # Not really needed, because it is the defaults, but mentioned here to keep track of its importance for datasets 4-6 acell 3*10.60 diemac 10.0 ecut 2.00 # This is also too low natom 2 nbdbuf 2 ntypat 2 rprim 0 .5 .5 .5 0 .5 .5 .5 0 xred 3*0.00d0 3*0.25d0 typat 1 2 tolwfr 1.e-20 znucl 31 33 pp_dirpath "$ABI_PSPDIR" pseudos "Psdj_nc_sr_04_pw_lrgcore_psp8/Ga-low.psp8, Psdj_nc_sr_04_pw_lrgcore_psp8/As.psp8" ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% test_chain = toptic_1.abi, toptic_2.abi #%% need_cpp_vars = !HAVE_MPI_IO_DEFAULT #%% [files] #%% files_to_test = #%% toptic_1.abo, tolnlines= 0, tolabs= 0.000e+00, tolrel= 0.000e+00, fld_options = -easy #%% [paral_info] #%% max_nprocs = 2 #%% [extra_info] #%% authors = S. Sharma, X. Gonze #%% keywords = NC, DFPT #%% description = #%% Prepare the computation of linear and non-linear optic properties #%% of GaAs crystal: ground-state with few bands, #%% then non-SCF with a larger number of bands, then ddk for different directions #%% Note that the k point sampling shoud be finer for significant results. The cut-off energy is also too low. #%%<END TEST_INFO>
The computation concerns a crystal of GaAs, in the zinc-blende structure (2 atoms per primitive cell). It has six datasets.
The first dataset is a quite standard self-consistent determination of the ground state for a fixed geometry. Only the occupied bands are treated. The density is output and used in later datasets.
The second dataset is a non-self-consistent calculation, where the number of bands has been increased to include unoccupied states. The k points are restricted to the Irreducible Brillouin Zone.
The third dataset uses the result of the second one to produce the wavefunctions for all the bands, for the full Brillouin Zone (this step could be skipped for linear optic, but is included for later CPU time saving - for nonlinear optic, checks of symmetry behaviour are ongoing currently as of 23 June 2024, better to perform set three). If only the linear optical response is computed, then time-reversal symmetry can be used, and the computation might be restricted to the half Brillouin zone (kptopt=2).
The fourth, fifth, and sixth datasets correspond to the computation of the ddk matrix elements, that is, matrix elements of the \(\partial H / \partial k\) operators where \(H\) is the Hamiltonian. Note that the number of bands is the same as for datasets 2 and 3. Note also that these are non-self-consistent calculations, moreover, restricted to nstep = 1 and nline = 0. Indeed, only the matrix elements between explicitly computed (unperturbed) states are required. This also is why prtwf=3 is used. Using a larger nstep would lead to a full computation of the derivative of the wavefunction with respect to the wavevector, while in Optic, only the matrix elements between unperturbed states are needed. Thus a value of nstep larger than one would be a waste of time.
A useful alternative is to use wfk_task=”wfk_optics_fullbz” after the calculation of the WFK file for just the irreducible Brillouin zone: this postprocessing step calculates the matrix elements needed for optic, and is much more memory efficient.
In order to have a sufficiently fast tutorial, the k point sampling was chosen to be extremely dense. Instead of a \(4\times 4\times 4\) FCC lattice (256 k points), it should be something like \(28\times 28\times 28\) FCC (about 100000 k points). Also, the cut-off energy (2 Ha) is too small. As usual, convergence studies are the responsibility of the user. Moreover, we emphasize that in general the results of a sum-over-states approach, as is used in Optic, typically converges quite slowly with the k point mesh. Thus it is of uttermost importance to test convergence carefully.
The run takes less than one minute on a 2.8 GHz PC. The files toptic_1o_DS3_WFK, toptic_1o_DS4_1WF7, toptic_1o_DS5_1WF8 and toptic_1o_DS6_1WF9 are the four files requested for the Optic run. The first file contains the wavefunctions for the filled and empty states in the entire Brillouin zone, while the latter three contain the matrix elements of the \(\partial/\partial k\) operators, one file for each Cartesian direction.
Real preparation runs (with adequate k point sampling and cut-off energy) can last several hours (or even days) on such a PC.
Computing the linear and nonlinear optical response¶
The next step is to compute the linear and nonlinear optical response: once the momentum matrix elements are available, you are ready to determine the optical response (up to second order in the current implementation) for the material under study.
First, read the section 3 of the Optic help file.
Copy the toptic_2.abi input file from $ABI_TESTS/tutorial/Input to Work_optic:
cp ../toptic_2.abi .
The toptic_2.abi is your input file. You should edit it and read it carefully. For help on various input parameters in this file, please see the optic help file.
&FILES ddkfile_1 = 'toptic_1o_DS4_1WF7', ddkfile_2 = 'toptic_1o_DS5_1WF8', ddkfile_3 = 'toptic_1o_DS6_1WF9', wfkfile = 'toptic_1o_DS3_WFK' / &PARAMETERS broadening = 0.002, domega = 0.0003, maxomega = 0.3, scissor = 0.000, tolerance = 0.002 / &COMPUTATIONS num_lin_comp = 1, lin_comp = 11, num_nonlin_comp = 2, nonlin_comp = 123,222, num_linel_comp = 0, num_nonlin2_comp = 0, / ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = optic #%% test_chain = toptic_1.abi, toptic_2.abi #%% need_cpp_vars = !HAVE_MPI_IO_DEFAULT #%% [files] #%% files_to_test = #%% toptic_2_0001_0001-linopt.out, tolnlines= 0, tolabs= 0.000e+00, tolrel= 0.000e+00, fld_options = -easy; #%% toptic_2_0001_0002_0003-ChiTotRe.out, tolnlines= 16, tolabs= 7.000e-04, tolrel= 7.000e-04, fld_options = -easy; #%% toptic_2_0001_0002_0003-ChiTotIm.out, tolnlines= 16, tolabs= 4.000e-04, tolrel= 2.000e-04, fld_options = -easy #%% [paral_info] #%% max_nprocs = 4 #%% [extra_info] #%% authors = S. Sharma, X. Gonze #%% keywords = #%% description = Input file for optic code. #%%<END TEST_INFO>
When you have read the input file, you can run the code, as usual, using the following command (assuming optic is in $PATH - copy the executable in the current directory if needed):
optic toptic_2.abi > log 2> err &
It will take a few seconds to run. You have produced numerous output files. Now, you can examine some of these output files.
The headers contains information about the calculation. See the section 4 of the Optic help file. These files can be plotted in xmgrace or gnuplot . If you do not have xmgrace installed on your computer, please get it from the Web, and install it, or alternatively, use your preferred plotting package.
We will first have a look at the linear optic file.
xmgrace toptic_2_0001_0001-linopt.out
This file contains the xx component of the dielectric tensor, and includes, as a function of energy, the magnitude, real, and imaginary parts of the tensor element. On the graph, you should see three curves. One of them is positive, and always larger than the two others. It is the modulus of the dielectric function. Another one is also always positive, it is the imaginary part of the dielectric function. The last one is the real part. There are a large number of peaks. This is at variance with the experimental spectra, which are much smoother. The origin of this discrepancy is to be found in the very sparse k point sampling that we used in order to be able to perform the tutorial quickly. In the next section, we will improve this sampling, and start a convergence study.
Concerning the non-linear optics, the graphs for the xyz components are also quite bad, with many isolated (but broadened) peaks. However, the yyy ones are perfect. Indeed, they vanish due to symmetry reasons! Visualize the imaginary part with:
xmgrace toptic_2_0002_0002_0002-ChiTotIm.out
and the Real part with:
xmgrace toptic_2_0002_0002_0002-ChiTotRe.out
Tip
If AbiPy is installed on your machine, you can use the abiopen.py script
with the --expose option to visualize the results stored in the OPTIC.nc file:
abiopen.py toptic_2_OPTIC.nc --expose -sns=paper
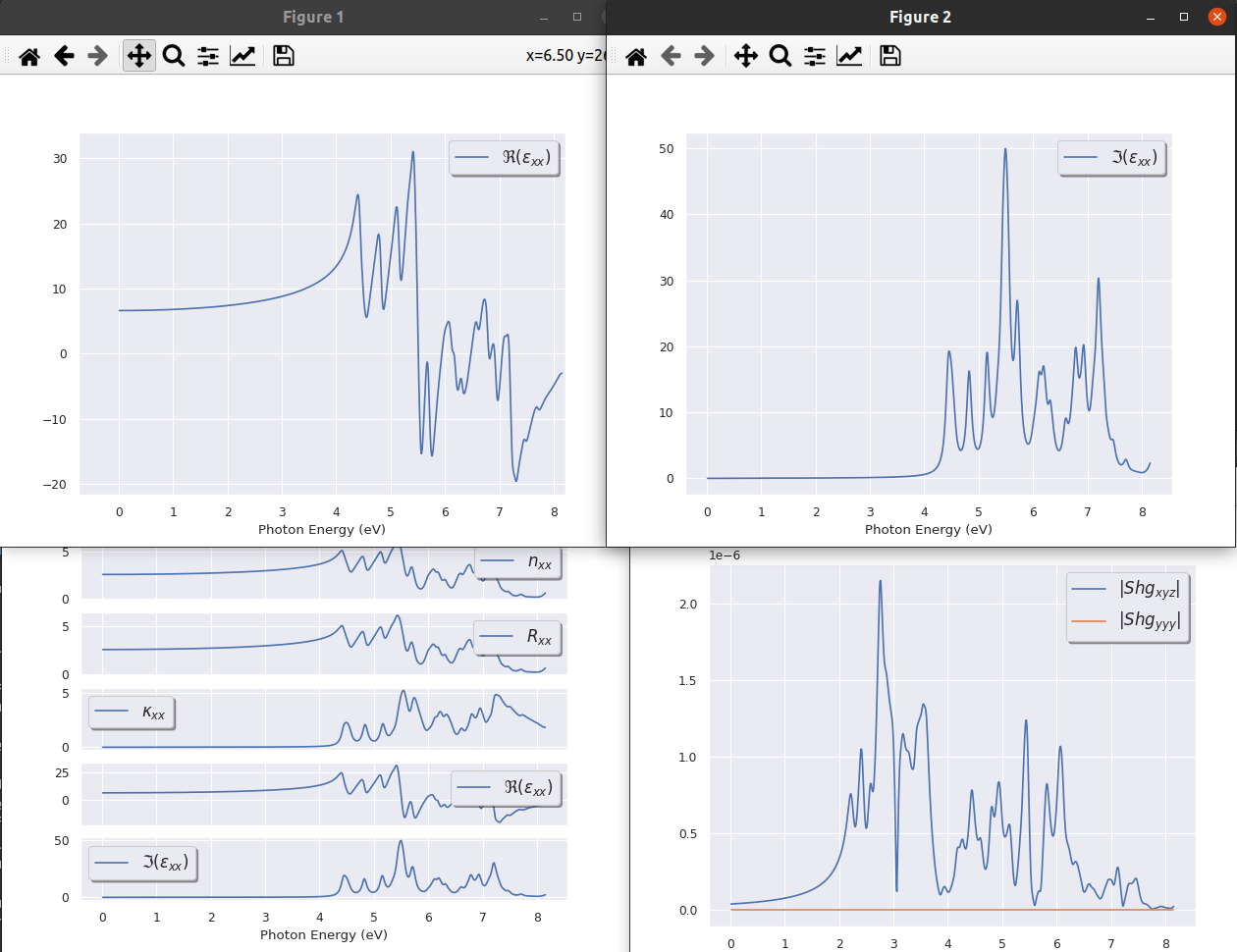
This would be a good time to review section 5 of the optic help file.
For comparison, we have included in the tutorial directory of the ABINIT package (ask your administrator to have access to the full ABINIT package if you do not have your own installation), three files that have been obtained with a much better k point sampling (still with a low cut-off energy and a number of bands that should be larger). You can visualize them as follows:
xmgrace $ABI_HOME/doc/tutorial/optic_assets/toptic_ref_0001_0001-linopt.out
for the linear optics, obtained with a 28x28x28 grid (keeping everything else fixed), and
xmgrace $ABI_HOME/doc/tutorial/optic_assets/toptic_ref_0001_0002_0003-ChiTotIm.out
as well as
xmgrace $ABI_HOME/doc/tutorial/optic_assets/toptic_ref_0001_0002_0003-ChiTotRe.out
for the non-linear optics, obtained with a 18x18x18 grid (keeping everything else fixed).
Concerning the linear spectrum, we will now compare this (underconverged) result toptic_ref_0001_0001-linopt.out with experimental data and converged theoretical results.
The book by Cohen M.L. and Chelikowsky [Cohen1988] presents a comparison of experimental data with the empirical pseudopotential method spectrum. If you do not have access to this book, you can see an experimental spectrum in [Philipp1963], and a theoretical spectrum in [Huang1993], as well as other sources.
We discuss first the imaginary spectrum. Prominent experimental features of this spectrum are two peaks located close to 3 eV and 5 eV, both with the same approximate height. The spectrum is zero below about 1.5 eV (the direct band gap), and decreases with some wiggles beyond 5.5 eV. Converged theoretical spectra also show two peaks at about the same location, although their heights are markedly different: about 10 for the first one (at 3 eV), and 25 for the second one (at 5 eV). Other features are rather similar to the experimental ones. In the linear optic spectrum of toptic_ref_0001_0001-linopt.out, we note that there is a shoulder at around 3 eV, and a peak at 4.2 eV, with respective approximate heights of 7 and 25. Some comments are in order:
-
The main difference between experimental and converged theoretical spectra is due to the presence of excitons (electron-hole bound states), not treated at all in this rather elementary theoretical approach: excitons transfer some oscillator strength from the second peak (at 5 eV) to the first one (at 3 eV). Going beyond the Sum-Over-State approach, but still keeping the independent-electron approximation, e.g., in the framework of the TDDFT (adiabatic LDA) will not correct this problem. One needs to use the Bethe-Salpeter approximation, or to rely on fancy exchange-correlation kernels, to produce an optical spectrum in qualitative agreement with the experimental data. Still, trends should be correct (e.g. change of the peak positions with pressure, comparison between different semiconductors, etc.).
-
In many early theoretical spectra (including the ones in [Cohen1988]), the agreement between the theoretical and experimental band gap is artificially good. In straight DFT, one cannot avoid the band gap problem. However, it is possible to add an artificial “scissor shift”, to make the theoretical band gap match the experimental one.
-
Our theoretical spectrum presents additional deficiencies with respect to the other ones, mostly due to a still too coarse sampling of the k space (there are too many wiggles in the spectrum), and to a rather inaccurate band structure (the cut-off energy was really very low, so that the first peak only appears as a shoulder to the second peak).
The real part of the spectrum is related by the Kramers-Kronig relation to the imaginary part. We note that the deficiencies of the imaginary part of the spectrum translate to the real part: the first peak is too low, and the second peak too high, while the spectrum correctly changes sign around 5 eV, and stays negative below 8 eV.
In our simulation, more empty states are needed to obtain a better behaviour. Also, the limiting low-frequency value is only 4.3, while it should be on the order of 10. This can be corrected by increasing the cut-off energy, the k point sampling and the number of unoccupied states.
Similar considerations apply to the non-linear spectra.
Faster computation of the imaginary part of the linear optical response¶
In the case of the imaginary part of the linear optical response, there are several points that make the calculation easier:
-
The time-reversal symmetry can be used to decrease the number of k points by a factor of two (this is also true for the computation of the real spectrum);
-
The number of unoccupied bands can be reduced to the strict minimum needed to span the target range of frequencies.
We will focus on the energy range from 0 eV to 8 eV, for which only 5 unoccupied bands are needed.
Copy the input file toptic_3.abi in Work_optic:
cp ../toptic_3.abi .
# Prepare the computation of linear optic properties # (for the imaginary spectrum only: the number of bands can be taken much lower than for the real part) # of GaAs crystal : ground-state with few bands, # then non-SCF with a larger number of bands, then ddk for different directions # Note that the k point sampling shoud be finer for significant results. The cut-off energy is also too low. # Use of TRS to compute less kpts and use less bands # Data common to datasets 2-6 nband 9 # Minimal number of bands for linear optics (imaginary part of the spectrum) # Data common to datasets 3-6 kptopt 2 # Need points in the half BZ (use time-reversal symmetry) #------------------------------------------------------------------------------- #The rest of this file is similar to the toptic_1.abi file, except #that nband and kptopt have been moved above ... ndtset 6 #First dataset : SC run with kpoints in the IBZ nband1 4 nstep1 25 kptopt1 1 nbdbuf1 0 prtden1 1 getden1 0 getwfk1 0 # Usual file handling data #Second dataset : NSC run with large number of bands, and points in the IBZ iscf2 -2 nstep2 25 kptopt2 1 getwfk2 1 getden2 1 # Usual file handling data #Third dataset : NSC run with large number of bands, and points in the the full BZ iscf3 -2 nstep3 25 getwfk3 2 getden3 1 # Usual file handling data #Fourth dataset : ddk response function along axis 1 iscf4 -3 nstep4 1 nline4 0 prtwf4 3 # Speed up the calculation : the first-order response wavefunction is not computed, only the matrix elements nqpt4 1 rfdir4 1 0 0 rfelfd4 2 #Fifth dataset : ddk response function along axis 2 iscf5 -3 nstep5 1 nline5 0 prtwf5 3 # Speed up the calculation : the first-order response wavefunction is not computed, only the matrix elements. nqpt5 1 rfdir5 0 1 0 rfelfd5 2 #Sixth dataset : ddk response function along axis 3 iscf6 -3 nstep6 1 nline6 0 prtwf6 3 # Speed up the calculation : the first-order response wavefunction is not computed, only the matrix elements. nqpt6 1 qpt6 0.0d0 0.0d0 0.0d0 rfdir6 0 0 1 rfelfd6 2 # Data common to datasets 4-6 getwfk 3 #Data common to all datasets nshiftk 4 shiftk 0.5 0.5 0.5 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.5 ngkpt 3*4 # This is much too low : should be at least 24x24x24 acell 3*10.60 diemac 10.0 ecut 2.00 # This is also too low natom 2 nbdbuf 2 ntypat 2 rprim 0 .5 .5 .5 0 .5 .5 .5 0 xred 3*0.00d0 3*0.25d0 typat 1 2 tolwfr 1.e-20 znucl 31 33 pp_dirpath "$ABI_PSPDIR" pseudos "Psdj_nc_sr_04_pw_lrgcore_psp8/Ga-low.psp8, Psdj_nc_sr_04_pw_lrgcore_psp8/As.psp8" ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% test_chain = toptic_3.abi, toptic_4.abi, toptic_5.abi #%% need_cpp_vars = !HAVE_MPI_IO_DEFAULT #%% [files] #%% files_to_test = #%% toptic_3.abo, tolnlines= 0, tolabs= 0.000e+00, tolrel= 0.000e+00, fld_options = -easy #%% [paral_info] #%% max_nprocs = 2 #%% [extra_info] #%% authors = S. Sharma, X. Gonze #%% keywords = NC, DFPT #%% description = #%% Prepare the computation of linear optic properties (for the imaginary spectrum only) #%% of GaAs crystal: ground-state with few bands, #%% then non-SCF with a larger number of bands, then ddk for different directions #%% Note that the k point sampling shoud be finer for significant results. The cut-off energy is also too low. #%%<END TEST_INFO>
Issue:
abinit toptic_3.abi > log 2> err &
Now, examine the file toptic_3.abi. There are two important changes with respect to the file toptic_1.abi:
- the number of unoccupied bands has been reduced, so that the total number of bands is 9 instead of 20
- when applicable, the value of kptopt 3 in our previous simulation has been changed to 2, in order to take advantage of the time-reversal symmetry
When the run is finished (it is only 8 secs on a 2.8 GHz PC), you can process the WFK files and obtain the linear optic spectra. Copy the toptic_4.abi input file in Work_optic:
cp ../toptic_4.abi .
&FILES ddkfile_1 = 'toptic_3o_DS4_1WF7', ddkfile_2 = 'toptic_3o_DS5_1WF8', ddkfile_3 = 'toptic_3o_DS6_1WF9', wfkfile = 'toptic_3o_DS3_WFK' / &PARAMETERS broadening = 0.002, domega = 0.0003, maxomega = 0.3, scissor = 0.000, tolerance = 0.002 / &COMPUTATIONS num_lin_comp = 1, lin_comp = 11, num_nonlin_comp = 0, num_linel_comp = 0, num_nonlin2_comp = 0, / ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = optic #%% test_chain = toptic_3.abi, toptic_4.abi, toptic_5.abi #%% need_cpp_vars = !HAVE_MPI_IO_DEFAULT #%% [files] #%% files_to_test = #%% toptic_4_0001_0001-linopt.out, tolnlines= 0, tolabs= 0.000e+00, tolrel= 0.000e+00, fld_options = -easy #%% [paral_info] #%% max_nprocs = 4 #%% [extra_info] #%% authors = S. Sharma, X. Gonze #%% description = Input file for optic code. #%%<END TEST_INFO>
Examine toptic_4.abi file: only the linear optic spectra will be built.
When you have read the input file, you can run the code, as usual using the following command
optic toptic_4.abi > log 2> err &
Then, you can visualize the files toptic_2_0001_0001-linopt.out and toptic_4_0001_0001-linopt.out using xmgrace and compare them. The spectra looks completely identical. However, a careful look at these files, by editing them, show that indeed, the imaginary part is very similar:
#calculated the component: 1 1 of dielectric function
#broadening: 0.000000E+00 2.000000E-03
#scissors shift: 0.000000E+00
#energy window: 3.897388E+01eV 1.432264E+00Ha
# Energy(eV) Im(eps(w))
8.163415E-03 1.463528E-04
1.632683E-02 2.927094E-04
2.449025E-02 4.390740E-04
3.265366E-02 5.854504E-04
...
But the real parts differ slightly (this is seen at lines 1007 and beyond):
# Energy(eV) Re(eps(w))
8.163415E-03 6.623599E+00
1.632683E-02 6.623632E+00
2.449025E-02 6.623686E+00
3.265366E-02 6.623763E+00
...
for toptic_2_0001_0001-linopt.out and
# Energy(eV) Re(eps(w))
8.163415E-03 6.518576E+00
1.632683E-02 6.518608E+00
2.449025E-02 6.518663E+00
3.265366E-02 6.518740E+00
for toptic_4_0001_0001-linopt.out. This small difference is due to the number of bands (nband 20 for toptic_2_0001_0001-linopt.out and nband 9 for toptic_4_0001_0001-linopt.out).
Then, you can increase the number of k points, and watch the change in the imaginary part of the spectrum. There will be more and more peaks, until they merge, and start to form a smooth profile (still not completely smooth even with \(28\times 28\times 28\)). For your information, we give some timings of the corresponding Abinit run for a 2.8 GHz PC:
k-point grid CPU time
4 x 4 x 4 8 secs
6 x 6 x 6 20 secs
8 x 8 x 8 43 secs
10 x 10 x 10 80 secs
12 x 12 x 12 138 secs
16 x 16 x 16 338 secs
20 x 20 x 20 702 secs
24 x 24 x 24 1335 secs
28 x 28 x 28 2633 secs
For grids on the order of \(16\times 16\times 16\), the treatment by optics also takes several minutes, due to IO (30 minutes for the \(28\times 28\times 28\) grid). You might note how the first peak slowly develop with increasing number of k points but nevertheless stays much smaller than the converged one, and even smaller than the experimental one.
Computing the linear electro-optical susceptibility¶
Calculations of the linear electro-optical susceptibility follows the same inital calculations as those described in the first two sections of this tutorial. To calculate the coefficients of the linear electro-optical susceptibility one needs to modify the optic input file with two additional keywords.
Copy the toptic_5.abi input file in Work_optic:
cp ../toptic_5.abi .
&FILES ddkfile_1 = 'toptic_3o_DS4_1WF7', ddkfile_2 = 'toptic_3o_DS5_1WF8', ddkfile_3 = 'toptic_3o_DS6_1WF9', wfkfile = 'toptic_3o_DS3_WFK' / &PARAMETERS broadening = 0.002, domega = 0.0003, maxomega = 0.3, scissor = 0.000, tolerance = 0.002 / &COMPUTATIONS num_lin_comp = 0, lin_comp = 0, num_nonlin_comp = 0 nonlin_comp = 0, num_linel_comp = 1, linel_comp = 123, / ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = optic #%% test_chain = toptic_3.abi,toptic_4.abi,toptic_5.abi #%% need_cpp_vars = !HAVE_MPI_IO_DEFAULT #%% [files] #%% files_to_test = #%% toptic_5_0001_0002_0003-ChiEOAbs.out, tolnlines= 16, tolabs= 7.000e-04, tolrel= 7.000e-04, fld_options = -easy; #%% toptic_5_0001_0002_0003-ChiEOIm.out, tolnlines= 16, tolabs= 7.000e-04, tolrel= 7.000e-04, fld_options = -easy; #%% toptic_5_0001_0002_0003-ChiEORe.out, tolnlines= 16, tolabs= 7.000e-04, tolrel= 7.000e-04, fld_options = -easy; #%% toptic_5_0001_0002_0003-ChiEOTotIm.out, tolnlines= 16, tolabs= 7.000e-04, tolrel= 7.000e-04, fld_options = -easy; #%% toptic_5_0001_0002_0003-ChiEOTotRe.out, tolnlines= 16, tolabs= 7.000e-04, tolrel= 7.000e-04, fld_options = -easy; #%% [paral_info] #%% max_nprocs = 4 #%% [extra_info] #%% authors = S. Sharma, X. Gonze, N. A. Pike #%% keywords = linear-electro-optical #%% description = Input file for optic code to calculate the linear electro-optical coefficient #%%<END TEST_INFO>
For toptic_5.abi, only the linear electro-optic susceptibility will be calculated.
When you have read the input file, you can run the code, as usual using the following command
optic toptic_5.abi > log 2> err &
The calculation should run in a few seconds on a modern PC.
The resulting calculation produces a number of files ending in ChiEO and are related to different parts of the linear electro-optical tensor:
- ChiEOAbs.out gives the absolute value of the linear electro-optical susceptibility
- ChiEOIm.out gives the imaginary components of the calculated linear electro-optical susceptibility
- ChiEORe.out gives the real components of the calculated linear electro-optical susceptibility
- ChiEOTotIm.out gives the total imaginary part of the calculated linear electro-optical susceptibility
- ChiEOTotRe.out gives the total real part of the calculated linear electro-optical susceptibility
Generally, the low energy (or frequency) range of the linear electro-optical susceptibility is linear and of experimental importance. Here, low energy means energies much less than the band gap energy.