Polarization and finite electric fields

Polarization, and responses to finite electric fields for AlP.

This tutorial describes how to obtain the following physical properties, for an insulator:

• The polarization.
• The Born effective charge (by finite differences of polarization)
• The Born effective charge (by finite differences of forces)
• The dielectric constant
• The proper piezoelectric tensor (clamped and relaxed ions)

The case of the linear responses (for the Born effective charge, dielectric constant, piezoelectric tensor) is treated independently in other tutorials (Response-Function 1, Elastic properties), using Density-Functional Perturbation Theory. You will learn here how to obtain these quantities using finite difference techniques within ABINIT. To that end, we will describe how to compute the polarization, in the Berry phase formulation, and how to perform finite electric field calculations.

The basic theory for the Berry phase computation of the polarization was proposed by R. D. King-Smith and D. Vanderbilt in [Kingsmith1993]. The longer excellent paper by D. Vanderbilt and R. D. King-Smith ([Vanderbilt1993]) clarifies many aspects of this theory. Good overviews of this subject may be found in the review article [Resta1994] and book [Vanderbilt2018].

In order to gain the theoretical background needed to perform a calculation with a finite electric field, you should consider reading the following papers: [Souza2002], [Nunes2001] and M. Veithen PhD thesis. Finally, the extension to the PAW formalism specifically in ABINIT is discussed in [Gonze2009] and [Zwanziger2012].

This tutorial should take about 1 hour and 30 minutes.

Note

Supposing you made your own installation of ABINIT, the input files to run the examples are in the ~abinit/tests/ directory where ~abinit is the absolute path of the abinit top-level directory. If you have NOT made your own install, ask your system administrator where to find the package, especially the executable and test files.

In case you work on your own PC or workstation, to make things easier, we suggest you define some handy environment variables by executing the following lines in the terminal:

export ABI_HOME=Replace_with_absolute_path_to_abinit_top_level_dir # Change this line
export PATH=$ABI_HOME/src/98_main/:$PATH      # Do not change this line: path to executable
export ABI_TESTS=$ABI_HOME/tests/             # Do not change this line: path to tests dir
export ABI_PSPDIR=$ABI_TESTS/Psps_for_tests/  # Do not change this line: path to pseudos dir

Examples in this tutorial use these shell variables: copy and paste the code snippets into the terminal (remember to set ABI_HOME first!) or, alternatively, source the set_abienv.sh script located in the ~abinit directory:

source ~abinit/set_abienv.sh

The ‘export PATH’ line adds the directory containing the executables to your PATH so that you can invoke the code by simply typing abinit in the terminal instead of providing the absolute path.

To execute the tutorials, create a working directory (Work*) and copy there the input files of the lesson.

Most of the tutorials do not rely on parallelism (except specific tutorials on parallelism). However you can run most of the tutorial examples in parallel with MPI, see the topic on parallelism.

1 Ground-state properties of AlP and general parameters

Before beginning, you might consider working in a different subdirectory, as for the other tutorials. For example, create Work_polarization in $ABI_TESTS/tutorespfn/Input

In this tutorial we will assume that the ground-state properties of AlP have been previously obtained, and that the corresponding convergence studies have been done. We will adopt the following set of generic parameters:

acell   3*7.2728565836E+00
ecut    5    
ecutsm  0.5
dilatmx 1.05
nband   4 (=number of occupied bands)
ngkpt   6 6 6
nshiftk 4
shiftk  0.5 0.5 0.5
        0.5 0.0 0.0
        0.0 0.5 0.0
        0.0 0.0 0.5

pseudopotentials  Pseudodojo_nc_sr_04_pw_standard_psp8/P.psp8
                  Pseudodojo_nc_sr_04_pw_standard_psp8/Al.psp8

In principle, the acell to be used should be the one corresponding to the optimized structure at the ecut, and ngkpt combined with nshiftk and shiftk, chosen for the calculations.

For the purpose of this tutorial, in order to limit the duration of the runs, we are working at a low cutoff of 5 Ha, for which the optimized lattice constant is equal to $7.27\times 2/\sqrt{2}=10.29~\mathrm{Bohr}$. Nonetheless this value is close to that obtained with a highly converged geometry optimization, of 10.25~Bohr. As always, if you adapt this tutorial to your own research, it is critical to perform full convergence studies. Before going further, you might refresh your memory concerning the other variables: ecutsm, dilatmx, ngkpt, nshiftk, and shiftk.

Note as well that the pseudopotentials used here are freely available from Pseudo Dojo. The ones chosen here for P and Al use the Perdew-Wang parameterization of the local density approximation (LDA); this is done to facilitate comparison of the results of this tutorial with those of Non-linear properties.

2 Berry phase calculation of polarization in zero field

In this section, you will learn how to perform a Berry phase calculation of the polarization. As a practical problem we will try to compute the Born effective charges from finite difference of the polarization (under finite atomic displacements), for AlP.

You can now copy the file tpolarization_1.abi to Work_polarization,

cd $ABI_TESTS/tutorespfn/Input
mkdir Workpolarization_
cd Workpolarization_
cp ../tpolarization_1.abi .

View tests/tutorespfn/Input/tpolarization_1.abi

Note that two pseudopotentials are mentioned in this input file: one for the phosphorus atom, and one for the aluminum atom. The first listed, for P in this case, will define the first type of atom. The second listed, for Al, will define the second type of atom. This might be the first time that you encounter this situation (more than one type of atom) in the tutorials, in contrast with the four “basic” tutorials. Because of the use of more than one type of atom, the following input variables must be present:

• ntypat
• typat

You can start the calculation. It should take about 90 seconds on a typical desktop machine. In the meantime, examine the tpolarization_1.abi file. It includes three computations (see the section labelled as atomic positions) corresponding to, first, the reference optimized structure ($\tau=0$), and then to the structure with the Al atom displaced from 0.01 bohr to the right and to the left (referred to as $\tau = +0.01$ and $\tau =-0.01$). These are typical for the amplitude of atomic displacement in this kind of finite difference computation. Notice also that the displacements are given using xcart, that is, explicitly in Cartesian directions in atomic units, rather than the primitive cell axes (which would use xred). This makes the correspondence with the polarization output in Cartesian directions much simpler to understand.

There are two implementations of the Berry phase within ABINIT. One is triggered by positive values of berryopt and was implemented by Na Sai. The other one is triggered by negative values of berryopt and was implemented by Marek Veithen. Both are suitable to compute the polarization, however, here we will focus on the implementation of Marek Veithen for two reasons. First, the results are directly provided in Cartesian coordinates at the end of the run (while the implementation of Na Sai reports them in reduced coordinates). Second, the implementation of Marek Veithen is the one to be used for the finite electric field calculation as described in the next section. Finally, note also that Veithen’s implementation works with kptopt = 1 or 2 while Na Sai implementation is restricted to kptopt = 2, which is less convenient.

The input file is typical for a self-consistent ground state calculation. In addition to the usual variables, for the Berry phase calculation we simply need to include berryopt (see also rfdir, the default being usually adequate):

berryopt      -1

Make the run, then open the output file and look for the occurrence “Berry”. The output reports values of the Berry phase for individual k-point strings.

 Computing the polarization (Berry phase) for reciprocal vector:
  0.16667  0.00000  0.00000 (in reduced coordinates)
 -0.01620  0.01620  0.01620 (in cartesian coordinates - atomic units)
 Number of strings:   144
 Number of k points in string:    6

 Summary of the results
 Electronic Berry phase     2.206976733E-03
            Ionic phase    -7.500000000E-01
            Total phase    -7.477930233E-01
    Remapping in [-1,1]    -7.477930233E-01

           Polarization    -1.632453164E-02 (a.u. of charge)/bohr^2
           Polarization    -9.340041842E-01 C/m^2

The “Remapping in [-1,1]” is there to avoid the quantum of polarization. As discussed in [Djani2012], the indeterminacy of the quantum phase, directly related to the quantum of polarization, can lead to spurious effects (see Fig. 2 of the above-mentioned paper). By remapping on the [-1,1] interval, any indeterminacy is removed. However, removing such a quantum of polarization between two calculations might give the false impression that one is on the same polarization branch in the two calculations, while actually the branch is made different by this remapping. Cross-checking the polarization results by computing the Born effective charge, further multiplied by the displacements between the two geometries is an excellent way to estimate the amplitude of the polarization.

Other subtleties of Berry phases, explained in [Vanderbilt1993], also apply. First, note that neither the electronic Berry phase nor the ionic phase vanish in this highly symmetric case, contrary to intuition. Even though AlP does not have inversion symmetry, it does have tetrahedral symmetry, which would be enough to make an ordinary vector vanish. But a lattice-valued vector does not have to vanish: the lattice just has to transform into itself under the tetrahedral point group. The ionic phase corresponds actually to a lattice-valued vector (-¾ -¾ -¾). Concerning the electronic phase, it does not exactly vanish, unless the sampling of k points becomes continuous.

If you go further in the file you will find the final results in cartesian coordinates. You can collect them for the different values of $\tau$.

$\tau = 0$

 Polarization in cartesian coordinates (a.u.):
     Total: -0.282749182E-01  -0.282749182E-01  -0.282749182E-01

 Polarization in cartesian coordinates (C/m^2):
     Total: -0.161774270E+01  -0.161774270E+01  -0.161774270E+01

$\tau = +0.01$

 Polarization in cartesian coordinates (a.u.):
     Total: -0.281920467E-01  -0.282749119E-01  -0.282749119E-01

 Polarization in cartesian coordinates (C/m^2):
     Total: -0.161300123E+01  -0.161774234E+01  -0.161774234E+01

$\tau = -0.01$

 Polarization in cartesian coordinates (a.u.):
     Total: -0.283577762E-01  -0.282749119E-01  -0.282749119E-01

 Polarization in cartesian coordinates (C/m^2):
     Total: -0.162248340E+01  -0.161774234E+01  -0.161774234E+01

From the previous data, we can extract the Born effective charge of Al. Values to be used are those in a.u., in order to find the charge in electron units. It corresponds to (the volume of the primitive unit cell must be specified in atomic units too): $$ Z^* = \Omega_0 \frac{P(\tau = +0.01) - P(\tau = -0.01)}{2\tau} $$ $$= 272.02 \frac{ (-2.8192\times 10^{-2}) - (-2.8358\times 10^{-2})}{0.02} $$ $$ = 2.258$$

For comparison, the same calculation using Density-Functional Perturbation Theory (DFPT) can be done by using the file $ABI_TESTS/tutorespfn/Input/tpolarization_2.abi.

View tests/tutorespfn/Input/tpolarization_2.abi

Actually, the file tpolarization_2.abi not only leads to the computation of the Born effective charges, but also the computation of the piezoelectric constants (see later). You can review how to use DFPT in the tutorial Response-function 1 and tutorial Response-function 2 tutorials.

Note

An interesting feature of tpolarization_2.abi is the use of berryopt2 -2 in the second data set. This input variable causes the computation of the DDK wavefunctions using a finite difference formula, rather than the DFPT approach triggered by rfddk. Although not strictly required in the present DFPT calculation, the finite difference approach is necessary in the various Berry’s phase computations of polarization, in order to maintain phase coherency between wavefunctions at neighboring k points. Therefore in the present tutorial we use the finite difference approach, in order to compare the results of the Berry’s phase computation to those of DFPT more accurately.

Warning

The use of kpoint overlaps in Berry’s phase calculations is necessary, but causes the results to converge much more slowly with kpoint mesh density than other types of calculations. It is critical in production work using Berry’s phase methods to check carefully the convergence with respect to kpoint mesh density.

Go ahead and run the input file, and have a look at the output file, to identify the place where the Born effective charge is written (search for the phrase “Effective charges”). The value we get from DFPT is 2.254, in surprisingly good agreement with the above-mentioned value of 2.258. This level of agreement is fortuitous for unconverged calculations. Both methods (finite-difference and DFPT) will tend to the same value for better converged calculations.

The DDB file generated by $ABI_TESTS/tutorespfn/Input/tpolarization_2.abi can be used as input to anaddb for further processing, using the input file tpolarization_3.abi and the tpolarization_3.files file.

View tests/tutorespfn/Input/tpolarization_3.files View tests/tutorespfn/Input/tpolarization_3.abi

Note

While the abinit program itself takes its input file as an argument, the anaddb post-processing program depends in general on multiple input files, and therefore it is more convenient to pipe in a file whose contents are just the names of the files that anaddb should ultimately use. In the present case, the piped-in file tpolarization_3.files is written such that the DDB file is named tpolarization_2o_DS3_DDB (this is defined in the third line of tpolarization_3.files). In the event of a mismatch, you can either edit tpolarization_3.files to match the DDB you have, or change the name of the DDB file.

The DFPT calculation yields the following piezoelectric constants, as found in tpolarization_3.abo:

 Proper piezoelectric constants (clamped ion) (unit:c/m^2)

      0.00000000     -0.00000000      0.00000000
      0.00000000      0.00000000      0.00000000
     -0.00000000     -0.00000000     -0.00000000
     -0.64263948      0.00000000      0.00000000
      0.00000000     -0.64263948      0.00000000
      0.00000000      0.00000000     -0.64263948
 ....
 Proper piezoelectric constants (relaxed ion) (unit:c/m^2)

      0.00000000      0.00000000     -0.00000000
      0.00000000     -0.00000000     -0.00000000
      0.00000000     -0.00000000     -0.00000000
      0.13114427      0.00000000     -0.00000000
      0.00000000      0.13114427     -0.00000000
     -0.00000000     -0.00000000      0.13114427

View tests/tutorespfn/Refs/tpolarization_3.abo

The piezoelectric constants here are the change in polarization as a function of strain [Wu2005]. The rows are the strain directions using Voigt notation (directions 1-6) while the columns are the polarization directions. In the $\bar{4}3m$ crystal class of AlP, the only non-zero piezoelectric elements are those associated with shear strain (Voigt notation strains $e_4$, $e_5$, and $e_6$) [Nye1985].

The relaxed ion values, where the ionic relaxation largely suppresses the electronic piezoelectricity, will be more difficult to converge than the clamped ion result.

Because the Berry phase approach computes polarization, it can also be used to compute the piezoelectric constants from finite difference of polarization with respect to strains. This can be done considering clamped ions or relaxed ions configurations. For this purpose, have a look at the files t_polarization4.abi (clamped ions) and t_polarization5.abi (relaxed ions).

View tests/tutorespfn/Input/tpolarization_4.abi View tests/tutorespfn/Input/tpolarization_5.abi

In these input files the finite strain is applied by multiplying the $e_4$ (Voigt notation) strain tensor by the (dimensionless) unit cell vectors: $$ \left[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & e_4/2 \\ 0 & e_4/2 & 1 \\ \end{matrix}\right] \left[\begin{matrix} 0 & 1/\sqrt{2} & 1/\sqrt{2} \\ 1/\sqrt{2} & 0 & 1/\sqrt{2} \\ 1/\sqrt{2} & 1/\sqrt{2} & 0 \\ \end{matrix}\right] = \left[\begin{matrix} 0 & 1/\sqrt{2} & 1/\sqrt{2} \\ (1+e_4/2)/\sqrt{2} & e_4/2\sqrt{2} & 1/\sqrt{2} \\ (1+e_4/2)/\sqrt{2} & 1/\sqrt{2} & e_4/2\sqrt{2} \\ \end{matrix}\right] $$ Don’t forget that in the input file, vectors are read in as rows of numbers, not columns!

Notice how in the relaxed ion case, the input file includes ionmov = 2 and optcell = 0, in order to relax the ion positions at fixed cell geometry. These calculations should give the following final results (obtained by taking finite difference expressions of the strains for different electric fields): $-0.6427~C/m^2$ for the clamped ion case, and $0.1310~C/m^2$ for the relaxed ion case.

For example, the clamped ion piezoelectric constant was obtained from tpolarization_4.abo:

== DATASET  2 ==========================================================
....
 Polarization in cartesian coordinates (C/m^2):
     Total: -0.162420887E+01  -0.162587046E+01  -0.162587046E+01
....    
== DATASET  3 ==========================================================
     ...
 Polarization in cartesian coordinates (C/m^2):
     Total: -0.161135421E+01  -0.160969264E+01  -0.160969264E+01

The difference between -0.162420887E+01 (obtained at strain +0.01) and -0.161135421E+01 (obtained at train -0.01) gives the finite difference -0.0128546, which, divided by 0.02 (the total change in strain) gives -0.6427, as noted above.

3 Finite electric field calculations

In this section, you will learn how to perform a calculation with a finite electric field.

You can now copy the file $ABI_TESTS/tutorespfn/Input/tpolarization_6.abi to Work_polarization.

View tests/tutorespfn/Input/tpolarization_6.abi

You can start the run immediately. It performs a finite field calculation at clamped atomic positions. You can look at this input file to identify the features specific to the finite field calculation.

As general parameters, one has to specify nband, nbdbuf and kptopt:

        nband          4
        nbdbuf         0
        kptopt         1

As a first step (dataset 11), the code must perform a Berry phase calculation in zero electric field. For that purpose, it is necessary to set the values of berryopt:

        berryopt11     -1

Warning

You cannot use berryopt to +1 to initiate a finite field calculation. You must begin with berryopt -1.

After that, there are different steps corresponding to various values of the electric field, as set by efield. For those steps, it is important to take care of the following parameters, as shown here for example for dataset 21:

        berryopt21     4
        efield21       0.0001  0.0001  0.0001
        getwfk21       11

The electric field is applied here along the [111] direction. It must be incremented step by step (it is not possible to go to high field directly). At each step, the wavefunctions of the previous step must be used. When the field gets large, it is important to check that it does not significantly exceed the critical field for Zener breakthrough (the drop of potential over the Born-von Karmann supercell must be smaller than the gap). In practice, the number of k-point must be enlarged to reach convergence. However, at the same time, the critical field becomes smaller. In practice, reasonable fields can still be reached for k-point grids providing a reasonable degree of convergence. A compromise must however be found.

As these calculations are quite long, the input file has been limited to a small number of small fields. Three cases have been selected: $E = 0$, $E = +0.0001$ and $E = -0.0001$. If you have time later, you can perform more exhaustive calculations over a larger set of fields.

Various quantities can be extracted from the finite field calculation at clamped ions using finite difference techniques: the Born effective charge $Z^*$ can be extracted from the difference in forces at different electric fields, the optical dielectric constant can be deduced from the polarizations at different fields, and the clamped ion piezoelectric tensor can be deduced from the stress tensor at different fields. As an illustration we will focus here on the computation of $Z^*$.

Examine the output file. For each field, the file contains various quantities that can be collected. For the present purpose, we can look at the evolution of the forces with the field and extract the following results from the output file:

$E=0$

cartesian forces (hartree/bohr) at end:
   1     -0.00000000000000    -0.00000000000000    -0.00000000000000
   2     -0.00000000000000    -0.00000000000000    -0.00000000000000

$E = +0.0001$

 cartesian forces (hartree/bohr) at end:
    1     -0.00022532204220    -0.00022532204220    -0.00022532204220
    2      0.00022532204220     0.00022532204220     0.00022532204220

$E = -0.0001$

 cartesian forces (hartree/bohr) at end:
    1      0.00022548273033     0.00022548273033     0.00022548273033
    2     -0.00022548273033    -0.00022548273033    -0.00022548273033

In a finite electric field, the force on atom $A$ in direction $i$ can be written as: $$ F_{A,i} = Z^*_{A,ii}E + \Omega_0 \frac{d\chi}{d\tau} E^2 $$

The value for positive and negative fields above are nearly the same, showing that the quadratic term is almost negligible. This clearly appears in the figure below where the field dependence of the force for a larger range of electric fields is plotted.

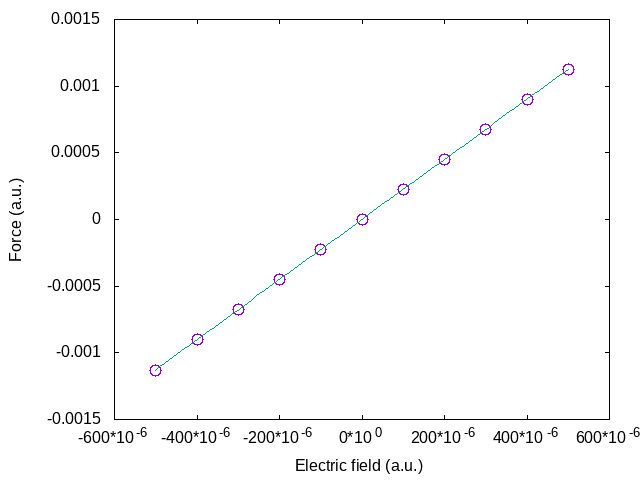
We can therefore extract with good accuracy the Born effective charge as:

$$Z^*_{\mathrm Al} = \frac{F_{\mathrm Al}(E=+0.0001) - F_{\mathrm Al}(E=-0.0001)}{2\times 0.0001} = \frac{(2.2532\times 10^{-4}) - (-2.2548\times 10^{-4})}{0.0002} = 2.254.$$

This value is similar to the value reported from DFPT. If you do calculations for more electric fields, fitting them with the general expression of the force above (including the $E^2$ term), you can find the $d\chi/d\tau$ term. From the given input file tpolarization_6.abi, using all the fields, you should find $d\chi/d\tau$ for Al of = -0.0295.

Going back to the output file, you can also look at the evolution of the polarization with the field.

$E = 0$

 Polarization in cartesian coordinates (a.u.):
     Total: -0.282749182E-01  -0.282749182E-01  -0.282749182E-01

$E = +0.0001$

 Polarization in cartesian coordinates (a.u.):
     Total: -0.282310128E-01  -0.282310128E-01  -0.282310128E-01

$E = -0.0001$

 Polarization in cartesian coordinates (a.u.):
     Total: -0.283187730E-01  -0.283187730E-01  -0.283187730E-01

In a finite electric field, the polarization in terms of the linear and quadratic susceptibilities is, in SI units,

$$P_i = \epsilon_0\chi^{(1)}_{ij} E_j + \epsilon_0\chi^{(2)}_{ijk} E_jE_k$$

or, in atomic units:

$$P_i = \frac{1}{4\pi}\chi^{(1)}_{ij} E_j + \frac{1}{4\pi}\chi^{(2)}_{ijk} E_jE_k,$$

as $4\pi\epsilon_0 = 1$ in atomic units.

The change of polarization for positive and negative fields above are nearly the same, showing again that the quadratic term is almost negligible. This clearly appears in the figure below where the field dependence of the polarization for a larger range of electric fields is plotted.

We can therefore extract the linear optical dielectric susceptibility:

$$\chi_{11}^{(1)} = 4\pi\frac{P_1(E=+0.0001) - P_1(E=-0.0001)}{2\times 0.0001} = 4\pi\frac{(-2.82310\times 10^{-2}) - (-2.83188\times 10^{-2})}{0.0002} = 5.5166.$$

The relative permittivity, also known as the dielectric constant, is

$$\epsilon_{11}/\epsilon_0 = 1+ \chi^{(1)}_{11} = 6.5166.$$

This value is a bit over the value of 6.463 obtained by DFPT from tpolarization_3.abi. Typically, finite field calculations converge with the density of the k point grid more slowly than DFPT calculations.

If you do calculations for more electric fields, fitting them with the general expression of the polarization above (including the $E^2$ term) you can find the non- linear optical susceptibility $\chi^{(2)}/4\pi$ (in atomic units). For tpolarization_6.abi you should find $\chi^{(2)}/4\pi = 2.5427$, so in SI units $\chi^{(2)} = 62.14~\mathrm{pm/V}$ and $d_{36} = 15.54~\mathrm{pm/V}$. The relationship between the $\chi^{(2)}_{ijk}$ tensor and the $d_{ij}$ tensor (the quantity reported by abinit in a nonlinear optics DFPT computation) involves a variety of symmetries and is explained in detail in the book [Boyd2020].

Looking at the evolution of the stress with electric field (see graphic below), you should also be able to extract the piezoelectric constants. You can try to do it as an exercise. As the calculation here was at clamped ions, you will get the clamped ion proper piezoelectric constants. You should obtain -0.6365 C/m$^2$. The relationships between the various response functions under conditions of strain, stress, field, and so forth are discussed in depth in [Wu2005].

You can modify the previous input file to perform a finite field calculation combined with ion relaxation, similarly to how tpolarization_5.abi was modified from tpolarization_4.abi, giving access to the the relaxed ion proper piezoelectric constant. From the output of this run, analyzing the results in the same way as before, you should obtain 0.1311 C/m$^2$ for the relaxed ion piezoelectric constant.