fold2bloch analysis tool¶
Unfolding the electronic structure of a lattice of Hydrogen atoms.¶
Supercells are often used in electronic structure calculations in order to model compound alloys, defects, etc. The band structure obtained directly from these calculations is hard to interpret due to the Brillouin zone folding as a result of its reduced size for the supercell, compared to that for the unperturbed host unit cell. The unfolding technique used in Abinit is the one presented in [Rubel2014].
This tutorial aims at demonstrating how to unfold the band structure of a supercell and present it in the basis of conventional Bloch wave vectors inherent to the unperturbed unit cell. We will construct a supercell of 6 hydrogen atoms, perform self-consistent cycle and plot the corresponding band structure. At the end, we will recover the familiar dispersion relation using the fold2Bloch utility. See also the fold2bloch help file.
This tutorial should take about 1 hour.
Note
Supposing you made your own installation of ABINIT, the input files to run the examples are in the ~abinit/tests/ directory where ~abinit is the absolute path of the abinit top-level directory. If you have NOT made your own install, ask your system administrator where to find the package, especially the executable and test files.
In case you work on your own PC or workstation, to make things easier, we suggest you define some handy environment variables by executing the following lines in the terminal:
export ABI_HOME=Replace_with_absolute_path_to_abinit_top_level_dir # Change this line
export PATH=$ABI_HOME/src/98_main/:$PATH # Do not change this line: path to executable
export ABI_TESTS=$ABI_HOME/tests/ # Do not change this line: path to tests dir
export ABI_PSPDIR=$ABI_TESTS/Pspdir/ # Do not change this line: path to pseudos dir
Examples in this tutorial use these shell variables: copy and paste
the code snippets into the terminal (remember to set ABI_HOME first!) or, alternatively,
source the set_abienv.sh script located in the ~abinit directory:
source ~abinit/set_abienv.sh
The ‘export PATH’ line adds the directory containing the executables to your PATH so that you can invoke the code by simply typing abinit in the terminal instead of providing the absolute path.
To execute the tutorials, create a working directory (Work*) and
copy there the input files of the lesson.
Most of the tutorials do not rely on parallelism (except specific tutorials on parallelism). However you can run most of the tutorial examples in parallel with MPI, see the topic on parallelism.
Creating a Hydrogen supercell structure¶
Let’s begin with the simplest structure: a lattice of hydrogen atoms. It is a convenient starting point since the hybridization between \(s\)-orbitals results in a well known dispersion relation for the energy eigenvalues as a function of the wave vector \(k\):
Here \(b\) is the lattice spacing and \(A\) reflects the strength of hybridization between adjacent \(s\)-orbitals. For more details please refer to the Feynman’s Lectures on Physics (vol 3, chapter 13).
Our model structure will be a cubic lattice of hydrogen atoms spaced 3 Bohr apart. The primitive cell contains only one atom. Here we chose to represent the same structure with a 6 atom supercell. Such a large cell is redundant in this case, since there is nothing that disturbs the original symmetry. However, we made this choice on purpose in order to observe the zone folding.
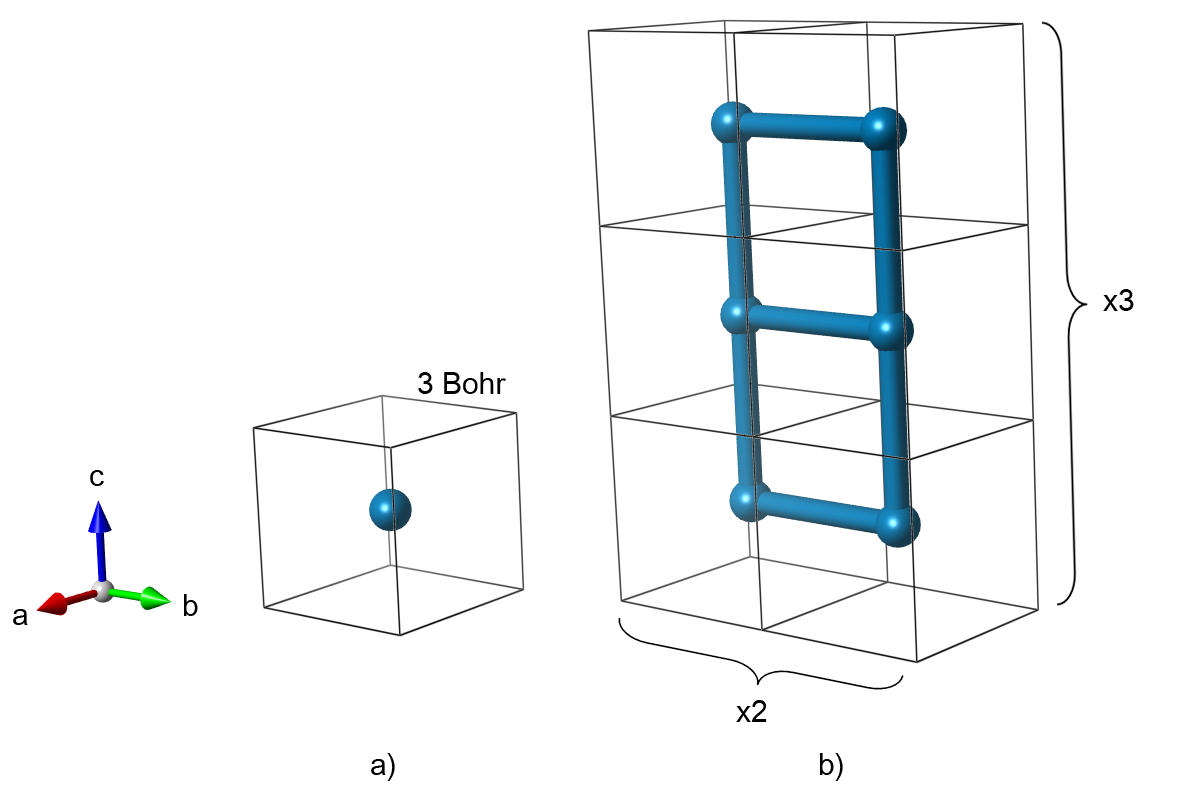
- Fig. 1: Primitive unit cell (a) and 1x2x3 supercell (b) that represent a cubic lattice of hydrogen atoms.
Since we are interested in the band structure, we need to select a path in the reciprocal space which will be used for plotting. The supercell was expanded in Y and Z directions. Accordingly, the reciprocal space shrinks along the same directions. We select those directions for the band structure plot as they will be affected by the zone folding.

- Fig. 2: Brillouin zone of the supercell.
Before beginning, you might consider to work in a different subdirectory as for the other tutorials. Why not Work_fold2Bloch?
In order to use the fold2Bloch, you need to first generate a wave function file (WFK file).
For this purpose, copy the file tests/tutorial/Input/tfold2bloch_1.abi in the directory ~abinit/tests/tutorial/Input/Work_fold2Bloch.
cd $ABI_TESTS/tutorial/Input
mkdir Work_fold2Bloch
cd Work_fold2Bloch
cp ../tfold2bloch_1.abi .
# H6 Supercell # Generates a 6 atom Hydrogen supercell with the multiplicity of 1:2:3 (x:y:z), and computes the band structure. ndtset 2 # There will be two datasets here: SCF run and the band structure #Dataset 2 : the band structure iscf2 -2 getden2 -1 # get charge density from the 1st run kptopt2 -5 # band structure plot with 5 intervals ndivk2 10 10 1 10 10 # number of divisors for each interval kptbounds2 0.0 -0.5 0.0 # Y point 0.0 0.0 0.0 # Gamma point 0.0 0.5 0.0 # Y point 0.0 0.0 -0.5 # Z point 0.0 0.0 0.0 # Gamma 0.0 0.0 0.5 # Z point tolwfr2 1.0d-12 enunit2 1 # Will output the eigenenergies in eV ####################################################################### #Common input variables #Definition of the unit cell acell 3.0 6.0 9.0 # [Bohr] rprim 1 0 0 0 1 0 0 0 1 chkprim 0 # Do not check for primitive cell, as we are specifically using a supercell in this tutorial. #Definition of the atom types and pseudopotentials ntypat 1 znucl 1 pp_dirpath "$ABI_PSPDIR" pseudos "Psdj_paw_pw_std/H.xml" #Definition of the atoms natom 6 typat 1 1 1 1 1 1 xred 0.0 0.0 0.0 0.0 0.0 1/3 0.0 0.0 2/3 0.0 0.5 0.0 0.0 0.5 1/3 0.0 0.5 2/3 #Numerical parameters of the calculation : planewave basis set and k point grid ecut 20.0 # Maximum kinetic energy cutoff (Hartree) pawecutdg 40 # PAW - Energy CUToff for the Double Grid ngkpt 3 2 1 # 3x2x1 Monkhorst-Pack grid nshiftk 1 # Use one copy of grid only (default) shiftk 0.0 0.0 0.0 # Unshifted K-mesh #Parameters for the SCF procedure diemac 9.0 # Model dielectric preconditioner nstep 100 # Maximum number of SCF iterations tolvrs 1.0d-6 # tolerance for potential residual ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% test_chain = tfold2bloch_1.abi, tfold2bloch_2.abi #%% [files] #%% files_to_test = #%% tfold2bloch_1.abo, tolnlines=38, tolabs=2.0e-4, tolrel=2.0e-02 #%% [paral_info] #%% max_nprocs = 2 #%% [extra_info] #%% authors = O. Rubel #%% keywords = FOLD2BLOCH, PAW #%% description = #%% H6 Supercell #%% Generates a 6 atom Hydrogen supercell with the multiplicity of 1:2:3 (x:y:z) #%% Produces a WFK file to be analyzed with fold2bloch #%%<END TEST_INFO>
The input file has two datasets, the first to generate the WFK file, and the second to draw the band structure. Now you are ready to run Abinit. Issue the following:
abinit tfold2bloch_1.abi > tfold1bloch_1.log &
This will generate a self consistent charge density for the 6 Hydrogen atom supercell structure, and the wave function file, tfold2bloch_1o_DS1_WFK, which is needed for unfolding with fold2Bloch.
Folded band structure¶
Before we proceed with the unfolding, let’s plot the “standard” band structure of a supercell. We will be looking for signatures of the zone folding. In order to do this, there are several possibilities. You might e.g. rely on Abipy (see below), or on Matlab. This tutorial was initally illustrated using Matlab, for which you will need the following scripts
- energy_eig-abinit.sh
- plot_band.m
that are located at $ABI_HOME/doc/tutorial/fold2Bloch_assets/ . Copy them to your work directory.
Execute the energy_eig-abinit.sh script
./energy_eig-abinit.sh tfold2bloch_1o_DS2_EIG
This will generate an output file: tfold2bloch_1o_DS2_EIG.dat
Edit plot_band.m file and point to the newly created tfold2bloch_1o_DS2_EIG.dat file.
data=load('tfold2bloch_1o_DS2_EIG.dat');
Then, run the plot_band.m script in MatLab
plot_band.m
This will plot the band structure of the 6 atom Hydrogen supercell created.
Lastly, compare the image obtained to the band structure image below.
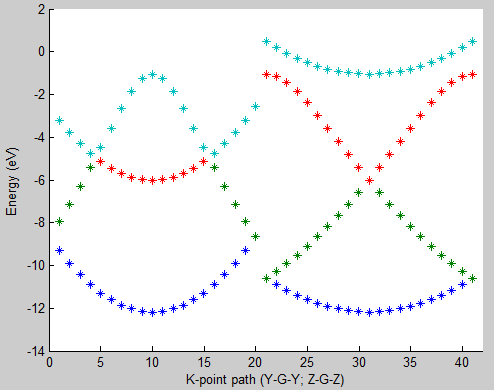
- Fig. 3: 6 atom hydrogen supercell band structure plot
Here you can see that the band structure does not look like a cosine function along directions Y-Gamma and Z-Gamma. The band structure is folded according to the multiplicity along those directions used when constructing the supercell (Fig. 1b).
Tip
If AbiPy is installed on your machine, you can use the abiopen.py script
with the --expose option to visualize the band dispersion:
abiopen.py tfold2bloch_1o_DS2_GSR.nc --expose
Bloch spectral weights with fold2Bloch¶
Next step is to execute fold2Bloch using the wave function file from the 2nd dataset, and multiplicity in the corresponding directions, used when constructing the super-cell (x:y:z), included as part of the command line arguments. For this example the multiplicity used was (1:2:3)
Execute the following command:
fold2Bloch tfold2bloch_1o_DS2_WFK 1:2:3
You should see the following:
***********************
** Fold2Bloch V 1.1 **
**Build Mar 16, 2015**
***********************
Reading eigenvalues from: tfold2bloch_1o_DS2_WFK , with iomode: IO_MODE_MPI
wfk_read_eigenvalues completed. cpu: 0.03 [s] , wall: 0.04 [s] <<< TIME
- Creating netcdf file WITHOUT MPI-IO support: tfold2bloch_FOLD2BLOCH.nc
2% Processing K point: 0.000000 -0.500000 0.000000
4% Processing K point: 0.000000 -0.450000 0.000000
7% Processing K point: 0.000000 -0.400000 0.000000
...
95% Processing K point: 0.000000 0.000000 0.400000
97% Processing K point: 0.000000 0.000000 0.450000
100% Processing K point: 0.000000 0.000000 0.500000
Number of K points processed: 42
Data was written to: tfold2bloch.f2b
Data format: KX, KY, KZ, Eigenvalue(Ha), Weight
That output tells us which K-point was processed, total number of K-points processed, output file, and the format that the data is written in.
Now take a look at the tfold2Bloch.f2b. The first few lines should be as follows:
0.000000 -0.250000 0.000000 -0.308342 0.589037
0.000000 -0.250000 0.333333 -0.308342 0.000000
0.000000 -0.250000 -0.333333 -0.308342 0.000000
0.000000 0.250000 0.000000 -0.308342 0.410963
0.000000 0.250000 0.333333 -0.308342 0.000000
0.000000 0.250000 -0.333333 -0.308342 0.000000
0.000000 -0.250000 0.000000 -0.308342 0.410963
0.000000 -0.250000 0.333333 -0.308342 0.000000
0.000000 -0.250000 -0.333333 -0.308342 0.000000
0.000000 0.250000 0.000000 -0.308342 0.589037
0.000000 0.250000 0.333333 -0.308342 0.000000
0.000000 0.250000 -0.333333 -0.308342 0.000000
0.000000 -0.250000 0.000000 -0.083709 0.000000
0.000000 -0.250000 0.333333 -0.083709 0.593925
0.000000 -0.250000 -0.333333 -0.083709 0.025041
0.000000 0.250000 0.000000 -0.083709 0.000000
0.000000 0.250000 0.333333 -0.083709 0.133575
0.000000 0.250000 -0.333333 -0.083709 0.247460
0.000000 -0.250000 0.000000 -0.083709 0.000000
0.000000 -0.250000 0.333333 -0.083709 0.193298
0.000000 -0.250000 -0.333333 -0.083709 0.218686
0.000000 0.250000 0.000000 -0.083709 0.000000
0.000000 0.250000 0.333333 -0.083709 0.564322
0.000000 0.250000 -0.333333 -0.083709 0.023694
0.000000 -0.225000 0.000000 -0.332652 1.000000
0.000000 -0.225000 0.333333 -0.332652 0.000000
...
Let’s take a moment to analyse the output. Columns 1-3 correspond to kx, ky and kz of the unfolded bands; the 4th column is the energy eigenvalue in [Ha] and the 5th column corresponds to a spectral weight of the k-point after unfolding. Do not confuse it with k-point weight, which represents its multiplicity in the Brillouin zone. Since our supercell contains 6 unit cells (1 x 2 x 3), each eigenvalue in the solution contains information about 6 Bloch wave vectors, i.e., unfolded into 6 k-points. The relative contribution of these k-points is determined by the spectral weight.
Lines 1-6 represent unfolding of the 1st eigenvalue of -0.31796 Ha. This eigenvalue corresponds to the Bloch wave vectors of (0 ±½ 0) as they have a non-zero weight. The weights total 1 for normalization. This eigenvalue is degenerate, so lines 7-12 look very similar. When a disorder is present (in a form of defects, distortions, impurities) individual eigenstates may not express an exclusive Bloch character any longer. This can have some interesting consequences for transport or optical properties, which are not apparent from the folded band structure.
Note
the whole output is much bigger than the sample provided above. For the band structure visualization proceed to the next step.
Unfolded band structure¶
Lets visualize the unfolded band structure. It is different from a regular band structure plot, though. Now we have one additional dimension – the Bloch spectral weight. There are several alternative visualization strategies. Here we use the scatter plot with the point size proportional to the spectral weight. The following MatLab script will help you build a graph for any fold2Bloch output: ubs_dots.m
Make sure the following parameters in ubs_dots.m are set as follows:
KPATH = [0 1/2 0; ...
0 0 0; ...
0 0 1/2];
finpt='tfold2bloch_1o.f2b';
and:
G = [0.3333333 0.0000000 0.0000000;
0.000000 0.1666667 0.0000000;
0.000000 0.000000 0.1111111]; % Reciprocal latt. vect. [Bohr^-1] from *.out
Reciprocal lattice vector information must match that in tfold2bloch_1.abo:
Real(R)+Recip(G) space primitive vectors, cartesian coordinates (Bohr,Bohr^-1):
R(1)= 3.0000000 0.0000000 0.0000000 G(1)= 0.3333333 0.0000000 0.0000000
R(2)= 0.0000000 6.0000000 0.0000000 G(2)= 0.0000000 0.1666667 0.0000000
R(3)= 0.0000000 0.0000000 9.0000000 G(3)= 0.0000000 0.0000000 0.1111111
Unit cell volume ucvol= 1.6200000E+02 bohr^3
Angles (23,13,12)= 9.00000000E+01 9.00000000E+01 9.00000000E+01 degrees
For graphing any other fold2Bloch output, make sure that the “%%Init Parameters” are set accordingly to size of the supercell constructed.
After running the script you should see the following graph:
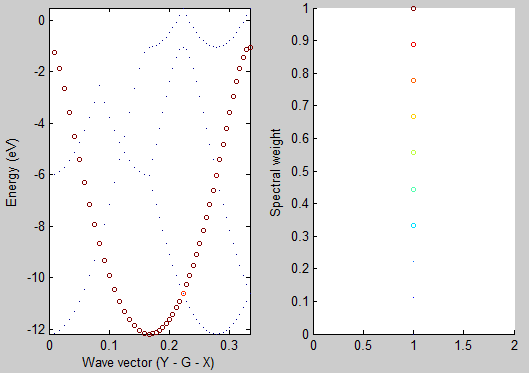
As you can see the unfolded band structure perfectly reproduces the anticipated dispersion relation \(E(k)=E_0 - 2A \cos(kb)\). We can even estimate the magnitude of the hopping matrix element between adjacent atoms \(V_{ssG} = -A\). The band width is \(4A = (-1) - (-12) = 11\) eV which results in \(V_{ssG} = -2.75\) eV.
To analyze the results with AbiPy use:
abiopen.py tfold2bloch_FOLD2BLOCH.nc
to open the file inside ipython and then type, at the request of ipython:
# Plot unfolded bands along the path defined by kbounds.
# 'In [x]' are ipython prompts, do no type them, type only 'kbounds ...' then 'klabels ...' then 'abifile...'
In [1] kbounds = [0, 1/2, 0, 0, 0, 0, 0, 0, 1/2]
In [2] klabels = ["Y", r"$\Gamma$", "X"]
In [3] abifile.plot_unfolded(kbounds, klabels, title="Unfolded bands")
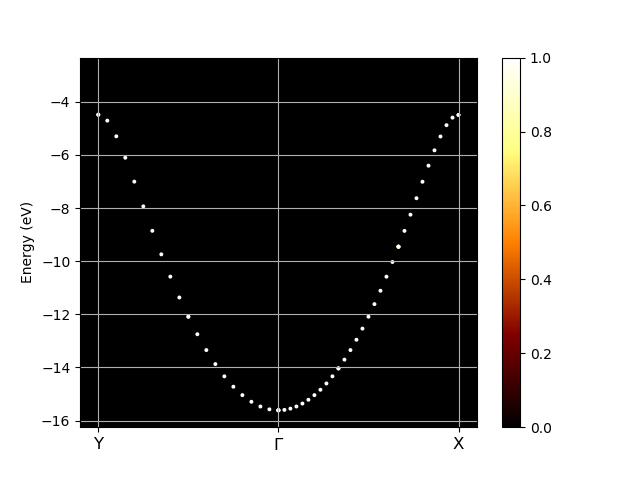
See also this example.