Electron-phonon tutorial¶

Electron-Phonon interaction and superconducting properties of Al.¶

This tutorial demonstrates how to obtain the following physical properties for a metal:

the phonon linewidths (inverse lifetimes) due to the electron-phonon interaction
the Eliashberg spectral function
the electron-phonon coupling strength
the McMillan critical temperature
the resistivity and electronic part of the thermal conductivity

Here you will learn to use the electron-phonon coupling part of the ANADDB utility. This requires a preliminary calculation of the electron-phonon matrix elements, phonon frequencies and phonon eigenvectors from a standard ABINIT phonon calculation, which we will briefly review.

Note that this tutorial covers a legacy version of the electron-phonon calculation. A new, more efficient workflow is presented in Tutorial Introduction to the new EPH workflow. The old workflow is still useful because it is compatible with spinors (spin orbit coupling), PAW, and therefore also DFT+U, but it will be deprecated at some time in the future.

Visualisation tools are NOT covered in this tutorial. Powerful visualisation procedures have been developed in the Abipy context, relying on matplotlib. See the README of Abipy and the Abipy tutorials.

This tutorial should take about 1 hour.

Note

Supposing you made your own installation of ABINIT, the input files to run the examples are in the ~abinit/tests/ directory where ~abinit is the absolute path of the abinit top-level directory. If you have NOT made your own install, ask your system administrator where to find the package, especially the executable and test files.

In case you work on your own PC or workstation, to make things easier, we suggest you define some handy environment variables by executing the following lines in the terminal:

export ABI_HOME=Replace_with_absolute_path_to_abinit_top_level_dir # Change this line
export PATH=$ABI_HOME/src/98_main/:$PATH      # Do not change this line: path to executable
export ABI_TESTS=$ABI_HOME/tests/             # Do not change this line: path to tests dir
export ABI_PSPDIR=$ABI_TESTS/Pspdir/  # Do not change this line: path to pseudos dir

Examples in this tutorial use these shell variables: copy and paste the code snippets into the terminal (remember to set ABI_HOME first!) or, alternatively, source the set_abienv.sh script located in the ~abinit directory:

source ~abinit/set_abienv.sh

The ‘export PATH’ line adds the directory containing the executables to your PATH so that you can invoke the code by simply typing abinit in the terminal instead of providing the absolute path.

To execute the tutorials, create a working directory (Work*) and copy there the input files of the lesson.

Most of the tutorials do not rely on parallelism (except specific tutorials on parallelism). However you can run most of the tutorial examples in parallel with MPI, see the topic on parallelism.

1 Calculation of the ground state and phonon structure of fcc Al¶

Before beginning, you might consider making a different subdirectory to work in. Why not create Work_eph in $ABI_TESTS/tutorespfn/Input?

It is presumed that the user has already followed the Tutorials RF1 and RF2, and understands the calculation of ground state and response (phonon using density-functional perturbation theory (DFPT)) properties with ABINIT.

Copy the file teph_legacy_1.abi to your working directory. It contains in particular file names and root names for the first run (GS+perturbations).

cd $ABI_TESTS/tutorespfn/Input
mkdir Work_eph
cd Work_eph
cp ../teph_legacy_1.abi .

You can immediately start this run - the input files will be examined later…

abinit teph_legacy_1.abi > log 2> err &

Dataset Structure and Flow¶

The teph_legacy_1.abi file contains a number of datasets (DS). These will perform the ground state (DS 1), then the phonon perturbations (DS 2-4), for a cell of FCC aluminium. The DDK perturbation (DS 5) is also calculated, and will be used to obtain the Fermi velocities for the transport calculations in Section 6.

Once these are done, abinit calculates the wave functions on the full grid of k-points (using kptopt=3) in DS 6: these will be used to calculate the electron-phonon matrix elements. In a full calculation the density of k-points should be increased significantly here and for the following datasets. For DS 1-5 only the normal convergence of the phonon frequencies should be ensured. In DS 7-10 only the matrix elements are calculated, for the electron-phonon coupling and for the DDK (position/momentum matrix elements), on the dense and complete grid of k-points from DS 6. Note that the separation of the matrix element calculation is new from version 7.6.

The important variable for electron-phonon coupling calculations is prtgkk This prints out files suffixed GKK, which contain the electron-phonon matrix elements, and are calculated by DS 7-9. The matrix elements only depend on the self-consistent perturbed density (files suffixed 1DENx), which we get from DS 2-4 (linked by variable get1den). The GKK can therefore be calculated on arbitrarily dense k-point meshes chosen in DS 6. Even better, only a single SCF step is needed, since no self-consistency is required. To enforce the calculation of all the matrix elements on all k-points, symmetries are disabled when prtgkk is set to 1, so be sure not to use it during the normal self-consistent phonon runs DS 2-4. Again this is very different from versions before 7.6.

Convergence¶

The calculation is done using minimal values of a number of parameters, in order to make it tractable in a time appropriate for a tutorial. The results will be completely unconverged, but by the end of the tutorial you should know how to run a full electron phonon calculation, and be able to improve the convergence on your own.

Edit the file teph_legacy_1.abi. We now examine several variables. The kinetic energy cutoff ecut is a bit low, and the number of k-points (determined by ngkpt) is much too low. Electron-phonon calculations require a very precise determination of the Fermi surface of the metal. This implies a very dense k-point mesh, and the convergence of the grid must be checked. In our case, for Al, we will use a (non-shifted) 6x6x6 k-point grid, but a converged calculation needs more than 16x16x16 points. This will be re-considered in section 5. The q-point grid will be 2x2x2, and is selected by the ngqpt, qshift, nqshift, and qptopt variables. It must be a sub-grid of the full k-point grid, and must contain the Γ point. For the phonon and GKK datasets, the q-point is selected by the variable iqpt: this guarantees that there are no errors in transcription of q coordinates, and simplifies workflows. The only unknown ahead of time is the total number of q (and hence datasets) in the irreducible wedge. One way to check this is to set iqpt to a very large value: the error message gives you the size of the irreducible set.

The value of acell is fixed to a rounded value from experiment. It, too, should be converged to get physical results (see Tutorial 3).

Note that the value of 1.0E-14 for tolwfr is tight, and should be even lower (down to 1.0E-20 or even 1.0E-22) for accurate results. This is because the wavefunctions will be used later explicitly in the matrix elements for ANADDB, as opposed to only energy values or densities, which are averages of the wavefunctions and eigenenergies over k-points and bands. Electron-phonon quantities are delicate sums of a few of these small matrix elements (those near the Fermi surface), so each matrix element must be accurate. You can however set prtwf to 0 in the phonon calculations, and avoid saving huge perturbed wavefunction files to disk (you only need to keep the ground state wave functions, with prtwf1 1).

Execution¶

Run the first input (a few seconds on a recent PC), and you should obtain a value of

 etotal -2.3076512079E+00 Ha

for the energy at the end of DATASET 1. The following datasets calculate the second order energy variations under atomic displacement in the three reduced directions of the fcc unit cell. This is done for three different phonons, Gamma, (½,0,0), and X=(½,½,0), which generate the 2x2x2 q-point grid (take care with the reduced coordinates of the reciprocal space points! They are not along cartesian directions, but along the reciprocal space lattice vectors.). The whole calculation follows the same lines as Tutorial RF1. As an example, DATASET 3 calculates the perturbed wavefunctions at k+q, for k in the ground state k-point mesh, and q=(½,0,0). Then, DATASET 3 calculates

 2DTE 6.9410188336E-01 Ha

for the second-order energy variation for movement of the (unique) atom along the first reduced direction for q=(½,0,0). The main differences with Tutorial RF1 are that Given we are dealing with a metal, no perturbation wrt electric fields is considered ; However, if you want to do transport calculations, you need the ddk calculation anyway, to get the electron band velocities. This is added in dataset 5. In the standard case, ABINIT uses symmetry operations and non-stationary expressions to calculate a minimal number of 2DTE for different mixed second derivatives of the total energy. In our case we use the first derivatives, and they must all be calculated explicitly.

You are now the proud owner of 9 first-order matrix element files (suffixed _GKKx, and corresponding copies in netcdf format _GKKx.nc), corresponding to the three directional perturbations of the atom at each of the three q-points. The _GKK files contain the matrix elements of the electron-phonon interaction, which we will extract and use in the following. Besides the _GKK files there are the _DDB files for each perturbation which contain the 2DTE for the different phonons wavevectors q.

2 Merging of the 2DTE DDB files using MRGDDB¶

You can copy the following content to a file teph_legacy_2.abi within your working directory:

teph_legacy_2.ddb.out
Total ddb for Al FCC system
3
teph_legacy_1o_DS2_DDB
teph_legacy_1o_DS3_DDB
teph_legacy_1o_DS4_DDB

or use

This is your input file for the MRGDDB utility, which will take the different _DDB files and merge them into a single one which ANADDB will use to determine the phonon frequencies and eigenvectors. teph_legacy_2.abi contains the name of the final file, a comment line, then the number of _DDB files to be merged and their names. mrgddb is run with the command

 mrgddb < teph_legacy_2.abi

It runs in a few seconds.

3 Extraction and merging of the electron-phonon matrix elements using MRGGKK¶

A merge similar to that in the last section must be carried out for the electron-phonon matrix elements. This is done using the MRGGKK utility, and its input file is $ABI_TESTS/tutorespfn/Input/teph_legacy_3.abi, shown below

teph_legacy_3o_GKK.bin   # Name of output file
0                    # binary (0) or ascii (1) output
teph_legacy_1o_DS1_WFK   # GS wavefunction file
0  9 9               # number of 1WF files, of GKK files, and of perturbations in the GKK files
teph_legacy_1o_DS2_GKK1  # names of the 1WF then the (eventual) GKK files
teph_legacy_1o_DS2_GKK2
...

or use

The matrix element sections of all the _GKK files will be extracted and concatenated into one (binary) file, here named teph_legacy_3o_GKK.bin. The following lines in teph_legacy_3.abi give the output format (0 for binary or 1 for ascii), then the name of the ground state wavefunction file. The fourth line contains 3 integers, which give the number of _1WF files (which can also be used to salvage the GKK), the number of _GKK files, and the number of perturbations in the _GKK files. Thus, MRGGKK functions very much like [help:mrgddb|MRGDDB], and can merge _GKK files which already contain several perturbations (q-points or atomic displacements). Finally, the names of the different _1WF and _GKK files are listed.

MRGGKK will run on this example in a few seconds. In more general cases, the runtime will depend on the size of the system, and for a large number of bands or k-points can extend up to 20 minutes or more.

4 Basic ANADDB calculation of electron-phonon quantities¶

The general theory of electron-phonon coupling and Eliashberg superconductivity is reviewed in Theory of Superconducting Tc, by P.B. Allen and B. Mitrovic. The first implementations similar to that in ABINIT are those in [Savrasov1996] and [Liu1996].

File $ABI_TESTS/tutorespfn/Input/teph_legacy_4.abi contains the input needed by ANADDB to carry out the calculation of the electron-phonon quantities.

ANADDB has file path variables, just like ABINIT, which tells it where to find the input, ddb, and gkk files, and what to name the output, thermodynamical output, and electron phonon output files.

The new variables are at the head of the file:

# turn on calculation of the electron-phonon quantities
elphflag 1

# Path in reciprocal space along which the phonon linewidths
#  and band structure will be calculated
nqpath 7
qpath
 0.0 0.0 0.0
 1/2 1/2 0.0
 1   1   1
 1/2 1/2 1/2
 1/2 1/2 0.0
 1/2 3/4 1/4
 1/2 1/2 1/2

# Coulomb pseudopotential parameter
mustar 0.136

elphflag is a flag to turn on the calculation of the electron- phonon quantities. The first quantities which will be calculated are the phonon linewidths along a path in reciprocal space (exactly like the band structure in the tutorial 3. The path is specified by the variable qpath giving the apexes of the path in reciprocal space, which are usually special points of high symmetry. The number of points is given by nqpath. Note that qpath can be used in normal phonon band structure calculations as well, provided that qph1l is omitted from the input file (the latter overrides qpath). The phonon linewidths are printed to a file suffixed _LWD. The phonon band structure is shown below, and is already stable with a 6x6x6 k-point grid.

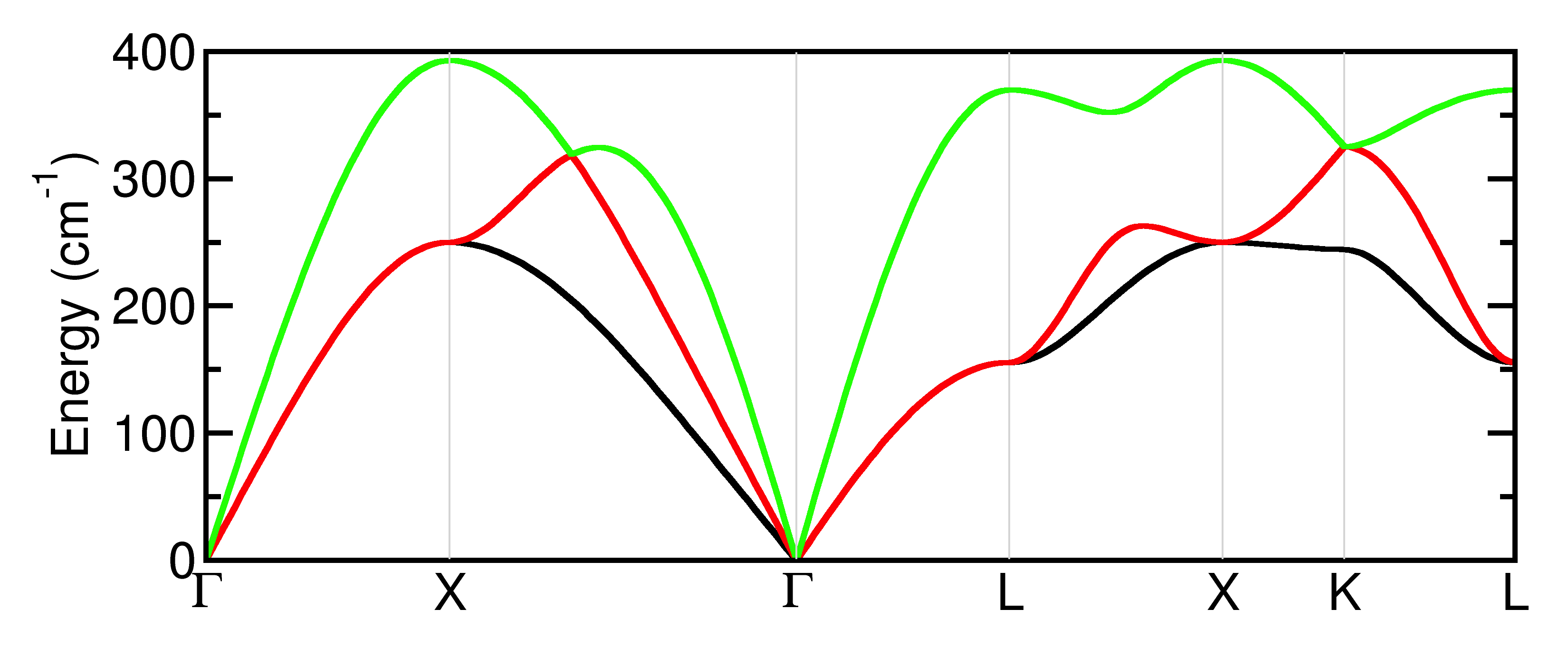
Phonon band structure of Al

The phonon linewidths are proportional to the electron phonon coupling, and still depend on the phonon wavevector q. The other electron-phonon calculations which are presently implemented in ANADDB, in particular for superconductivity, determine isotropic quantities, which are averaged over the Fermi surface and summed over q-points. Integrating the coupling over reciprocal space, but keeping the resolution in the phonon mode’s energy, one calculates the Eliashberg spectral function $\alpha^2F$. The $\alpha^2F$ function is similar to the density of states of the phonons, but is weighted according to the coupling of the phonons to the electrons. It is output to a file with suffix _A2F, which is ready to be represented using any graphical software (Xmgrace, matlab, OpenDX…). The first inverse moment of $\alpha^2F$ gives the global coupling strength, or mass renormalization factor, $\lambda$. From $\lambda$, using the McMillan formula as modified by Allen and Dynes ANADDB calculates the critical temperature for superconductivity. The formula contains an adjustable parameter $\mu^{\star}$ which approximates the effect of Coulomb interactions, and is given by the input variable mustar. For Al with the k-point grid given and a value of $\mu^{\star}$=0.136 the ANADDB output file shows the following values

 mka2f: lambda <omega^2> =     1.179090E-07
 mka2f: lambda <omega^3> =     1.575413E-10
 mka2f: lambda <omega^4> =     2.212559E-13
 mka2f: lambda <omega^5> =     3.213830E-16
 mka2f: isotropic lambda =     8.542685E-02
 mka2f: omegalog  =     1.038371E-03 (Ha)     3.278912E+02 (Kelvin)
 mka2f: input mustar =     1.360000E-01
-mka2f: MacMillan Tc =     2.645390E+05 (Ha)     8.353470E+10 (Kelvin)

As could be expected, this is a very bad estimation of the experimental value of 1.2 K. The coupling strength is severely underestimated (experiment gives 0.44), and the logarithmic average frequency is a bit too high (converged value of 270 K in Savrasov). The resulting critical temperature from McMillan’s formula is unphysical, and you should always regard it critically: if $\lambda$ is close to or lower than the chosen value of $\mu^{\star}$, $T_c$ will diverge. Aluminum is a good case in which things can be improved easily, because its Fermi surface is large and isotropic and the coupling is weak.

5 Convergence tests of the integration techniques¶

In section 4, we used the default method for integration on the Fermi surface, which employs a smearing of the DOS and attributes Gaussian weights to each k-point as a function of its distance from the Fermi surface. Another efficient method of integration in k-space is the tetrahedron method, which is also implemented in ANADDB, and can be used by setting telphint = 0. In this case the k-point grid must be specified explicitly in the input, repeating the variable kptrlatt from the ABINIT output, so that ANADDB can re-construct the different tetrahedra which fill the reciprocal unit cell. In the Gaussian case, the width of the smearing can be controlled using the input variable elphsmear.

To test our calculations, they should be re-done with a denser k-point grid and a denser q-point grid, until the results ($\alpha^2F$ or $\lambda$) are converged. The value of elphsmear should also be checked, to make sure that it does not affect results. Normally, the limit for a very small elphsmear and a very dense k-point grid is the same as the value obtained with the tetrahedron method (which usually converges with a sparser k-point grid).

Edit input file $ABI_TESTS/tutorespfn/Input/teph_legacy_5.abi and you will see the main difference with teph_legacy_4.abi is the choice of the tetrahedron integration method.

Already at this level, you can see the increased accuracy: the isotropic $\lambda$ values (around 0.50) and the MacMillan $T_c$ (2.2 Kelvin) are much more realistic.

If you are patient, save the output _LWD and _A2F files and run the full tutorial again with a denser k-point grid (say, 12x12x12) and you will be able to observe the differences in convergence. For Al the $\alpha^2F$ function and related quantities converge for a minimal k-point grid of about 16x16x16.

6 Transport quantities within Boltzmann theory¶

The electron-phonon interaction is also responsible for the resistivity of normal metals and related phenomena. Even in a perfect crystal, interaction with phonons will limit electron life times (and vice versa). This can be calculated fairly simply using the Boltzmann theory of transport with first order scattering by phonons (see, e.g., “Electrons and Phonons” by Ziman).

The additional ingredient needed to calculate transport quantities (electrical resistivity, heat conductivity limited by electron-phonon coupling) is the Fermi velocity, i.e. the group velocity of a wavepacket of electrons placed at the Fermi surface. This is the “true” velocity the charge will move at, once you have displaced the Fermi sphere a little bit in k space (see, e.g. Ashcroft and Mermin). The velocity can be related simply to a commutator of the position, which is also used for dielectric response, using a DDK calculation (see the first DFPT tutorial (DFPT1). The phonon calculation at Gamma need not include the electric field (this is a metal after all, so the effect on the phonons should be negligible), but we need an additional dataset to calculate the 3 DDK files along the 3 primitive directions of the unit cell. To be more precise, just as for the el-ph matrix elements, we do not need the perturbed wavefunctions, only the perturbed eigenvalues. Calculating the DDK derivatives with prtgkk set to 1 will output files named _GKKxx (xx=3 natom + 1 to 3 natom + 3) containing the matrix elements of the ddk perturbation (these are basically the first part of the normal DDK files for E field perturbation, without the wave function coefficients).

The ANADDB input must specify where the ddk files are, so ANADDB can calculate the Fermi velocities. The variable ddk_filepath points to a small file listing the 3 DDK files to be used, whose contents in our case are:

teph_legacy_1_DS5_GKK4
teph_legacy_1_DS5_GKK5
teph_legacy_1_DS5_GKK6

The abinit input file teph_legacy_1.abi already obtained the DDK files from the additional dataset, DS5, with the following lines of teph_legacy_1.abi:

tolwfr5 1.0d-14
iqpt5 1
rfphon5 0
rfelfd5 2
prtwf5   0

You can copy the additional .ddk file from the tests/tutorespfn/Inputs directory, and run ANADDB. The input for teph_legacy_6.abi has added to teph_legacy_5.abi the following 2 lines:

ifltransport 1
ep_keepbands 1

see

and has produced a number of additional files:

_A2F_TR contain the equivalent Eliashberg spectral functions with Fermi speed factors (how many phonons do we have at a given energy, how much do they couple with the electrons, and how fast are these electrons going). Integrating with appropriate functions of the phonon energy, one gets:
the resistivity as a function of temperature (teph_legacy_6.out_ep_RHO and figure)
the thermal conductivity as a function of temperature (teph_legacy_6.out_ep_WTH) but ONLY the electronic contribution. You are still missing the phonon-phonon interactions, which are the limiting factor in the thermal conductivity beyond a few 100 K. For metals at even higher temperature the electrons will often dominate again as they contain more degrees of freedom.

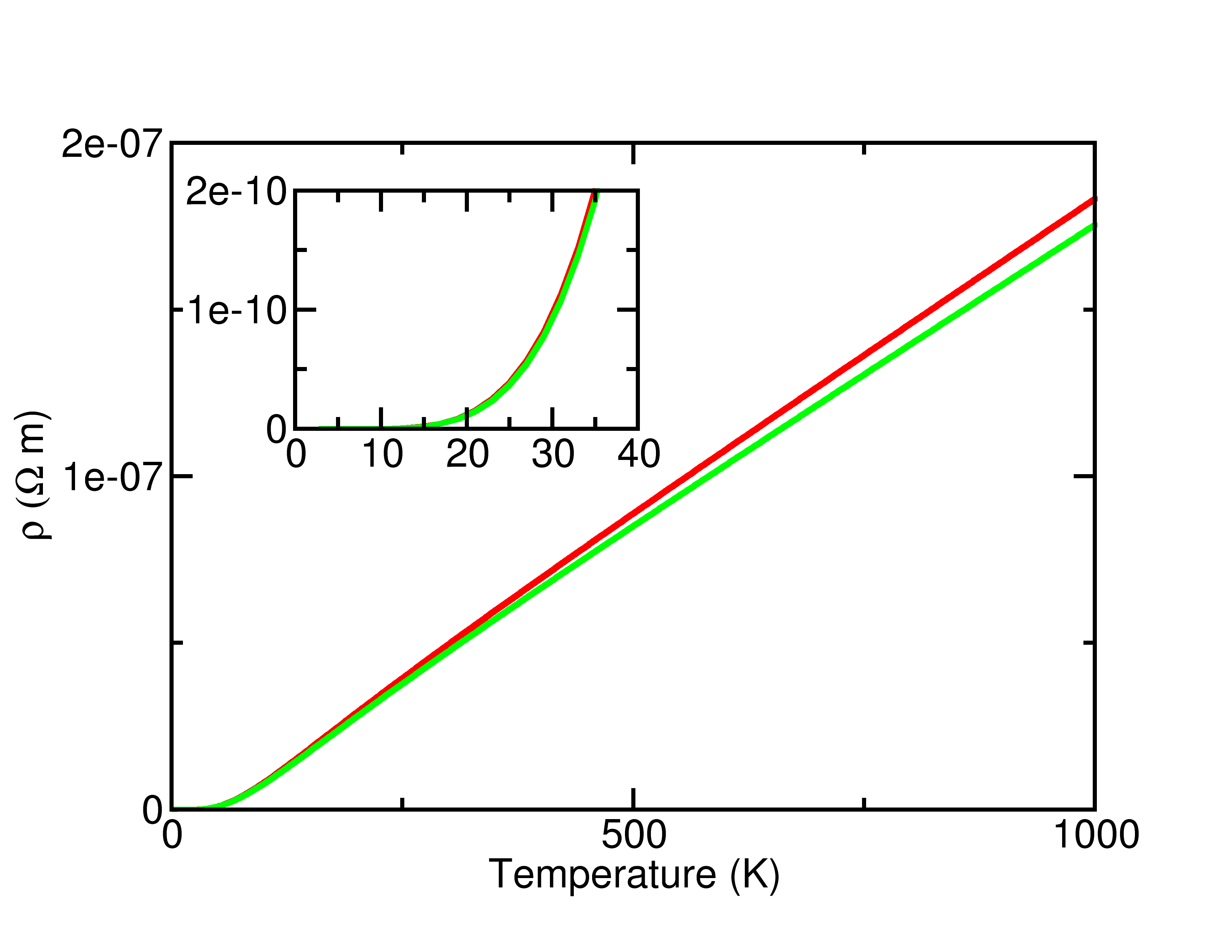
Resistivity of Al as a function of T

The high T behavior is necessarily linear if you include only first order e-p coupling and neglect the variation of the GKK off of the Fermi surface. The inset shows the low T behavior, which is not a simple polynomial (with textbook models it should be T$^3$ or T$^5$ - see Ashcroft and Mermin). See the Savrasov paper for reference values in simple metals using well converged k- and q- point grids, here we are missing a factor of 2, which is not bad given how crude the grids are.

Finally, note that the _RHO and _WTH files contain a series of tensor components, for the resistivity tensor (2 1 = y x or the current response along y when you apply an electric field along x). In many systems the tensor should be diagonal by symmetry, and the value of off-diagonal terms gives an estimate of the symmetrization error (tiny). Similarly the difference in the diagonal terms is due to numerical convergence: here is is a few per-mil, visible in the figure between green and red lines (yy and xx components).