Hubbard U and Hund’s J Parameters with Cococcioni and de Gironcoli’s approach

1 How to determine U and/or J for DFT+U(+J) via Linear Response

This tutorial aims to demonstrate the operations and functionalities of the Abinit post-processing utility called Linear Response Hubbard U and Hund’s J (lruj), designed to determine the first-principles Hubbard U and/or Hund’s J parameters for particular atomic subspaces. Once obtained, these parameters may then be applied via the DFT+U(+J)-like Hubbard functionals to address self-interaction and static correlation errors.

Note that there is another methodology to compute U and J; see the cRPA U(J) tutorial.

In this tutorial, you will learn how to run perturbative calculations in Abinit and generate input data to successfully execute the lruj post-processing utility. We strongly encourage you to read the PAW1, PAW2 and DFT+U tutorials to familiarize yourself with the manifestation of PAW atomic datasets within Abinit. Also consider checking out this video introducing the PAW formalism in an Abinit context.

This tutorial should take less than 30 minutes. We begin with a brief description of the linear response method and an important explanation of recent renovations to the linear response functionalities of Abinit. Click here if you’d like to skip to the NiO tutorial directly.

Note

Supposing you made your own installation of ABINIT, the input files to run the examples are in the ~abinit/tests/ directory where ~abinit is the absolute path of the abinit top-level directory. If you have NOT made your own install, ask your system administrator where to find the package, especially the executable and test files.

In case you work on your own PC or workstation, to make things easier, we suggest you define some handy environment variables by executing the following lines in the terminal:

export ABI_HOME=Replace_with_absolute_path_to_abinit_top_level_dir # Change this line
export PATH=$ABI_HOME/src/98_main/:$PATH      # Do not change this line: path to executable
export ABI_TESTS=$ABI_HOME/tests/             # Do not change this line: path to tests dir
export ABI_PSPDIR=$ABI_TESTS/Psps_for_tests/  # Do not change this line: path to pseudos dir

Examples in this tutorial use these shell variables: copy and paste the code snippets into the terminal (remember to set ABI_HOME first!) or, alternatively, source the set_abienv.sh script located in the ~abinit directory:

source ~abinit/set_abienv.sh

The ‘export PATH’ line adds the directory containing the executables to your PATH so that you can invoke the code by simply typing abinit in the terminal instead of providing the absolute path.

To execute the tutorials, create a working directory (Work*) and copy there the input files of the lesson.

Most of the tutorials do not rely on parallelism (except specific tutorials on parallelism). However you can run most of the tutorial examples in parallel with MPI, see the topic on parallelism.

2 Summary of linear response method to determine U(J)

The Hubbard U and Hund’s J are ground-state properties of any multi-atomic system treated with a given approximate XC functional. They embody the spurious curvature of the total energy with respect to subspace occupation and magnetization respectively. The Hubbard U, specifically, is compensating for an unphysical quadratic term left over by the Hartree energy; it is thus defined as the second derivative of the total energy with respect to charge occupation: $U=\frac{\delta^2 E}{\delta^2 n}$.

Cococcioni and de Gironcoli [Cococcioni2002], following the seminal work from Pickett et al. in 1998 [Pickett1998], further defined a protocol to strictly avoid the semi-empirical evaluation of these parameters. This linear response procedure is described mathematically in terms of constraint formalism and Lagrange coefficients by Dederichs et al. [Dederichs1984] and Anisimov et al. [Anisimov1991]. A formal definition of and analogous procedure for the Hund’s coupling J parameter was published by Linscott et al. in 2018 [Linscott2018].

Practically, the linear response approach begins with the application of a small perturbation $\alpha$($\beta$) to the external potential of the subspace for which U(J) is under assessment. The change in electronic occupation induced by that perturbation is then monitored. This occupational response is, for small perturbations, expected to be a linear function of the perturbation’s magnitude.

Important

For more detailed information on the concepts of the linear response calculation of the Hubbard U and Hund’s J parameters, please see the following papers.

[1] “Linear response approach to the calculation of the effective interaction parameters in the LDA + U method”, M. Cococcioni and S. de Gironcoli, Physical Review B 71, 035105 (2005) [Cococcioni2005]

[2] “The role of spin in the calculation of Hubbard U and Hund’s J parameters from first principles”, E.B. Linscott, D.J. Cole, M.C. Payne and D.D. O’Regan, Physical Review B 98, 235157 (2018) [Linscott2018]

[3] “A LDA+U study of selected iron compounds “, M. Cococcioni, Ph.D. thesis, International School for Advanced Studies (SISSA), Trieste (2002) [Cococcioni2002]

Some further reading:

[4] “Ground States of Constrained Systems: Application to Cerium Impurities”, P. H. Dederichs, S. Blugel, R. Zeller, and H. Akai, Phys. Rev. Lett. 53, 2512 (1984) [Dederichs1984]

[5] “Calculation of Coulomb-interaction parameters for La2CuO4 using a constrained-density-functional approach”, M. S. Hybertsen, M. Schluter, and N. E. Christensen, Phys. Rev. B 39, 9028 (1989) [Hybertsen1989]

[6] “Density-functional calculation of effective Coulomb interactions in metals”, V. I. Anisimov and O. Gunnarsson, Phys. Rev. B42, 7570 (1991) [Anisimov1991]

[7] “Reformulation of the LDA+U method for a local-orbital basis”, W. E. Pickett, S. C. Erwin, and E. C. Ethridge, Phys. Rev. B58, 1201 (1998) [Pickett1998]

The implementation of the determination of U in ABINIT is briefly discussed in [Gonze2016].

3 Renovation of the linear response protocol since Abinit Version 9.6.2

The basic functions of linear response were implemented in Abinit, embedded in its PAW functionality, in 2009. The subsequent U(J) DETermination (ujdet) program was part of the Abinit suite as both an intrinsic DFT protocol and post-processing utility extension. Abinit Version 9.6.2 saw the introduction of an additional macro_uj variable for calculating the Hund’s J with ujdet.

In 2022, users alerted Abinit to the existence of a bug in ujdet which led to the decommission of its post-processing utility and the renovation of its internal Abinit functionality. As of Version 9.6.2, the Abinit DFT suite is equipped with the lruj post-processing tool, which is built off of the same core, but debugged, ujdet programming. Although older versions of Abinit preserve the ujdet internal and post-processing utilities, their use is strongly disadvised. The lruj functionality conserves most of ujdet’s data processing functionalities. For retrogressive and archive purposes, the primary differences between the two are outlined in the table below.

	ujdet	lruj
1	Embedded in Abinit core routine + Post-processing extension	Post-processor
2	Two-point linear regression	3+ point polynomial (variable degree) regression
3	$\chi$ and $\chi_0$ responses treated as matrices; interatomic response monitored; matrices augmented by total system charge	$\chi$ and $\chi_0$ responses treated as scalars
4	Supercell extrapolation scheme	RMS Error analysis
5	Atomic Sphere Approximation projector extensions/normalizations

As mentioned in item (2), the most influential difference between ujdet and lruj is the number of data points used to compute a linear regression of the response functions $\chi$ and $\chi_0$. The ujdet utility uses only two points: the unperturbed case—in which the perturbation applied is zero and the subspace occupations are those of the ground state—and one perturbed case, in which the potential perturbation is equal to the value of pawujv. Note that the ujdet procedure differs slightly from its implementations in Abinit versions prior to 9.6.2, in which it conducted two perturbations: one of strength pawujv and the other of strength -pawujv. Due to a bug in the program, the second perturbation administered provided erroneous unscreened response occupations. To fix this, we exchanged the data point from the second perturbation for one from the unperturbed case, whose occupations are calculated anyway from the ground state wavefunctions read into Abinit.

By contrast, the lruj utility requires, at minimum, three data points (one unperturbed case and at least two perturbations) to conduct a distinctive regression analysis on the response functions. With n data points, the lruj utility computes not only a linear regression, but all polynomial regressions up to degree $n-2$. Furthermore, the lruj utility conducts RMS error analysis on the fits and factors that into an approximative RMS error on the resulting Hubbard parameters.

Another crucial difference between the two utilities is item (3) in the above table: the ujdet utility treats the response functions as matrices, whereas the lruj utility treats them as scalars. Ideologically, this means that the ujdet Hubbard parameters are, to some degree, informed by the Hubbard interactions on and between the other atomic subspaces of the system as well as the total charge bath. The protocol is expanded upon in Cococcioni’s thesis [Cococcioni2002].

By contrast, the lruj utility provides the scalar Hubbard parameters, informed only by the change in occupancy on the perturbed subspace. This parameter is functionally sufficient for SIE corrective application to that subspace.

For all other purposes, it can be said that lruj offers a simplified data processing procedure to that of ujdet. More detailed information is due to follow in the coming months in the form of a user guide, so stay tuned.

4 Determine the Hubbard U for Ni 3d in NiO with lruj

For this tutorial, we will calculate the scalar Hubbard U parameter for the Ni 3d subspace in a four-atom unit cell of AF2-ordered NiO using the lruj post-processing utility. The lruj procedure can be carried out in three steps:

1. Run a ground state Abinit calculation for NiO to generate WFK files.
2. Run a series of perturbative Abinit calculations to generate _LRUJ.nc files.
3. Execute the lruj prost-processing utility.

4.1. Generate the ground-state WFK files

We need to establish a ground state material system whose subspace potential we can perturb. Fortunately, this is principally no different from your standard Abinit ground state run, aside from a few minor modifications to the input file. Make a new work directory called work_lruj, then copy and paste tlruj_1.abi and tlruj_2.abi therein:

cd $ABI_TESTS/tutorial/Input
mkdir work_lruj
cd work_lruj
cp ../tlruj_1.abi .
cp ../tlruj_2.abi .

Important

Henceforth, the name of files are mentioned as if you were in such a subdirectory. All the input files can be found in the $ABI_TESTS/tutorial/Input directory. You can compare your results with the reference output files located in $ABI_TESTS/tutorial/Refs directory (for the prese

Open up tlruj_1.abi; you’ll notice a few key differences between this and other standard ground-state input files.

View tests/tutorial/Input/tlruj_1.abi

First, we specify as a separate species the atom whose subspace we wish to apply a potential perturbation. This will alert Abinit that we want to allow the perturbed Ni 3d subspace to vary its properties independently to the other Ni atom in the cell.

Note

By specifying the perturbed atom as a separate species, Abinit will only harvest the changes in occupation of the perturbed atom. This information is sufficient for the lruj procedure, but not for ujdet. To avail of the supercell extrapolation technique, you will need to set the symmetry relations symrel explicitly. This will tell Abinit that (1) the perturbed atom should vary independently to its kin and (2) it should still collect occupation information for all atoms containing the subspace to be treated, not just that of the perturbed atom. The ujdet utility then uses these interatomic response matrix elements to inform its Hubbard parameters.

You can generate these symmetries in a separate run, wherein you specify the atom upon which the perturbation is to be applied as a different species. From the output, you read the number of symmetries (nsym), the symmetry operations (symrel) and the non-symmorphic vectors (tnons).

Here, we have a four-atom unit cell of NiO. Unlike the ujdet utility, the lruj utility can accomodate the perturbation of any Ni atom in the cell. For right now, we apply a perturbation to the first Ni atom by making the following modifications:

           Original                              Modified
-------------------------------     -------------------------------
ntypat = 2                          ntypat = 3
typat = 1 1 2 2                     typat = 1 2 3 3
znucl = 28 8                        znucl = 28 28 8
pseudos = “Ni.xml,O.xml”            pseudos = “Ni.xml,Ni.xml,O.xml”

If you are using other input variables whose dimensions are set by ntypat, you will need to change those as well.

Note

If using the ujdet functionality that performs the supercell extrapolation schema, the perturbation should only be applied to the first atom listed in xred. Make sure that the coordinates of the perturbed atom are listed first.

Since the Hubbard parameters are ground state properties of your choice XC functional, it is discouraged to make this a DFT+U(J) run in which U(J) are non-zero. Therefore, we add the following to the script

usepawu 1
lpawu 2 2 1
upawu 0.0 0.0 0.0 eV
jpawu 0.0 0.0 0.0 eV

and ensure that prtwf is set to 1 so that the WFK file is printed. The lpawu 2 setting specifies the $3d$ orbitals on Ni as those for which we will calculate and apply U.

Other related variables include a high tolvrs = 10d-11 so that we can converge the electronic structure to a high degree of accuracy. The ecut is chosen to be very low in order to accelerate calculations, so raise this for precision calculations. All other variables used to conduct a ground state calculation remain unmodified. Launch the Abinit run to print out the WFK file.

abinit tlruj_1.abi > tlruj_1.log

The run should take about a minute to run, but times vary depending on your hardware. This concludes Step 1.

4.2. Linear response perturbations and generation of LRUJ.nc files

Once we have our reference wavefunctions, we can start the linear response procedure, which we summon and guide via the following additional input variables in tlruj_2.abi:

• pawujv => Strength of the perturbation (usually on the order of 10e-1 to 10e-2). Default value is 0.1 eV. (Our tests show that 0.1 eV is the optimal value, but the linear response is linear in a wide range (1-0.001 eV).)
• macro_uj => With nsppol, which parameter is Abinit to determine? For nsppol = 2, set macro_uj to 1 for Hubbard U, or set macro_uj to 4 for the Hund’s J.

It is typically enough to make macro_uj non-zero. To run a perturbative calculation for the Hubbard U parameter, we set macro_uj to 1 and nsppol to 2. Note also, that the irdwfk 1 and the tolvrs 1d-8 do not need to be set explicitly because they are the defaults with a non-zero macro_uj. Lastly, ensure that the variable pawujat, which identifies the perturbed atom, is set to the same atom specified as a separate species in generating the WFK file.

Note

When irdwfk is set to 1, Abinit is instructed to read in the WFK files for a prior run given the files are named according to a specific convention. Alternatively, we can specify the WFK file and its path by name with the following:

irdwfk 0
getwfk_filepath "</pathtofile/filename_WFK>"

In changing only these variables, we set up only one perturbative calculation. This is sufficient to avail of the ujdet utility functionalities, which require only two data points as discussed above. However, in many, if not all, cases, one perturbation is inadequate to compute a good regression of the linear response data, and no error analysis can be conducted thereof.

For this reason, we will need to conduct several (at minimum four, although the more, the better) perturbative calculations. We will take advantage of Abinit’s dataset function to get our system to iteratively undergo n perturbations by setting ndtset to n and then specifying which perturbation strengths pawujv1, pawujv2, … , pawujvn we would like to apply. In this tutorial specifically, we take n to be 5 and vary the perturbation magnitude between -0.15 eV and 0.10 eV. Take a look at tlruj_2.abi to visualize this description.

View tests/tutorial/Input/tlruj_2.abi

To manage the print volume related to the ujdet functions, set pawprtvol and prtvol. All other variables remain unmodified. Launch the Abinit run to print out the *_LRUJ.nc files.

abinit tlruj_2.abi > tlruj_2.log

This more expensive calculation should take under five minutes to run. Open up the output file.

View tests/tutorial/Refs/tlruj_2.abo

You will find all information related to the calculation of the U parameter between the calculate U, (J) flags. The first information printed out is as follows:

*********************************************************************
************************  Linear Response U  ************************

 Info printed for perturbed atom:    1

  Perturbations           Occupations
 --------------- -----------------------------
    alpha [eV]     Unscreened      Screened
 --------------- -----------------------------
   0.0000000000   8.6380190174   8.6380190174
  -0.1500000000   8.6964896369   8.6520721437

                    Scalar response functions:
                    Chi0 [eV^-1]:     -0.86623
                    Chi [eV^-1]:      -0.09369

 The scalar U from the two-point regression scheme is   9.51936 eV.
*********************************************************************
*********************************************************************

Here, ujdet lists out the perturbation strengths and their corresponding unscreened and screened occupations. (When calculating the Hund’s J, Occupations will be replaced by Magnetizations.) From here, the scalar response functions $\chi$ and $\chi_0$ are printed out, followed by the scalar definition of U in units of eV. By scalar, we mean that the response functions are treated as scalars, and thus the U printed here is informed only by the occupational responses on the perturbed atom.

The lines starting with URES, by contrast, report the U as a function of its inverted (and charge bath augmented) response matrices:

 URES      ii    nat       r_max    U(J)[eV]   U_ASA[eV]   U_inf[eV]
 URES       1      1     0.00000     2.37984     1.91514     1.85257
 URES       2      8    11.14400     8.34413     6.71480     6.49545
 URES       3     27    12.45940     9.16724     7.37718     7.13619
 URES       4     64    22.28800     9.37065     7.54088     7.29454
 URES       5    125    24.28780     9.44321     7.59926     7.35102
 URES       6    216    33.43200     9.47529     7.62508     7.37599

These values of U are computed using the extrapolation procedure proposed in [Cococcioni2005]. In this work, it is shown that using a two atom supercell for the DFT calculation and an extrapolation procedure can yield an estimation of the value of U. More precise values can be and often are obtained by running linear response DFT calculations on larger and larger supercells. This procedure succeeds in isolating the perturbed subspace from its periodic images.

The column nat indicates how many atoms were involved in the extrapolated supercell, and r_max indicates the maximum distance of the perturbed atom from its periodic images. The column U(J) reports in eV the calculated values of the Hubbard parameters that should then be applied via the Hubbard functionals. U_ASA and U_inf are estimates of U for more extended projectors; they are related to the charge population analysis conducted under the PAW method and controlled by variable dmatpuopt.

This is the information printed out for one perturbation of strength pawujv; five further perturbations are conducted, for each of which the same information is printed in the output file. You should have five *_LRUJ.nc files in your directory, which we will use as input for the lruj post-processing utility to determine a better estimate of the U parameter.

4.3. Execution of the lruj post-processinng utility

Once the _LRUJ.nc files are printed, execute the lruj utility (found in the same directory as the abinit executable) with the following command.

lruj *_LRUJ.nc > tlruj_lruj.out

It should take less than a second to run. If the lruj utility runs successfully, the resulting output file, tlruj_lruj.out, should look like this:

View tests/tutorial/Refs/tlruj_3.stdout

This specific calculation looks at the Hubbard U parameter (macro_uj 1) using results from five (5) perturbations, the strengths of which are listed in the first table alongside the corresponding subspace occupations, both unscreened (for $\chi_0$, harvested during the first SCF cycle, immediately after the perturbation is applied but before the Hamiltonian is updated) and screened (for $\chi$, harvested from the SCF converged subspaces occupancies).

  Perturbations           Occupations
 --------------- -----------------------------
    alpha [eV]     Unscreened      Screened
 --------------- -----------------------------
  -0.1500000676   8.6964981921   8.6520721998
  -0.1000000451   8.6747201574   8.6474287212
  -0.0500000225   8.6560314462   8.6427490201
   0.0000000000   8.6380182458   8.6380182458
   0.0500000225   8.6192514478   8.6332174978
   0.1000000451   8.5980252003   8.6283148749

The last table gives the values for $\chi_0$, $\chi$, the Hubbard U, and their RMS errors in units of eV, for all polynomial regressions up to degree 3 (cubic).

                                                                     RMS Errors
                                                         ---------------------------------------
 Regression   Chi0 [eV^-1]   Chi [eV^-1]      U [eV]    | Chi0 [eV^-1]  Chi [eV^-1]     U [eV]
--------------------------------------------------------|---------------------------------------
 Linear:        -0.8594082    -0.0949434     9.3689968  |    0.0023925    0.0000878    0.0029335
 Quadratic:     -0.8574665    -0.0955791     9.2963113  |    0.0023777    0.0000129    0.0027762
 Cubic:         -0.8007858    -0.0952726     9.2474280  |    0.0001546    0.0000015    0.0001937

One has the option of calculating higher order polynomials, up to degree $n–2$ for n points. This is done by appending the degree option –d followed by an integer to the command line. For example, for polynomial regressions up to degree 4 of the above calculation with 6 data points, try bashing

lruj *_LRUJ.nc --d 4 > tlruj_lruj_d4.out

to get the following output:

                                                                       RMS Errors
                                                         ---------------------------------------
 Regression   Chi0 [eV^-1]   Chi [eV^-1]      U [eV]    | Chi0 [eV^-1]  Chi [eV^-1]     U [eV]
--------------------------------------------------------|---------------------------------------
 Linear:        -0.8594082    -0.0949434     9.3689968  |    0.0023925    0.0000878    0.0029335
 Quadratic:     -0.8574665    -0.0955791     9.2963113  |    0.0023777    0.0000129    0.0027762
 Cubic:         -0.8007858    -0.0952726     9.2474280  |    0.0001546    0.0000015    0.0001937
 Degree 4 :     -0.8049062    -0.0952279     9.2587427  |    0.0000790    0.0000003    0.0000981

Note

The lruj program will only calculate polynomials up to degree $n–2$ for n data points; so, by default, if one reads in only two _LRUJ.nc files, the maximum polynomial regression conducted will be linear; three _LRUJ.nc files means maximum degree is quadratic, and so on. Other command line options for the lruj utility include –version and –help.

The values in eV of the Hubbard U parameter according to each regression are found in column four. To assess which one is best, you’ll want to use the RMS errors in column seven. Furthermore, you can import the perturbation/occupation table into Excel (or any other choice of graphical utility) to visualize the fits. The following graph visualizes our data in Mathematica.

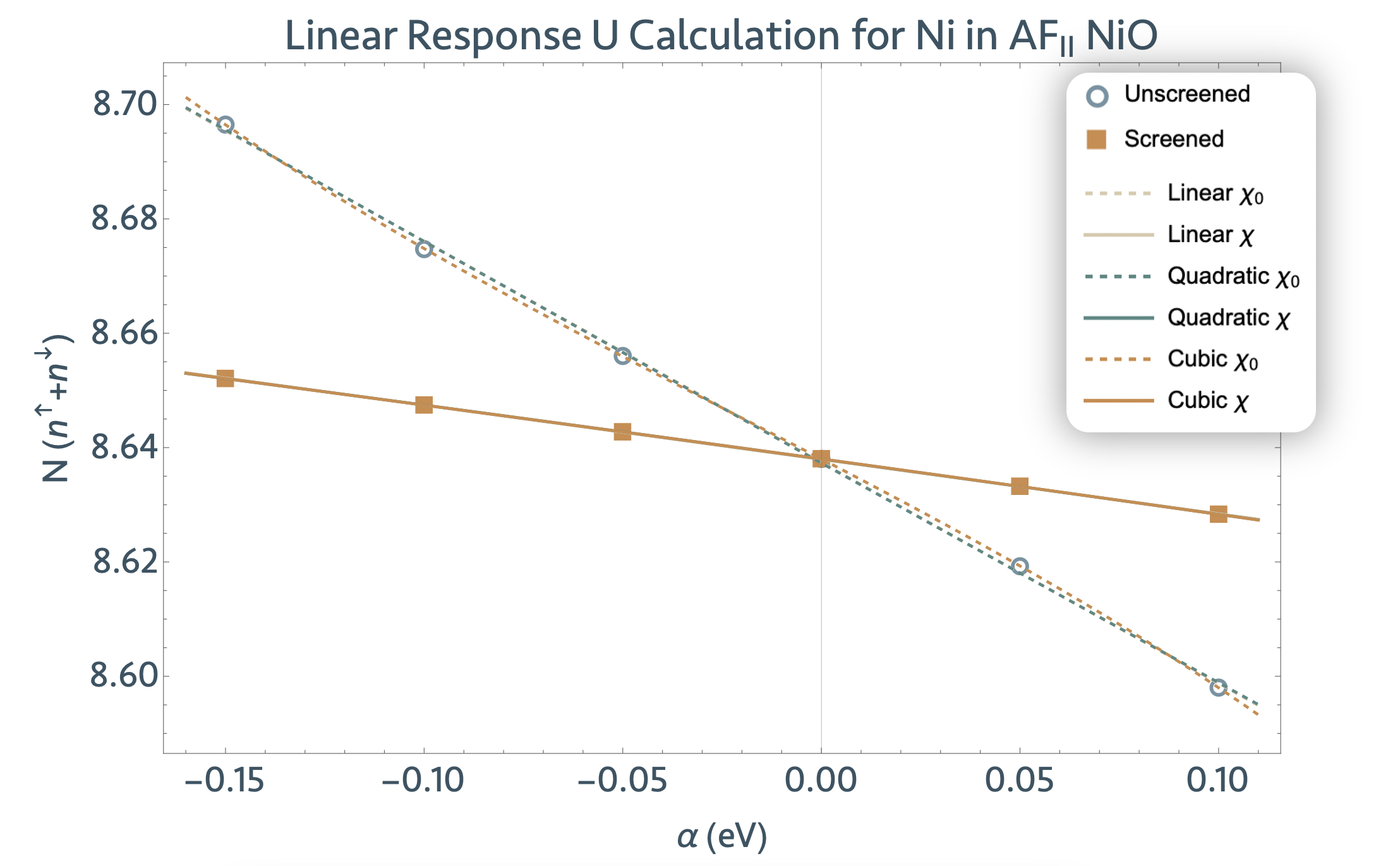
Based on this information, one could argue the quadratic fit is sufficient. Thus, we get a first-principles Hubbard U value of 9.296 ± 0.003 eV for the Ni 3d subspace in a four-atom cell of AF2 NiO. This is much larger than values for NiO reported in the literature values, which can be attributed to the poor ecut and ngkpt sampling needed to speed up this tutorial. Furthermore, this indicates that these parameters must be converged with respect to supercell size in order to isolate the perturbed subspace from its periodic images.

Repeating Steps 1-3 with macro_uj set to 4 will give us the Hund’s J parameter for the same Ni 3d subspaces. We do this now but more precisely, doubling the value of ecut and lowering the tolerance, etc. When we plot the linear response data, it becomes more obvious why more scruitnous run parameters are necessary and why polynomials of higher order are needed to perform an accurate regression:

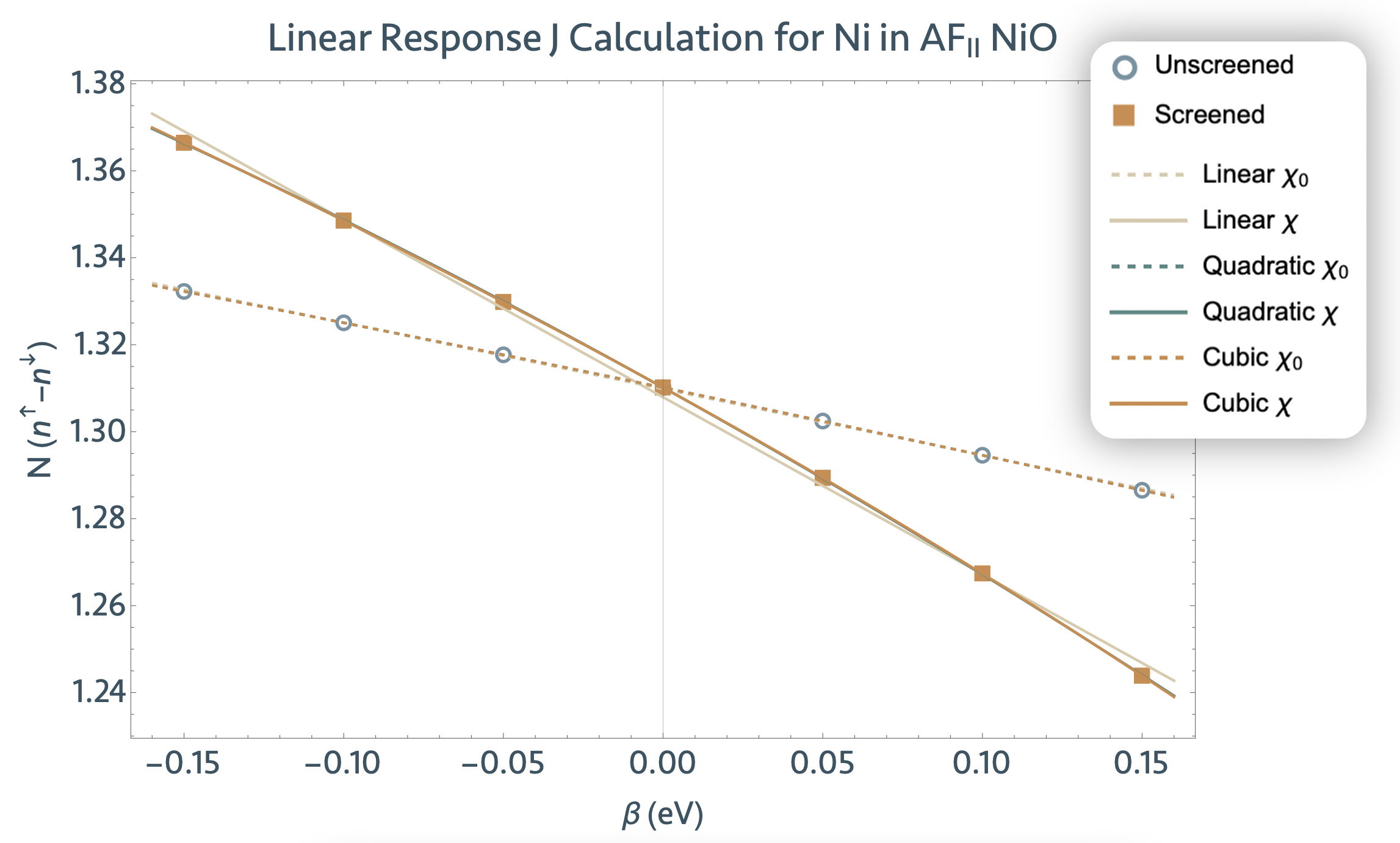
Here, we see that the quadratic fit, at minimum, sufficiently fits the data, yielding a Hund’s J value of 0.4994 ± 0.0004 eV for the Ni 3d subspace in a four-atom cell NiO. Keep in mind, however, that these parameters MUST be converged with respect to supercell size in order to isolate the perturbed subspace from its periodic images.