Second tutorial on the Projector Augmented-Wave (PAW) technique¶
Generation of PAW atomic datasets¶
This tutorial aims at showing how to create your own atomic datasets for the Projector Augmented-Wave (PAW) method.
You will learn how to generate these atomic datasets and how to control their softness and transferability. You already should know how to use ABINIT in the PAW case (see the tutorial PAW1 ).
This tutorial should take about 2h00.
Note
Supposing you made your own installation of ABINIT, the input files to run the examples are in the ~abinit/tests/ directory where ~abinit is the absolute path of the abinit top-level directory. If you have NOT made your own install, ask your system administrator where to find the package, especially the executable and test files.
In case you work on your own PC or workstation, to make things easier, we suggest you define some handy environment variables by executing the following lines in the terminal:
export ABI_HOME=Replace_with_absolute_path_to_abinit_top_level_dir # Change this line
export PATH=$ABI_HOME/src/98_main/:$PATH # Do not change this line: path to executable
export ABI_TESTS=$ABI_HOME/tests/ # Do not change this line: path to tests dir
export ABI_PSPDIR=$ABI_TESTS/Pspdir/ # Do not change this line: path to pseudos dir
Examples in this tutorial use these shell variables: copy and paste
the code snippets into the terminal (remember to set ABI_HOME first!) or, alternatively,
source the set_abienv.sh script located in the ~abinit directory:
source ~abinit/set_abienv.sh
The ‘export PATH’ line adds the directory containing the executables to your PATH so that you can invoke the code by simply typing abinit in the terminal instead of providing the absolute path.
To execute the tutorials, create a working directory (Work*) and
copy there the input files of the lesson.
Most of the tutorials do not rely on parallelism (except specific tutorials on parallelism). However you can run most of the tutorial examples in parallel with MPI, see the topic on parallelism.
1. The PAW atomic dataset - introduction¶
The PAW method is based on the definition of spherical augmentation regions of radius \(r_c\) around the atoms of the system in which a basis of atomic partial-waves \(\phi_i\), of pseudized partial-waves \(\tphi_i\), and of projectors \(\tprj_i\) (dual to \(\tphi_i\)) have to be defined. This set of partial-waves and projectors functions (and some additional atomic data) are stored in a so-called PAW dataset. A PAW dataset has to be generated for each atomic species in order to reproduce atomic behavior as accurate as possible while requiring minimal CPU and memory resources in executing ABINIT for the crystal simulations. These two constraints are obviously conflicting.
The PAW dataset generation is the purpose of this tutorial. It is done according the following procedure (all parameters that define a PAW dataset are in bold):
-
Choose and define the concerned chemical species (name and atomic number).
-
Solve the atomic all-electrons problem in a given atomic configuration. The atomic problem is solved within the DFT formalism, using an exchange-correlation functional and either a Schrodinger (default) or scalar-relativistic approximation. This spherical problem is solved on a radial grid. The atomic problem is solved for a given electronic configuration that can be an ionized/excited one.
-
Choose a set of electrons that will be considered as frozen around the nucleus (core electrons). The others electrons are valence ones and will be used in the PAW basis. The core density is then deduced from the core electrons wave functions. A smooth core density equal to the core density outside a given \(r_{core}\) matching radius is computed.
-
Choose the size of the PAW basis (number of partial-waves and projectors). Then choose the partial-waves included in the basis. The later can be atomic eigen-functions related to valence electrons (bound states) and/or additional atomic functions, solution of the wave equation for a given \(l\) quantum number at arbitrary reference energies (unbound states).
-
Generate pseudo partial-waves (smooth partial-waves build with a pseudization scheme and equal to partial-waves outside a given \(r_c\) matching radius) and associated projector functions. Pseudo partial-waves are solutions of the PAW Hamiltonian deduced from the atomic Hamiltonian by pseudizing the effective potential (a local pseudopotential is built and equal to effective potential outside a $r_{Vloc} matching radius). Projectors and partial-waves are then orthogonalized with a chosen orthogonalization scheme.
-
Build a compensation charge density used later in order to retrieve the total charge of the atom. This compensation charge density is located inside the PAW spheres and based on an analytical shape function (which analytic form and localization radius \(r_{shape}\) can be chosen).
The user can choose between two PAW dataset generators to produce atomic files directly readable by ABINIT.
The first one is the PAW generator ATOMPAW (originally by N. Holzwarth) and
the second one is the Ultra-Soft USPP generator (originally written by D. Vanderbilt). In this tutorial, we concentrate only on ATOMPAW.
It is highly recommended to refer to the following papers to understand correctly the generation of PAW atomic datasets:
-
“Projector augmented-wave method” - [Bloechl1994]
-
“A projector Augmented Wave (PAW) code for electronic structure” - [Holzwarth2001]
-
“From ultrasoft pseudopotentials to the projector augmented-wave method” - [Kresse1999]
-
“Electronic structure packages: two implementations of the Projector Augmented-Wave (PAW) formalism” - [Torrent2010]
-
“Notes for revised form of atompaw code” (by N. Holzwarth) - PDF
2. Use of the generation code¶
Before continuing, you might consider to work in a different subdirectory as
for the other tutorials. Why not Work_paw2?
cd $ABI_TESTS/tutorial/Input
mkdir Work_paw2
cd Work_paw2
You have now to install the ATOMPAW code. In your internet browser, enter the following URL:
https://users.wfu.edu/natalie/papers/pwpaw/
Then, download the last version of the tar.gz file, unzip and untar it.
Enter the atompaw-4.x.y.z and execute:
mkdir build
cd build
../configure
make
if all goes well, you get the ATOMPAW executable at
atompaw-4.x.y.z/build/src/atompaw.
If not, Go into the directory doc, open the file atompaw-usersguide.pdf, go p.3 and follow the instructions.
Note
On MacOS, you can use homebrew package manager and install ATOMPAW by typing:
brew install atompaw/repo/atompaw
Note
In the following, we name atompaw the ATOMPAW executable.
How to use ATOMPAW?
The following process will be applied to Nickel in the next paragraph:
- Edit an input file in a text editor (content of input explained here)
- Run: atompaw < inputfile
Partial waves \(\phi_i\), PS partial-waves \(\tphi_i\) and projectors \(\tprj_i\) are given in wfn.i files.
Logarithmic derivatives from atomic Hamiltonian and PAW Hamiltonian
resolutions are given in logderiv.l files.
A summary of the atomic all-electron computation and PAW dataset properties
can be found in the Atom_name file (Atom_name is the first parameter of the input file).
Resulting PAW dataset is contained in:
-
Atom_name.XCfunc.xmlfile Normalized XML file according to the PAW- XML specifications (recommended). -
Atom_name.XCfunc-paw.abinitfile Proprietary legacy format for ABINIT
3. First (and basic) PAW dataset for Nickel¶
Our test case will be nickel; electronic configuration: \([1s^2 2s^2 2p^6 3s^2 3p^6 3d^8 4s^2 4p^0]\).
In a first stage, copy a simple input file for ATOMPAW in your working directory
(find it in $ABI_HOME/doc/tutorial/paw2/paw2_assets/Ni.atompaw.input1).
Edit this file.
Ni 28 ! Definition of material GGA-PBE scalarrelativistic loggrid 2000 ! All-electrons calc.: GGA+scalar-relativstic - log.grid with 2000 pts 4 4 3 0 0 0 ! Max. n per angular momentum: 4s 3p 3d 3 2 8 ! Partially occupied states: 3d: occ=8 4 1 0 ! 4p: occ=0 0 0 0 ! End of occupation section c ! 1s: core state c ! 2s: core state c ! 3s: core state v ! 4s: valence state c ! 2p: core state c ! 3p: core state v ! 4p: valence state v ! 3d: valence state 2 ! Max. l for partial waves basis 2.3 ! r_PAW radius y ! Do we add an additional s partial wave ? yes 0.5 ! Reference energy for this new s partial wave (Ryd) n ! Do we add an additional s partial wave ? no y ! Do we add an additional p partial wave ? yes 1. ! Reference energy for this p new partial wave (Ryd) n ! Do we add an additional p partial wave ? no y ! Do we add an additional d partial wave ? yes 0. ! Reference energy for this new d partial wave (Ryd) n ! Do we add an additional s partial wave ? no bloechl ! Scheme for PS partial waves and projectors 3 0. troulliermartins ! Scheme for pseudopotential (l_loc=3, E_loc=0Ry) XMLOUT ! Option for XML dataset creation default ! All parameters set to default for XML dataset END ! End of file
This file has been built in the following way:
- All-electron calculation parameters:
- 1st line: define the material.
Ni 28 - 2nd line: choose the exchange-correlation functional (LDA-PW or GGA-PBE)
and select a scalar-relativistic wave equation
(nonrelativistic or scalarrelativistic)
and a (2000 points) logarithmic grid.
GGA-PBE scalarrelativistic loggrid 2000
- 1st line: define the material.
-
Electronic configuration: How many electronic states do we need to include in the computation? Besides the fully and partially occupied states, it is recommended to add all states that could be reached by electrons in the solid. Here, for Nickel, the \(4p\) state is concerned. So we decide to add it in the computation.
- 3rd line: define the electronic configuration.
A line with the maximum \(n\) quantum number for each electronic shell; here
4 4 3means4s, 4p, 3d.4 4 3 0 0 0 - Following lines : definition of occupation numbers.
For each partially occupied shell enter the occupation number.
An excited configuration may be useful if the PAW dataset is intended for use in a
context where the material is charged (such as oxides). Although, in our
experience, the results are not highly dependent on the chosen electronic configuration.
We choose here the \([3d^8 4s^2 4p^0]\) configuration.
Only \(3d\) and \(4p\) shells are partially occupied (
3 2 8and4 1 0lines). A0 0 0ends the occupation section.3 2 8 4 1 0 0 0 0
- 3rd line: define the electronic configuration.
A line with the maximum \(n\) quantum number for each electronic shell; here
-
Selection of core and valence electrons. In a first approach, select only electrons from outer shells as valence. But, if particular thermodynamical conditions are to be simulated, it is generally needed to include “semi-core states” in the set of valence electrons. Semi-core states are generally needed with transition metal and rare-earth materials. Note that all wave functions designated as valence electrons will be used in the partial-wave basis. Core shells are designated by a \(c\) and valence shells by a \(v\). All \(s\) states first, then \(p\) states and finally \(d\) states. Here:
means:c c c v c c v v1s core 2s core 3s core 4s valence 2p core 3p core 4p valence 3d valence - Partial-waves basis generation:
- A line with \(l_{max}\) the maximum \(l\) for
the partial-waves basis. Here \(l_{max}=2\).
2 - A line with the \(r_{PAW}\) radius.
Select it to be slightly less than half the inter-atomic distance
in the solid (as a first choice). Here \(r_{PAW}=2.3\ a.u\).
2.3 - Next lines: add additional partial-waves \(\phi_i\) if needed.
Choose to have 2 partial-waves per angular momentum in the basis (this choice is not
necessarily optimal but this is the most common one; if \(r_{PAW}\) is small enough,
1 partial-wave per \(l\) may suffice).
As a first guess, put
all reference energies
for additional partial-waves to 0 Rydberg.
For each angular momentum, first add “y” to add an additional partial-wave.
Then, next line, put the value in Rydberg units.
Repeat this for each new partial-wave and finally put “n”.
Note : For each angular momentum, valence states already are included in
the partial-waves basis. Here \(4s\), \(4p\) and \(3d\) states already are in the basis.
In the present file:
means that an additional \(s\)- partial-wave at \(E_{ref}=0.5\) Ry as been added,
y 0.5 nmeans that an additional \(p\)- partial-wave at \(E_{ref}=1.\) Ry has been added,y 1. nmeans that an additional \(d\)- partial-wave at \(E_{ref}=1.\) Ry as been added. Finally, partial-waves basis contains two \(s\)-, two \(p\)- and two \(d\)- partial-waves.y 1. n - Next line: definition of the generation scheme for pseudo partial
waves \(\tphi_i\), and of projectors \(\tprj_i\).
We begin here with a simple scheme (i.e. “Bloechl” scheme, proposed by P. Blochl [Bloechl1994]).
This will probably be changed later to make the PAW dataset more efficient.
bloechl - Next line: generation scheme for local pseudopotential
\(V_{loc}\). In order to get PS partial-waves, the atomic potential has to be “pseudized”
using an arbitrary pseudization scheme.
We choose here a “Troullier-Martins” using a wave equation at \(l_{loc}=3\) and \(E_{loc}=0.\) Ry.
As a first draft, it is always recommended to put \(l_{loc}=1+l_{max}\).
3 0. troulliermartins - Next two lines:
XMLOUTmakesATOMPAWgenerate a PAW dataset in XML format; The next line contains options for this ABINIT file. “default” set all parameters to their default value.XMLOUT default - The
ENDkeyword ends the file.END
- A line with \(l_{max}\) the maximum \(l\) for
the partial-waves basis. Here \(l_{max}=2\).
At this stage, run ATOMPAW. For this purpose, simply enter:
atompaw < Ni.atompaw.input1
Lot of files are produced. We will examine some of them.
A summary of the PAW dataset generation process has been written in a file
named Ni.
Open it. It should look like:
Completed calculations for Ni
Exchange-correlation type: GGA, Perdew-Burke-Ernzerhof
Radial integration grid is logarithmic
r0 = 2.2810899E-04 h = 6.3870518E-03 n = 2000 rmax = 8.0000000E+01
Scalar relativistic calculation
AEatom converged in 32 iterations
for nz = 28.00
delta = 9.5504321957145377E-017
All Electron Orbital energies:
n l occupancy energy
1 0 2.0000000E+00 -6.0358607E+02
2 0 2.0000000E+00 -7.2163318E+01
3 0 2.0000000E+00 -8.1627107E+00
4 0 2.0000000E+00 -4.1475541E-01
2 1 6.0000000E+00 -6.2083048E+01
3 1 6.0000000E+00 -5.2469208E+00
4 1 0.0000000E+00 -9.0035739E-02
3 2 8.0000000E+00 -6.5223644E-01
Total energy
Total : -3041.0743834110435
Completed calculations for Ni
Exchange-correlation type: GGA, Perdew-Burke-Ernzerhof
Radial integration grid is logarithmic
r0 = 2.2810899E-04 h = 6.3870518E-03 n = 2000 rmax = 8.0000000E+01
Scalar relativistic calculation
SCatom converged in 1 iterations
for nz = 28.00
delta = 8.7786021384577619E-017
Valence Electron Orbital energies:
n l occupancy energy
4 0 2.0000000E+00 -4.1475541E-01
4 1 0.0000000E+00 -9.0035739E-02
3 2 8.0000000E+00 -6.5223644E-01
Total energy
Total : -3041.0743834029249
Valence : -185.18230020196870
paw parameters:
lmax = 2
rc = 2.3096984974114871
irc = 1445
Vloc: Norm-conserving Troullier-Martins with l= 3;e= 0.0000E+00
Projector type: Bloechl + Gram-Schmidt ortho.
Sinc^2 compensation charge shape zeroed at rc
Number of basis functions 6
No. n l Energy Cp coeff Occ
1 4 0 -4.1475541E-01 -9.5091487E+00 2.0000000E+00
2 999 0 5.0000000E-01 3.2926948E+00 0.0000000E+00
3 4 1 -9.0035739E-02 -8.9594191E+00 0.0000000E+00
4 999 1 1.0000000E+00 1.0610645E+01 0.0000000E+00
5 3 2 -6.5223644E-01 9.1576184E+00 8.0000000E+00
6 999 2 0.0000000E+00 1.3369076E+01 0.0000000E+00
Completed diagonalization of ovlp with info = 0
Eigenvalues of overlap operator (in the basis of projectors):
1 7.27257365E-03
2 2.25491432E-02
3 1.25237568E+00
4 1.87485118E+00
5 1.05720648E+01
6 2.00807906E+01
Summary of PAW energies
Total valence energy -185.18230536120760
Smooth energy 11.667559552612433
One center -196.84986491382003
Smooth kinetic 15.154868503980399
Vloc energy -2.8094614733964467
Smooth exch-corr -3.3767012052640886
One-center xc -123.07769380742522
The generated PAW dataset (contained in Ni.GGA-PBE.xml file) is a first draft. Several parameters have to be adjusted, in order to get accurate results and efficient DFT calculations.
Note
The Ni.GGA-PBE.xml file is directly usable by ABINIT.
4. Checking the sensitivity to some parameters¶
4.a. The radial grid¶
Let’s try to select 700 points in the logarithmic grid and check if any noticeable
difference in the results appears.
You just have to replace 2000 by 700 in the second line of Ni.atompaw.input1 file.
Then run:
atompaw < Ni.atompaw.input1
again and look at the Ni file:
Summary of PAW energies
Total valence energy -185.18230027710337
Smooth energy 11.634042318422193
One center -196.81634259552555
Smooth kinetic 15.117782033814152
Vloc energy -2.8024659321861067
Smooth exch-corr -3.3712015132649102
One-center xc -123.08319475096027
As you see, results obtained with this new grid are very close to previous ones, expecially the valence energy.
We can keep the 700 points grid.
Note
We could try to decrease the size of the grid. Small grids give PAW dataset with small size (in kB) and run faster in ABINIT, but accuracy can be affected.
Note
The final \(r_{PAW}\) value (rc = ... in Ni file) changes with the
grid; just because \(r_{PAW}\) is adjusted in order to belong exactly to the radial grid.
By looking in ATOMPAW user’s guide, you can choose to keep it constant.
4.b. The relativistic approximation of the wave equation¶
The scalar-relativistic option should give better results than non-relativistic one, but it sometimes produces difficulties for the convergence of the atomic problem (either at the all-electron resolution step or at the PAW Hamiltonian solution step). If convergence cannot be reached, try a non-relativistic calculation (not recommended for high Z materials).
Note
For the following, note that you always should check the Ni file, especially
the values of valence energy. You can find the valence energy
computed for the exact atomic problem and the valence energy computed with the
PAW parameters. These two results should be in close agreement!
5. Adjusting partial-waves and projectors¶
Examine the AE partial-waves \(\phi_i\), PS partial-waves \(\tphi_i\) and projectors \(\tprj_i\).
These are saved in files named wfni, where i ranges over the number of partial-waves
used, so 6 in the present example.
Each file contains 4 columns: the radius \(r\) in column 1,
the AE partial-wave \(\phi_i(r)\) in column 2, the PS partial-wave \(\tphi_i(r)\) in
column 3, and the projector \(\tprj_i(r)\) in column 4.
Plot the 3 curves as a function of radius using a plotting tool of your choice.
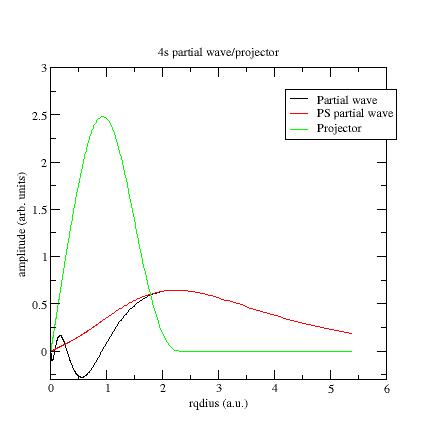
Below the first \(s\)- partial-wave /projector of the Ni example:
-
\(\phi_i\) should meet \(\tphi_i\) near or after the last maximum (or minimum). If not, it is preferable to change the value of the matching (pseudization) radius \(r_c\).
-
The maxima of \(\tphi_i\) and \(\tprj_i\) functions should roughly have the same order of magnitude. If not, you can try to get this in three ways:
- Change the matching radius for this partial-wave; but this is not always possible (PAW spheres should not overlap in the solid).
- Change the pseudopotential scheme (see later).
- If there are two (or more) partial-waves for the angular momentum \(l\) under consideration, decreasing the magnitude of the projector is possible by displacing the references energies. Moving the energies away from each other generally reduces the magnitude of the projectors, but too big a difference between energies can lead to wrong logarithmic derivatives (see following section).
Example: plot the wfn6 file, related to the second \(d\)- partial-wave:

This partial-wave has been generated at \(E_{ref}=0\) Ry and orthogonalized with the
first \(d\)- partial-wave which has an eigenenergy equal to \(-0.65\) Ry (see Ni file).
These two energies are too close and orthogonalization process produces “high” partial-waves.
Try to replace the reference energy for the additional \(d\)- partial-wave.
For example, put \(E_{ref}=1.\) Ry instead of \(E_{ref}=0.\) Ry (line 24 of Ni.atompaw.input1 file).
Run ATOMPAW again and plot wfn6 file:

Now the PS partial-wave and projector have the same order of magnitude!
Important
Note again that you should always check the two Valence energy values in Ni file and make
sure they are as close as possible.
If not, choices for projectors and/or partial-waves are certainly not judicious.
6. Examine the logarithmic derivatives¶
Examine the logarithmic derivatives, i.e., derivatives of an \(l\)-state
\(\frac{d(log(\Psi_l(E))}{dE}\) computed for the exact atomic problem and with the PAW dataset.
They are printed in the logderiv.l files. Each logderiv.l file corresponds to an
angular momentum \(l\) and contains five columns of data: the
energy, the logarithmic derivative of the \(l\)-state of the exact atomic problem,
the logarithmic derivative of the pseudized problem (and two other colums not relevant for this section). In the following, when you edit a logderiv file, only edit the three first columns.
In our Ni example, \(l=0\), \(1\) or \(2\).
The logarithmic derivatives should have the following properties:
-
The 2 curves should be superimposed as much as possible. By construction, they are superimposed at the 2 energies corresponding to the 2 \(l\) partial-waves. If the superimposition is not good enough, the reference energy for the second \(l\) partial-wave should be changed.
-
Generally a discontinuity in the logarithmic derivative curve appears at \(0\) Ry \(\le E_0\le 4\) Ry. A reasonable choice is to choose the 2 reference energies so that \(E_0\) is in between.
-
Too close reference energies produce “hard” projector functions (see section 5). But moving reference energies away from each other can damage accuracy of logarithmic derivatives
Here are the three logarithmic derivative curves for the current dataset:
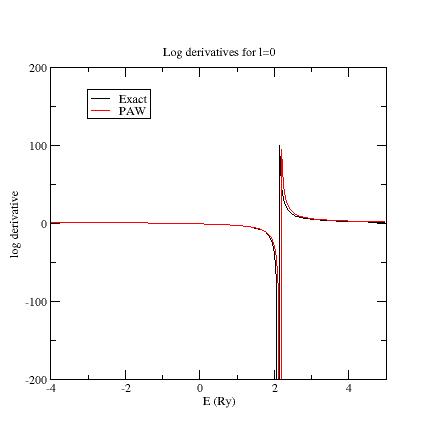


As you can see, except for \(l=2\), exact and PAW logarithmic derivatives do not match!
According to the previous remarks, try other values for the references
energies of the \(s\)- and \(p\)- additional partial-waves.
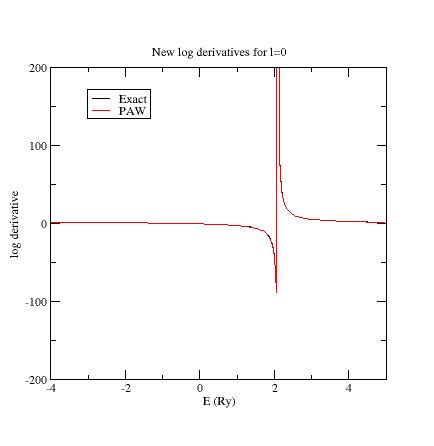
First, edit again the Ni.atompaw.input1 file and put \(E_{ref}=3\) Ry for the
additional \(s\)- state (line 18); run ATOMPAW again. Plot the logderiv.0 file.
You should get:
Then put \(E_{ref}=4\) Ry for the second \(p\)- state (line 21); run ATOMPAW again.
Plot again the logderiv.1 file.
You should get:
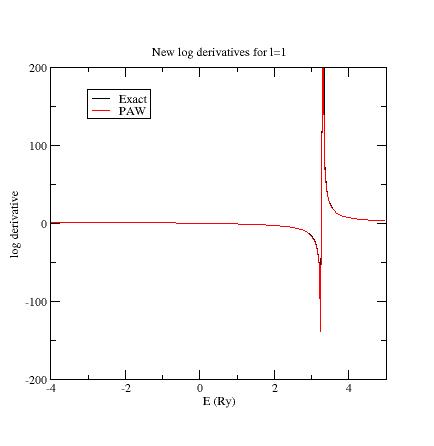
Now, all PAW logarithmic derivatives match with the exact ones in a reasonable interval.
Note
It is possible to change the interval of energies used to plot logarithmic
derivatives (default is \([-5;5]\)) and also to compute them at more points
(default is \(200\)). Just add the following keywords at the end of the SECOND
LINE of the input file if you want ATOMPAW to output logarithmic derivatives
for energies in [-10;10] at 500 points:
logderivrange -10 10 500
Additional information related to logarithmic derivatives: ghost states
Another possible issue could be the presence of a discontinuity in the PAW logarithmic derivative curve at an energy where the exact logarithmic derivative is continuous. This generally shows the presence of a ghost state.
- First, try to change to value of reference energies; this sometimes can make the ghost state disappear.
- If not, it can be useful to change the pseudopotential scheme. Norm-conserving pseudopotentials are
sometimes too attractive near \(r=0\).
- A 1st solution is to change the quantum number used to generate the norm-conserving pseudopotential. But this is generally not sufficient.
- A 2nd solution is to select a
ultrasoftpseudopotential, freeing the norm conservation constraint (simply replacetroulliermartinsbyultrasoftin the input file). - A 3rd solution is to select a simple
besselpseudopotential (replacetroulliermartinsbybesselin the input file). But, in that case, one has to noticeably decrease the matching radius \(r_{Vloc}\) if one wants to keep reasonable physical results. Selecting a value of \(r_{Vloc}\) between \(0.6~r_{PAW}\) and \(0.8~r_{PAW}\) is a good choice. To change the value of \(r_{Vloc}\), one has to explicitely put all matching radii: \(r_{PAW}\), \(r_{shape}\), \(r_{Vloc}\) and \(r_{core}\); see user’s guide.
- Last solution : try to change the matching radius \(r_c\) for one (or both) \(l\) partial-wave(s). In some cases, changing \(r_c\) can remove ghost states.
In most cases (changing pseudopotential or matching radius), one has to restart the procedure from step 5.
To see an example of ghost state, use the
$ABI_HOME/doc/tutorial/paw2_assets/Ni.ghost.atompaw.input file and run it with ATOMPAW.
Ni 28 GGA-PBE scalarrelativistic loggrid 1500 4 4 3 0 0 0 4 0 1 4 1 0 3 2 9 0 0 0 c c c v c c v v 2 2.0 2.0 2.0 2.0 y 4. n y 4. n y 1. n vanderbilt 3 0. troulliermartins 2.0 2.0 2.0 2.0 2.0 2.0 XMLOUT default END
Look at the \(l=1\) logarithmic derivatives (logderiv.1 file). They look like:
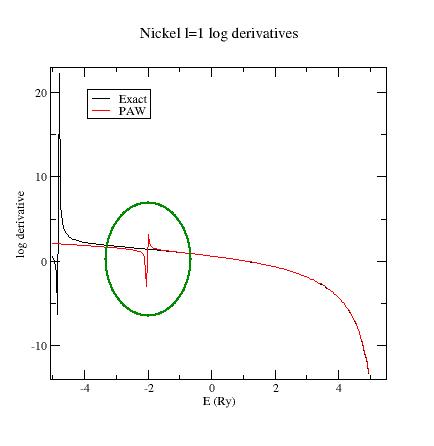
Now, edit the Ni.ghost.atompaw.input file and replace troulliermartins by
ultrasoft.
Run ATOMPAW again… and look at logderiv.1 file.
The ghost state has moved!
Edit again the file and replace troulliermartins by bessel (line 28); then change the 17th
line 2.0 2.0 2.0 2.0 by 2.0 2.0 1.8 2.0 (decreasing the \(r_{Vloc}\) radius from \(2.0\) to \(1.8\)).
Run ATOMPAW: the ghost state disappears!
Start from the original state of Ni.ghost.atompaw.input file and put 1.6 for
the matching radius of \(p\)- states (put 1.6 on lines 31 and 32).
Run ATOMPAW: the ghost state disappears!
7. Testing the “efficiency” of a PAW dataset¶
Let’s use again our Ni.atompaw.input1 file for Nickel (with all our modifications). You get a file Ni.GGA-PBE-paw.xml containing the PAW dataset designed for ABINIT.
To test the efficiency of the generated PAW dataset, we finally will use ABINIT!
You are about to run a DFT computation and determine the size of the plane
wave basis needed to reach a given accuracy. If the cut-off energy defining the
plane waves basis is too high (higher than 20 Hartree), some changes have to be made in the input file.
Copy $ABI_TESTS/tutorial/Input/tpaw2_1.abi in your working directory.
Edit it, and activate the 8 datasets (uncomment the line ndtset 8).
# Input for PAW2 tutorial # Nickel ferromagnetic fcc structure # Testing ecut convergence #Define the different datasets #ndtset 8 # 8 datasets. Uncomment this line for the tutorial ndtset 1 # 1 datasets. Comment this line for the tutorial ecut: 8. # The starting values of the plane-wave cut-off energy ecut+ 2. # The increment of ecut from one dataset to the other getwfk -1 # The starting wave-functions are those of the previous dataset #------------------------------------------------------------------------------- #The rest of this file defines the parameters cmmon to all datasets #Definition of the unit cell acell 3*3.52 angstrom # Lengths of the primitive vectors (angstrom) rprim # 3 orthogonal primitive vectors (FCC lattice) 0.0 1/2 1/2 1/2 0.0 1/2 1/2 1/2 0.0 nsym 0 # Automatic detection of symetries #Definition of the atom types and pseudopotentials ntypat 1 # There is only one type of atom znucl 28 # Atomic number of the possible type(s) of atom. Here Nickel. pp_dirpath "$ABI_PSPDIR" # Path to the directory were # pseudopotentials for tests are stored pseudos "Ni.PBE-paw.bloechl.xml" # Name and location of the pseudopotential #Definition of the atoms natom 1 # There is one atom typat 1 # It is of type 1, that is, Nickel xred # Location of the atom: 0.0 0.0 0.0 # Triplet giving the reduced coordinates of atom #Definition of bands and occupation numbers nband 14 # Compute 14 bands nsppol 2 # We perform a spin-polarized calculations (nickel is magnetic) spinat 0. 0. 4. # Initial spin for the atom (high value to "push" the calculation) occopt 7 # Automatic generation of occupation numbers, as a metal tsmear 0.0075 # Smearing temperature for the metallic occupation scheme (Hartree) #Numerical parameters of the calculation : planewave basis set and k point grid ecut 12.0 # Maximal plane-wave kinetic energy cut-off, in Hartree (not used here) pawecutdg 40. # Max. plane-wave kinetic energy cut-off, in Ha, for the PAW double grid kptopt 1 # Automatic generation of k points, taking into account the symmetry ngkpt 6 6 6 # This is a 6x6x6 grid based on the primitive vectors nshiftk 4 # of the reciprocal space, repeated four times, shiftk # with different shifts: 0.5 0.5 0.5 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.5 #Parameters for the SCF procedure nstep 35 # Maximal number of SCF cycles tolvrs 1.0d-9 # Will stop when, twice in a row, the difference # between two consecutive evaluations of potential residual # differ by less than tolvrs #Miscelaneous parameters prtwf 1 # Print wavefunctions (re-used from one dataset to the other) prtden 0 # Do not print density prteig 0 # Do not print eigenvalues ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tpaw2_1.abo, tolnlines= 13, tolabs= 1.1e-2, tolrel= 5.0e-1, fld_options=-medium #%% output_file = "tpaw2_1.abo" #%% [paral_info] #%% max_nprocs = 6 #%% [extra_info] #%% authors = M. Torrent #%% keywords = PAW #%% description = #%% Input for PAW2 tutorial #%% Nickel ferromagnetic fcc structure #%% Testing ecut convergence #%%<END TEST_INFO>
Run ‘ABINIT’. It computes the total energy of ferromagnetic FCC Nickel for several values of ecut.
At the end of output file, you get this:
ecut1 8.00000000E+00 Hartree
ecut2 1.00000000E+01 Hartree
ecut3 1.20000000E+01 Hartree
ecut4 1.40000000E+01 Hartree
ecut5 1.60000000E+01 Hartree
ecut6 1.80000000E+01 Hartree
ecut7 2.00000000E+01 Hartree
ecut8 2.20000000E+01 Hartree
etotal1 -3.9299840066E+01
etotal2 -3.9503112955E+01
etotal3 -3.9582704516E+01
etotal4 -3.9613343901E+01
etotal5 -3.9622927015E+01
etotal6 -3.9626266739E+01
etotal7 -3.9627470087E+01
etotal8 -3.9627833090E+01
etotal convergence (at 1 mHartree) is achieve for \(18 \le e_{cut} \le 20\) Hartree.
etotal convergence (at 0,1 mHartree) is achieve for \(e_{cut} \ge 22\) Hartree.
This is not a good result for a PAW dataset; let’s try to optimize it.
- 1st possibility: use
vanderbiltprojectors instead ofbloechlones. Vanderbilt’s projectors generally are more localized in reciprocal space than Bloechl’s ones . Keywordbloechlhas to be replaced byvanderbiltin theATOMPAWinput file and \(r_c\) values have to be added at the end of the file (one for each PS partial-wave). See this input file: $ABI_HOME/doc/tutorial/paw2_assets/Ni.atompaw.input.vanderbilt.
Ni 28 ! Definition of material GGA-PBE scalarrelativistic loggrid 700 ! All-electrons calc.: GGA+scalar-relativstic - log.grid with 700 pts 4 4 3 0 0 0 ! Max. n per angular momentum: 4s 3p 3d 3 2 8 ! Partially occupied states: 3d: occ=8 4 1 0 ! 4p: occ=0 0 0 0 ! End of occupation section c ! 1s: core state c ! 2s: core state c ! 3s: core state v ! 4s: valence state c ! 2p: core state c ! 3p: core state v ! 4p: valence state v ! 3d: valence state 2 ! Max. l for partial waves basis 2.3 ! r_PAW radius y ! Do we add an additional s partial wave ? yes 3. ! Reference energy for this new s partial wave (Ryd) n ! Do we add an additional s partial wave ? no y ! Do we add an additional p partial wave ? yes 4. ! Reference energy for this p new partial wave (Ryd) n ! Do we add an additional p partial wave ? no y ! Do we add an additional d partial wave ? yes 1. ! Reference energy for this new d partial wave (Ryd) n ! Do we add an additional s partial wave ? no vanderbilt ! Scheme for PS partial waves and projectors 3 0. troulliermartins ! Scheme for pseudopotential (l_loc=3, E_loc=0Ry) 2.2 ! r_c matching radius for first s partial wave 2.2 ! r_c matching radius for second s partial wave 2.3 ! r_c matching radius for first p partial wave 2.3 ! r_c matching radius for second p partial wave 2.3 ! r_c matching radius for first d partial wave 2.3 ! r_c matching radius for second d partial wave XMLOUT ! Option for XML dataset creation default ! All parameters set to default for XML dataset END ! End of file
- 2nd possibility: use
RRKJpseudization scheme for projectors. Use this input file forATOMPAW: $ABI_HOME/doc/tutorial/paw2_assets/Ni.atompaw.input2. As you can seebloechlhas been changed bycustom rrkjand six \(r_c\) values have been added at the end of the file, each one corresponding to the matching radius of one PS partial-wave. Repeat the entire procedure (ATOMPAW+ABINIT)… and get a new ABINIT output file. Note: You have check again log derivatives.
Ni 28 ! Definition of material GGA-PBE scalarrelativistic loggrid 700 ! All-electrons calc.: GGA+scalar-relativstic - log.grid with 700 pts 4 4 3 0 0 0 ! Max. n per angular momentum: 4s 3p 3d 3 2 8 ! Partially occupied states: 3d: occ=8 4 1 0 ! 4p: occ=0 0 0 0 ! End of occupation section c ! 1s: core state c ! 2s: core state c ! 3s: core state v ! 4s: valence state c ! 2p: core state c ! 3p: core state v ! 4p: valence state v ! 3d: valence state 2 ! Max. l for partial waves basis 2.3 ! r_PAW radius y ! Do we add an additional s partial wave ? yes 3. ! Reference energy for this new s partial wave (Ryd) n ! Do we add an additional s partial wave ? no y ! Do we add an additional p partial wave ? yes 4. ! Reference energy for this p new partial wave (Ryd) n ! Do we add an additional p partial wave ? no y ! Do we add an additional d partial wave ? yes 1. ! Reference energy for this new d partial wave (Ryd) n ! Do we add an additional s partial wave ? no custom rrkj ! Scheme for PS partial waves and projectors 3 0. troulliermartins ! Scheme for pseudopotential (l_loc=3, E_loc=0Ry) 2.2 ! r_c matching radius for first s partial wave 2.2 ! r_c matching radius for second s partial wave 2.3 ! r_c matching radius for first p partial wave 2.3 ! r_c matching radius for second p partial wave 2.3 ! r_c matching radius for first d partial wave 2.3 ! r_c matching radius for second d partial wave XMLOUT ! Option for XML dataset creation default ! All parameters set to default for XML dataset END ! End of file
ecut1 8.00000000E+00 Hartree
ecut2 1.00000000E+01 Hartree
ecut3 1.20000000E+01 Hartree
ecut4 1.40000000E+01 Hartree
ecut5 1.60000000E+01 Hartree
ecut6 1.80000000E+01 Hartree
ecut7 2.00000000E+01 Hartree
ecut8 2.20000000E+01 Hartree
etotal1 -3.9599860476E+01
etotal2 -3.9626919903E+01
etotal3 -3.9627249378E+01
etotal4 -3.9627836846E+01
etotal5 -3.9628304332E+01
etotal6 -3.9628429611E+01
etotal7 -3.9628436662E+01
etotal8 -3.9628455467E+01
etotal convergence (at 1 mHartree) is achieve for \(12 \le e_{cut} \le 14\) Hartree.
etotal convergence (at 0,1 mHartree) is achieve for \(16 \le e_{cut} \le 18\) Hartree.
This is a reasonable result for a PAW dataset!
- 3rd possibility: use enhanced polynomial pseudization scheme for projectors.
Edit
Ni.atompaw.input2
and replace
custom rrkjbycustom polynom2 7 10. It may sometimes improve the ecut convergence.
Optional exercise¶
Let’s go back to Vanderbilt projectors.
Repeat the procedure (ATOMPAW + ABINIT) with the previous
\Ni.atompaw.input.vanderbilt file.
Ni 28 ! Definition of material GGA-PBE scalarrelativistic loggrid 700 ! All-electrons calc.: GGA+scalar-relativstic - log.grid with 700 pts 4 4 3 0 0 0 ! Max. n per angular momentum: 4s 3p 3d 3 2 8 ! Partially occupied states: 3d: occ=8 4 1 0 ! 4p: occ=0 0 0 0 ! End of occupation section c ! 1s: core state c ! 2s: core state c ! 3s: core state v ! 4s: valence state c ! 2p: core state c ! 3p: core state v ! 4p: valence state v ! 3d: valence state 2 ! Max. l for partial waves basis 2.3 ! r_PAW radius y ! Do we add an additional s partial wave ? yes 3. ! Reference energy for this new s partial wave (Ryd) n ! Do we add an additional s partial wave ? no y ! Do we add an additional p partial wave ? yes 4. ! Reference energy for this p new partial wave (Ryd) n ! Do we add an additional p partial wave ? no y ! Do we add an additional d partial wave ? yes 1. ! Reference energy for this new d partial wave (Ryd) n ! Do we add an additional s partial wave ? no vanderbilt ! Scheme for PS partial waves and projectors 3 0. troulliermartins ! Scheme for pseudopotential (l_loc=3, E_loc=0Ry) 2.2 ! r_c matching radius for first s partial wave 2.2 ! r_c matching radius for second s partial wave 2.3 ! r_c matching radius for first p partial wave 2.3 ! r_c matching radius for second p partial wave 2.3 ! r_c matching radius for first d partial wave 2.3 ! r_c matching radius for second d partial wave XMLOUT ! Option for XML dataset creation default ! All parameters set to default for XML dataset END ! End of file
Let’s try to change the pseudization scheme for the local pseudopotential.
Try to replace the troulliermartins keyword by ultrasoft.
Repeat the procedure (ATOMPAW + ABINIT).
ABINIT can now reach convergence!
Results are below:
ecut1 8.00000000E+00 Hartree
ecut2 1.00000000E+01 Hartree
ecut3 1.20000000E+01 Hartree
ecut4 1.40000000E+01 Hartree
ecut5 1.60000000E+01 Hartree
ecut6 1.80000000E+01 Hartree
ecut7 2.00000000E+01 Hartree
ecut8 2.20000000E+01 Hartree
etotal1 -3.9608001348E+01
etotal2 -3.9613479343E+01
etotal3 -3.9616615528E+01
etotal4 -3.9620665403E+01
etotal5 -3.9622873734E+01
etotal6 -3.9623393021E+01
etotal7 -3.9623440787E+01
etotal8 -3.9623490997E+01
etotal convergence (at 1 mHartree) is achieve for \(14 \le e_{cut} \le 16\) Hartree.
etotal convergence (at 0,1 mHartree) is achieve for \(20 \le e_{cut} \le 22\) Hartree.
Note
You could have tried the bessel keyword instead of ultrasoft one.
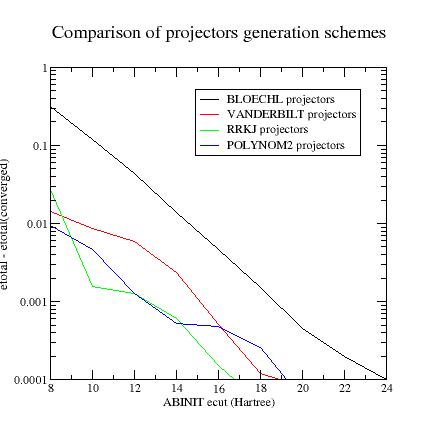
Summary of convergence results
Final_remarks
-
The localization of projectors in reciprocal space can (generally) be predicted by a look at
tprod.ifiles. Such a file contains the curve of as a function of \(q\) (reciprocal space variable). \(q\) is given in \(Bohr^{-1}\) units; it can be connected to ABINIT plane waves cut-off energy (in Hartree units) by: \(e_{cut}=\frac{q_{cut}^2}{4}\). These quantities are only calculated for the bound states, since the Fourier transform of an extended function is not well-defined. -
Generating projectors with Blochl’s scheme often gives the guaranty to have stable calculations.
ATOMPAWends without any convergence problem and DFT calculations run without any divergence (but they need high plane wave cut-off). Vanderbilt projectors (and even morecustomprojectors) sometimes produce instabilities during the PAW dataset generation process and/or the DFT calculations but are more efficient. -
In most cases, after having changed the projector generation scheme, one has to restart the procedure from step 5.
8 Testing against physical quantities¶
The last step is to examine carefully the physical quantities obtained with our PAW dataset.
Copy $ABI_TESTS/tutorial/Input/tpaw2_2.abi in your working directory. Edit it, activate the 7 datasets (ubcomment the ‘ndtset 7` line), and use $ABI_HOME/doc/tutorial/paw2_assets/Ni.PBE-paw.rrkj.xml PAW dataset obtained from Ni.atompaw.input2 file, with a minor change of name (suppression of the indication GGA). Run ABINIT (this may take a while…).
# Input for PAW2 tutorial # Nickel ferromagnetic fcc structure # Testing ecut convergence #Define the different datasets #ndtset 7 # 7 datasets. Uncomment this line for the tutorial ndtset 1 # 1 datasets. Comment this line for the tutorial acell: 3*3.5150 angstrom # The starting values of the cell parameters acell+ 3*0.0025 angstrom # The increment of acell from one dataset to the other getwfk -1 # The starting wave-functions are those of the previous dataset #------------------------------------------------------------------------------- #The rest of this file defines the parameters cmmon to all datasets #Definition of the unit cell acell 3*3.52 angstrom # Lengths of the primitive vectors (angstrom) rprim # 3 orthogonal primitive vectors (FCC lattice) 0.0 1/2 1/2 1/2 0.0 1/2 1/2 1/2 0.0 nsym 0 # Automatic detection of symetries #Definition of the atom types and pseudopotentials ntypat 1 # There is only one type of atom znucl 28 # Atomic number of the possible type(s) of atom. Here Nickel. pp_dirpath "$ABI_PSPDIR" # Path to the directory were # pseudopotentials for tests are stored pseudos "Ni.PBE-paw.rrkj.xml" # Name and location of the pseudopotential #Definition of the atoms natom 1 # There is one atom typat 1 # It is of type 1, that is, Nickel xred # Location of the atom: 0.0 0.0 0.0 # Triplet giving the reduced coordinates of atom #Definition of bands and occupation numbers nband 12 # Compute 12 bands nsppol 2 # We perform a spin-polarized calculations (nickel is magnetic) spinat 0. 0. 4. # Initial spin for the atom (high value to "push" the calculation) occopt 7 # Automatic generation of occupation numbers, as a metal tsmear 0.0075 # Smearing temperature for the metallic occupation scheme (Hartree) #Numerical parameters of the calculation : planewave basis set and k point grid ecut 15.0 # Maximal plane-wave kinetic energy cut-off, in Hartree (not used here) pawecutdg 40. # Max. plane-wave kinetic energy cut-off, in Ha, for the PAW double grid ecutsm 0.5 # Introduce a smooth PW cutoff within an 0.5 Ha region kptopt 1 # Automatic generation of k points, taking into account the symmetry ngkpt 8 8 8 # This is a 8x8x8 grid based on the primitive vectors nshiftk 4 # of the reciprocal space, repeated four times, shiftk # with different shifts: 0.5 0.5 0.5 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.5 #Parameters for the SCF procedure nstep 35 # Maximal number of SCF cycles tolvrs 1.0d-12 # Will stop when, twice in a row, the difference # between two consecutive evaluations of potential residual # differ by less than tolvrs #Miscelaneous parameters prtwf 1 # Print wavefunctions (re-used from one dataset to the other) prtden 0 # Do not print density prteig 0 # Do not print eigenvalues fftalg 112 # This impose the use of ABINIT internal FFT # This is only to numerically stabilize the results # and make them more reproducible (in terms of the number of # SCF iterations). But it could affect the performances. # !! !Please, do not put this keyword this in normal use. ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tpaw2_2.abo, tolnlines= 18, tolabs= 1.1e-1, tolrel= 5.0e-1, fld_options=-easy #%% output_file = "tpaw2_2.abo" #%% [paral_info] #%% max_nprocs = 6 #%% [extra_info] #%% authors = M. Torrent #%% keywords = PAW #%% description = #%% Input for PAW2 tutorial #%% Nickel ferromagnetic fcc structure #%% Testing ecut convergence #%%<END TEST_INFO>
<?xml version="1.0"?> <paw_dataset version="0.7"> <!-- PAW-XML specification: http://esl.cecam.org/Paw-xml --> <atom symbol="Ni" Z="28.00" core="18.00" valence="10.00"/> <xc_functional type="GGA" name="PBE"/> <generator type="scalar-relativistic" name="atompaw-4.1.0.6" orthogonalisation="gramschmidt"/> <!-- Atompaw 4.1.0.6 Contact info: Natalie Holzwarth email: natalie@wfu.edu, web: pwpaw.wfu.edu Energy units=Hartree, length units=bohr PAW functions generated on 03/24/2020, 11:46:41.157 The input file is available at the end of this file Atompaw --> <ae_energy kinetic=" 1.54165686916885920E+03" xc=" -6.32271980146899395E+01" electrostatic=" -2.99896687173672990E+03" total=" -1.52053720058255476E+03"/> <core_energy kinetic=" 1.46734502120880052E+03"/> <paw_radius rc=" 2.31145012469019"/> <valence_states> <state n=" 4" l="0" f=" 2.0000000E+00" rc=" 2.2347172798" e="-2.0737773E-01" id= "Ni1"/> <state l="0" rc=" 2.2347172798" e=" 1.5000000E+00" id= "Ni2"/> <state n=" 4" l="1" f=" 0.0000000E+00" rc=" 2.3114501247" e="-4.5017877E-02" id= "Ni3"/> <state l="1" rc=" 2.3114501247" e=" 2.0000000E+00" id= "Ni4"/> <state n=" 3" l="2" f=" 8.0000000E+00" rc=" 2.3114501247" e="-3.2611821E-01" id= "Ni5"/> <state l="2" rc=" 2.3114501247" e=" 5.0000000E-01" id= "Ni6"/> </valence_states> <radial_grid eq="r=a*(exp(d*i)-1)" a=" 6.0270380411551105E-04" d=" 1.6875706515234311E-02" istart="0" iend=" 699" id="log1"> <values> 0.0000000000000000E+00 1.0257359174222992E-05 2.0689287376400567E-05 3.1298755580348083E-05 4.2088785322604073E-05 5.3062449562951930E-05 6.4222873559588025E-05 7.5573235759182796E-05 8.7116768702090911E-05 9.8856759942966279E-05 1.1079655298704517E-04 1.2293954824236394E-04 1.3528920398818273E-04 1.4784903735988981E-04 1.6062262535066889E-04 1.7361360583021331E-04 1.8682567858077734E-04 2.0026260635086005E-04 2.1392821592682281E-04 2.2782639922274260E-04 2.4196111438881473E-04 2.5633638693861940E-04 2.7095631089557289E-04 2.8582504995888915E-04 3.0094683868938656E-04 3.1632598371547426E-04 3.3196686495966438E-04 3.4787393688595663E-04 3.6405172976845313E-04 3.8050485098156396E-04 3.9723798631216908E-04 4.1425590129411354E-04 4.3156344256541323E-04 4.4916553924855880E-04 4.6706720435431184E-04 4.8527353620939122E-04 5.0378971990845645E-04 5.2262102879080483E-04 5.4177282594219662E-04 5.6125056572224326E-04 5.8105979531778785E-04 6.0120615632272209E-04 6.2169538634469302E-04 6.4253332063914938E-04 6.6372589377120374E-04 6.8527914130577059E-04 7.0719920152647513E-04 7.2949231718381186E-04 7.5216483727305779E-04 7.7522321884244039E-04 7.9867402883208275E-04 8.2252394594424169E-04 8.4677976254537708E-04 8.7144838660059359E-04 8.9653684364100208E-04 9.2205227876456365E-04 9.4800195867098859E-04 9.7439327373126340E-04 1.0012337400924006E-03 1.0285310018180102E-03 1.0562928330652994E-03 1.0845271402991229E-03 1.1132419645437156E-03 1.1424454836727442E-03 1.1721460147383366E-03 1.2023520163397458E-03 1.2330720910323268E-03 1.2643149877775131E-03 1.2960896044344875E-03 1.3284049902942581E-03 1.3612703486568637E-03 1.3946950394524366E-03 1.4286885819068777E-03 1.4632606572528963E-03 1.4984211114871860E-03 1.5341799581745303E-03 1.5705473812996263E-03 1.6075337381674460E-03 1.6451495623529574E-03 1.6834055667010472E-03 1.7223126463774988E-03 1.7618818819718919E-03 1.8021245426533175E-03 1.8430520893797902E-03 1.8846761781622892E-03 1.9270086633843429E-03 1.9700616011781168E-03 2.0138472528579499E-03 2.0583780884123335E-03 2.1036667900553177E-03 2.1497262558383555E-03 2.1965696033236226E-03 2.2442101733198445E-03 2.2926615336817135E-03 2.3419374831739614E-03 2.3920520554011932E-03 2.4430195228046080E-03 2.4948544007267351E-03 2.5475714515453469E-03 2.6011856888777324E-03 2.6557123818565145E-03 2.7111670594782457E-03 2.7675655150260045E-03 2.8249238105672631E-03 2.8832582815283055E-03 2.9425855413464947E-03 3.0029224862017159E-03 3.0642862998283451E-03 3.1266944584091138E-03 3.1901647355522568E-03 3.2547152073533711E-03 3.3203642575434194E-03 3.3871305827243470E-03 3.4550331976938038E-03 3.5240914408604844E-03 3.5943249797516399E-03 3.6657538166143104E-03 3.7383982941118898E-03 3.8122791011176429E-03 3.8874172786068149E-03 3.9638342256490258E-03 4.0415517055026381E-03 4.1205918518128614E-03 4.2009771749153147E-03 4.2827305682469081E-03 4.3658753148657810E-03 4.4504350940822533E-03 4.5364339882025852E-03 4.6238964893875406E-03 4.7128475066276548E-03 4.8033123728372156E-03 4.8953168520690024E-03 4.9888871468517643E-03 5.0840499056526269E-03 5.1808322304664530E-03 5.2792616845344078E-03 5.3793663001938464E-03 5.4811745868618422E-03 5.5847155391545323E-03 5.6900186451447057E-03 5.7971138947598682E-03 5.9060317883232738E-03 6.0168033452403071E-03 6.1294601128326770E-03 6.2440341753229938E-03 6.3605581629722118E-03 6.4790652613726353E-03 6.5995892208990129E-03 6.7221643663205556E-03 6.8468256065764661E-03 6.9736084447179041E-03 7.1025489880190973E-03 7.2336839582605667E-03 7.3670507021873595E-03 7.5026872021452425E-03 7.6406320868979520E-03 7.7809246426284971E-03 7.9236048241277425E-03 8.0687132661733559E-03 8.2162912951024621E-03 8.3663809405812150E-03 8.5190249475746802E-03 8.6742667885204711E-03 8.8321506757094975E-03 8.9927215738774876E-03 9.1560252130107565E-03 9.3221081013699480E-03 9.4910175387353975E-03 9.6628016298779505E-03 9.8375092982589969E-03 1.0015190299963709E-02 1.0195895237871372E-02 1.0379675576066895E-02 1.0566583654497612E-02 1.0756672703879453E-02 1.0949996860856907E-02 1.1146611183420885E-02 1.1346571666589075E-02 1.1549935258353058E-02 1.1756759875896942E-02 1.1967104422091895E-02 1.2181028802271520E-02 1.2398593941292621E-02 1.2619861800886397E-02 1.2844895397304910E-02 1.3073758819267856E-02 1.3306517246214825E-02 1.3543236966868114E-02 1.3783985398111556E-02 1.4028831104190547E-02 1.4277843816238926E-02 1.4531094452138094E-02 1.4788655136714218E-02 1.5050599222279044E-02 1.5317001309520401E-02 1.5587937268748199E-02 1.5863484261501970E-02 1.6143720762526233E-02 1.6428726582119749E-02 1.6718582888865262E-02 1.7013372232745922E-02 1.7313178568655295E-02 1.7618087280307324E-02 1.7928185204553356E-02 1.8243560656112889E-02 1.8564303452725309E-02 1.8890504940729649E-02 1.9222258021079637E-02 1.9559657175801607E-02 1.9902798494902535E-02 2.0251779703736209E-02 2.0606700190834947E-02 2.0967661036215168E-02 2.1334765040164499E-02 2.1708116752519019E-02 2.2087822502438560E-02 2.2473990428688896E-02 2.2866730510439286E-02 2.3266154598584048E-02 2.3672376447597364E-02 2.4085511747930027E-02 2.4505678158957753E-02 2.4932995342490015E-02 2.5367584996849376E-02 2.5809570891530638E-02 2.6259078902449981E-02 2.6716237047793908E-02 2.7181175524478348E-02 2.7654026745228301E-02 2.8134925376288384E-02 2.8624008375775379E-02 2.9121415032683284E-02 2.9627287006552389E-02 3.0141768367813297E-02 3.0665005638817709E-02 3.1197147835567384E-02 3.1738346510153337E-02 3.2288755793917372E-02 3.2848532441347986E-02 3.3417835874723606E-02 3.3996828229515316E-02 3.4585674400562462E-02 3.5184542089034210E-02 3.5793601850189996E-02 3.6413027141953158E-02 3.7042994374311029E-02 3.7683682959555972E-02 3.8335275363381147E-02 3.8997957156846119E-02 3.9671917069226841E-02 4.0357347041764947E-02 4.1054442282332099E-02 4.1763401321024143E-02 4.2484426066701976E-02 4.3217721864494296E-02 4.3963497554279266E-02 4.4721965530161154E-02 4.5493341800959451E-02 4.6277846051727377E-02 4.7075701706317315E-02 4.7887135991011229E-02 4.8712379999233592E-02 4.9551668757366121E-02 5.0405241291682314E-02 5.1273340696421386E-02 5.2156214203020336E-02 5.3054113250524705E-02 5.3967293557197427E-02 5.4896015193346394E-02 5.5840542655391651E-02 5.6801144941192712E-02 5.7778095626658366E-02 5.8771672943659869E-02 5.9782159859270656E-02 6.0809844156353897E-02 6.1855018515522213E-02 6.2917980598491907E-02 6.3999033132856084E-02 6.5098483998300094E-02 6.6216646314284575E-02 6.7353838529220791E-02 6.8510384511163341E-02 6.9686613640046940E-02 7.0882860901492081E-02 7.2099466982208052E-02 7.3336778367019004E-02 7.4595147437541809E-02 7.5874932572542630E-02 7.7176498250002099E-02 7.8500215150917249E-02 7.9846460264869898E-02 8.1215616997392256E-02 8.2608075279158838E-02 8.4024231677037639E-02 8.5464489507030658E-02 8.6929258949137111E-02 8.8418957164170711E-02 8.9934008412565714E-02 9.1474844175204656E-02 9.3041903276302726E-02 9.4635632008382792E-02 9.6256484259378106E-02 9.7904921641897874E-02 9.9581413624692597E-02 1.0128643766635748E-01 1.0302047935131017E-01 1.0478403252808388E-01 1.0657759944997323E-01 1.0840169091807458E-01 1.1025682642675971E-01 1.1214353431162613E-01 1.1406235189996511E-01 1.1601382566379018E-01 1.1799851137547092E-01 1.2001697426601404E-01 1.2206978918603958E-01 1.2415754076949592E-01 1.2628082360016177E-01 1.2844024238098067E-01 1.3063641210627877E-01 1.3286995823691244E-01 1.3514151687839740E-01 1.3745173496206936E-01 1.3980127042932708E-01 1.4219079241901203E-01 1.4462098145797633E-01 1.4709252965489480E-01 1.4960614089737412E-01 1.5216253105241781E-01 1.5476242817030228E-01 1.5740657269192329E-01 1.6009571765966993E-01 1.6283062893188885E-01 1.6561208540099753E-01 1.6844087921530995E-01 1.7131781600463797E-01 1.7424371510973061E-01 1.7721940981562009E-01 1.8024574758893780E-01 1.8332359031927012E-01 1.8645381456462065E-01 1.8963731180105098E-01 1.9287498867656977E-01 1.9616776726934235E-01 1.9951658535029596E-01 2.0292239665019207E-01 2.0638617113124638E-01 2.0990889526336970E-01 2.1349157230511176E-01 2.1713522258938428E-01 2.2084088381404884E-01 2.2460961133744872E-01 2.2844247847897184E-01 2.3234057682472700E-01 2.3630501653842417E-01 2.4033692667754467E-01 2.4443745551489240E-01 2.4860777086561844E-01 2.5284906041980909E-01 2.5716253208073636E-01 2.6154941430886375E-01 2.6601095647170830E-01 2.7054842919965427E-01 2.7516312474782467E-01 2.7985635736411052E-01 2.8462946366346342E-01 2.8948380300855969E-01 2.9442075789693972E-01 2.9944173435473953E-01 3.0454816233712095E-01 3.0974149613551860E-01 3.1502321479181500E-01 3.2039482251956730E-01 3.2585784913240062E-01 3.3141385047969518E-01 3.3706440888968370E-01 3.4281113362009430E-01 3.4865566131646047E-01 3.5459965647823133E-01 3.6064481193281606E-01 3.6679284931769263E-01 3.7304551957072535E-01 3.7940460342882448E-01 3.8587191193509462E-01 3.9244928695461112E-01 3.9913860169897764E-01 4.0594176125980924E-01 4.1286070315129536E-01 4.1989739786199737E-01 4.2705384941603469E-01 4.3433209594382427E-01 4.4173421026253223E-01 4.4926230046640531E-01 4.5691851052714644E-01 4.6470502090451093E-01 4.7262404916729278E-01 4.8067785062487994E-01 4.8886871896955908E-01 4.9719898692974823E-01 5.0567102693435073E-01 5.1428725178841317E-01 5.2305011536028501E-01 5.3196211328046783E-01 5.4102578365236420E-01 5.5024370777511822E-01 5.5961851087876213E-01 5.6915286287186906E-01 5.7884947910193429E-01 5.8871112112869650E-01 5.9874059751061792E-01 6.0894076460475421E-01 6.1931452738023063E-01 6.2986484024556810E-01 6.4059470789008710E-01 6.5150718613963388E-01 6.6260538282686465E-01 6.7389245867634673E-01 6.8537162820472097E-01 6.9704616063618297E-01 7.0891938083354800E-01 7.2099467024515607E-01 7.3327546786789854E-01 7.4576527122662906E-01 7.5846763737024914E-01 7.7138618388473779E-01 7.8452458992342933E-01 7.9788659725482025E-01 8.1147601132821501E-01 8.2529670235749786E-01 8.3935260642335896E-01 8.5364772659427446E-01 8.6818613406656442E-01 8.8297196932385680E-01 8.9800944331627808E-01 9.1330283865971795E-01 9.2885651085550114E-01 9.4467488953082113E-01 9.6076247970027573E-01 9.7712386304888244E-01 9.9376369923692331E-01 1.0106867272269986E+00 1.0278977666336684E+00 1.0454017190960554E+00 1.0632035696738174E+00 1.0813083882668704E+00 1.0997213310592824E+00 1.1184476419877283E+00 1.1374926542349475E+00 1.1568617917486119E+00 1.1765605707860507E+00 1.1965946014852527E+00 1.2169695894626165E+00 1.2376913374378884E+00 1.2587657468867535E+00 1.2801988197215572E+00 1.3019966600006225E+00 1.3241654756666656E+00 1.3467115803147927E+00 1.3696413949905935E+00 1.3929614500188232E+00 1.4166783868632178E+00 1.4407989600179598E+00 1.4653300389313282E+00 1.4902786099620986E+00 1.5156517783692234E+00 1.5414567703353881E+00 1.5677009350249975E+00 1.5943917466771969E+00 1.6215368067344980E+00 1.6491438460076466E+00 1.6772207268773272E+00 1.7057754455333378E+00 1.7348161342518809E+00 1.7643510637115956E+00 1.7943886453490212E+00 1.8249374337541420E+00 1.8560061291067049E+00 1.8876035796539916E+00 1.9197387842307700E+00 1.9524208948221289E+00 1.9856592191699269E+00 2.0194632234236036E+00 2.0538425348360985E+00 2.0888069445056718E+00 2.1243664101643507E+00 2.1605310590138669E+00 2.1973111906098435E+00 2.2347172797950687E+00 2.2727599796826921E+00 2.3114501246901900E+00 2.3507987336249641E+00 2.3908170128224717E+00 2.4315163593377234E+00 2.4729083641911385E+00 2.5150048156696174E+00 2.5578177026838049E+00 2.6013592181824841E+00 2.6456417626250825E+00 2.6906779475132772E+00 2.7364805989826979E+00 2.7830627614557799E+00 2.8304377013567379E+00 2.8786189108898164E+00 2.9276201118818079E+00 2.9774552596899824E+00 3.0281385471765163E+00 3.0796844087505706E+00 3.1321075244791525E+00 3.1854228242679388E+00 3.2396454921132798E+00 3.2947909704265097E+00 3.3508749644319096E+00 3.4079134466394914E+00 3.4659226613939076E+00 3.5249191295007791E+00 3.5849196529317595E+00 3.6459413196096717E+00 3.7080015082750801E+00 3.7711178934357119E+00 3.8353084504000572E+00 3.9005914603966887E+00 3.9669855157806850E+00 4.0345095253286614E+00 4.1031827196239181E+00 4.1730246565332374E+00 4.2440552267768927E+00 4.3162946595934386E+00 4.3897635285009571E+00 4.4644827571562695E+00 4.5404736253139459E+00 4.6177577748866927E+00 4.6963572161088845E+00 4.7762943338049988E+00 4.8575918937647300E+00 4.9402730492265983E+00 5.0243613474718956E+00 5.1098807365309016E+00 5.1968555720031340E+00 5.2853106239937722E+00 5.3752710841680775E+00 5.4667625729258846E+00 5.5598111466981965E+00 5.6544433053679555E+00 5.7506859998171045E+00 5.8485666396021303E+00 5.9481131007601444E+00 6.0493537337479166E+00 6.1523173715159647E+00 6.2570333377200704E+00 6.3635314550725459E+00 6.4718420538356307E+00 6.5819959804594355E+00 6.6940246063668836E+00 6.8079598368882186E+00 6.9238341203474576E+00 7.0416804573035892E+00 7.1615324099490065E+00 7.2834241116678839E+00 7.4073902767572433E+00 7.5334662103134526E+00 7.6616878182869792E+00 7.7920916177082651E+00 7.9247147470876866E+00 8.0595949769923827E+00 8.1967707208032259E+00 8.3362810456547898E+00 8.4781656835615280E+00 8.6224650427333014E+00 8.7692202190834738E+00 8.9184730079328922E+00 9.0702659159129979E+00 9.2246421730716399E+00 9.3816457451847164E+00 9.5413213462775417E+00 9.7037144513591986E+00 9.8688713093736649E+00 1.0036838956371334E+01 1.0207665228904693E+01 1.0381398777652015E+01 1.0558089081272845E+01 1.0737786460499436E+01 1.0920542092467766E+01 1.1106408025292685E+01 1.1295437192891004E+01 1.1487683430056862E+01 1.1683201487793683E+01 1.1882047048907053E+01 1.2084276743862972E+01 1.2289948166915973E+01 1.2499119892511843E+01 1.2711851491969263E+01 1.2928203550445597E+01 1.3148237684191272E+01 1.3372016558097883E+01 1.3599603903544891E+01 1.3831064536550095E+01 1.4066464376228957E+01 1.4305870463568228E+01 1.4549350980518804E+01 1.4796975269413796E+01 1.5048813852716943E+01 1.5304938453107139E+01 1.5565422013904781E+01 1.5830338719845754E+01 1.6099764018208962E+01 1.6373774640303406E+01 1.6652448623321074E+01 1.6935865332561487E+01 1.7224105484034723E+01 1.7517251167449029E+01 1.7815385869589651E+01 1.8118594498095554E+01 1.8426963405640794E+01 1.8740580414527454E+01 1.9059534841697040E+01 1.9383917524167764E+01 1.9713820844904383E+01 2.0049338759128645E+01 2.0390566821077350E+01 2.0737602211215844E+01 2.1090543763914635E+01 2.1449491995597072E+01 2.1814549133366000E+01 2.2185819144117680E+01 2.2563407764151254E+01 2.2947422529281873E+01 2.3337972805466599E+01 2.3735169819951405E+01 2.4139126692948267E+01 2.4549958469851379E+01 2.4967782154001640E+01 2.5392716740008769E+01 2.5824883247640468E+01 2.6264404756288606E+01 2.6711406440021442E+01 2.7166015603232957E+01 2.7628361716898599E+01 2.8098576455448118E+01 2.8576793734265980E+01 2.9063149747829929E+01 2.9557783008498681E+01 3.0060834385959662E+01 3.0572447147348377E+01 3.1092766998050024E+01 3.1621942123196071E+01 3.2160123229866741E+01 3.2707463590011855E+01 3.3264119084102063E+01 3.3830248245523059E+01 3.4406012305725191E+01 3.4991575240141842E+01 3.5587103814888636E+01 3.6192767634258040E+01 3.6808739189021985E+01 3.7435193905556559E+01 3.8072310195802807E+01 3.8720269508077749E+01 3.9379256378750206E+01 4.0049458484795970E+01 4.0731066697247776E+01 4.1424275135554282E+01 4.2129281222864755E+01 4.2846285742254423E+01 4.3575492893906741E+01 4.4317110353268809E+01 4.5071349330196576E+01 4.5838424629106576E+01 4.6618554710151379E+01 4.7411961751436515E+01 4.8218871712295496E+01 4.9039514397642478E+01 4.9874123523419769E+01 5.0722936783159263E+01 5.1586195915676619E+01 5.2464146773917619E+01 5.3357039394976113E+01 5.4265128071303572E+01 5.5188671423130984E+01 5.6127932472122360E+01 5.7083178716282703E+01 5.8054682206140299E+01 5.9042719622225739E+01 6.0047572353869427E+01 6.1069526579340234E+01 6.2108873347348016E+01 6.3165908659933010E+01 6.4240933556766606E+01 6.5334254200885610E+01 6.6446181965886808E+01 6.7577033524604772E+01 6.8727130939299258E+01 6.9896801753377176E+01 7.1086379084675784E+01 7.2296201720333258E+01 7.3526614213274499E+01 7.4777966980337737E+01 7.6050616402072450E+01 7.7344924924235016E+01 7.8661261161012007E+01 8.0000000000000028E+01 </values> <derivatives> 1.0171052513868633E-05 1.0344152696914167E-05 1.0520198855642111E-05 1.0699241127334640E-05 1.0881330502555600E-05 1.1066518839672433E-05 1.1254858879625242E-05 1.1446404260947214E-05 1.1641209535040671E-05 1.1839330181713105E-05 1.2040822624977616E-05 1.2245744249122257E-05 1.2454153415052873E-05 1.2666109476914047E-05 1.2881672798992958E-05 1.3100904772910886E-05 1.3323867835107329E-05 1.3550625484621646E-05 1.3781242301177370E-05 1.4015783963574244E-05 1.4254317268393307E-05 1.4496910149020316E-05 1.4743631694992907E-05 1.4994552171677032E-05 1.5249743040278284E-05 1.5509276978193765E-05 1.5773227899710350E-05 1.6041670977055182E-05 1.6314682661804439E-05 1.6592340706656474E-05 1.6874724187575465E-05 1.7161913526311967E-05 1.7453990513306728E-05 1.7751038330984267E-05 1.8053141577442971E-05 1.8360386290548252E-05 1.8672859972435840E-05 1.8990651614432079E-05 1.9313851722398264E-05 1.9642552342506435E-05 1.9976847087453743E-05 2.0316831163122974E-05 2.0662601395696883E-05 2.1014256259233860E-05 2.1371895903713056E-05 2.1735622183556599E-05 2.2105538686637475E-05 2.2481750763780863E-05 2.2864365558767732E-05 2.3253492038848920E-05 2.3649241025778647E-05 2.4051725227376109E-05 2.4461059269624214E-05 2.4877359729314698E-05 2.5300745167248698E-05 2.5731336162002424E-05 2.6169255344267523E-05 2.6614627431775805E-05 2.7067579264818374E-05 2.7528239842369304E-05 2.7996740358824016E-05 2.8473214241362976E-05 2.8957797187951255E-05 2.9450627205984775E-05 2.9951844651594315E-05 3.0461592269618395E-05 3.0980015234256468E-05 3.1507261190413998E-05 3.2043480295751180E-05 3.2588825263447220E-05 3.3143451405692554E-05 3.3707516677921091E-05 3.4281181723795401E-05 3.4864609920957378E-05 3.5457967427557581E-05 3.6061423229576459E-05 3.6675149188950924E-05 3.7299320092519971E-05 3.7934113701803316E-05 3.8579710803627205E-05 3.9236295261611833E-05 3.9904054068534978E-05 4.0583177399586876E-05 4.1273858666531368E-05 4.1976294572788883E-05 4.2690685169456747E-05 4.3417233912283119E-05 4.4156147719610262E-05 4.4907637031304201E-05 4.5671915868687209E-05 4.6449201895490230E-05 4.7239716479842740E-05 4.8043684757317459E-05 4.8861335695048214E-05 4.9692902156938900E-05 5.0538620969982177E-05 5.1398732991706975E-05 5.2273483178773792E-05 5.3163120656737374E-05 5.4067898790996831E-05 5.4988075258953044E-05 5.5923912123394318E-05 5.6875675907130782E-05 5.7843637668899131E-05 5.8828073080559142E-05 5.9829262505603957E-05 6.0847491079006549E-05 6.1883048788425072E-05 6.2936230556790329E-05 6.4007336326298597E-05 6.5096671143834113E-05 6.6204545247845251E-05 6.7331274156699292E-05 6.8477178758540781E-05 6.9642585402679370E-05 7.0827825992532813E-05 7.2033238080151791E-05 7.3259164962353481E-05 7.4505955778491243E-05 7.5773965609888090E-05 7.7063555580962642E-05 7.8375092962075843E-05 7.9708951274128347E-05 8.1065510394937628E-05 8.2445156667426117E-05 8.3848283009649733E-05 8.5275289026699939E-05 8.6726581124509363E-05 8.8202572625595006E-05 8.9703683886770719E-05 9.1230342418863208E-05 9.2782983008465812E-05 9.4362047841763661E-05 9.5967986630467048E-05 9.7601256739887260E-05 9.9262323319192802E-05 1.0095165943388181E-04 1.0266974620050975E-04 1.0441707292370906E-04 1.0619413723554184E-04 1.0800144523722309E-04 1.0983951164325664E-04 1.1170885992802407E-04 1.1361002247486786E-04 1.1554354072771257E-04 1.1750996534526556E-04 1.1950985635784310E-04 1.2154378332686423E-04 1.2361232550706035E-04 1.2571607201144420E-04 1.2785562197908758E-04 1.3003158474575338E-04 1.3224458001743239E-04 1.3449523804683335E-04 1.3678419981287619E-04 1.3911211720324073E-04 1.4147965320002157E-04 1.4388748206854319E-04 1.4633628954938786E-04 1.4882677305369223E-04 1.5135964186176721E-04 1.5393561732509830E-04 1.5655543307178417E-04 1.5921983521547054E-04 1.6192958256784111E-04 1.6468544685472388E-04 1.6748821293587602E-04 1.7033867902850871E-04 1.7323765693461670E-04 1.7618597227217611E-04 1.7918446471027768E-04 1.8223398820826103E-04 1.8533541125891919E-04 1.8848961713584237E-04 1.9169750414497019E-04 1.9495998588042680E-04 1.9827799148470810E-04 2.0165246591329894E-04 2.0508437020379185E-04 2.0857468174958799E-04 2.1212439457825416E-04 2.1573451963461892E-04 2.1940608506868518E-04 2.2314013652844380E-04 2.2693773745767031E-04 2.3079996939878922E-04 2.3472793230089388E-04 2.3872274483300703E-04 2.4278554470267443E-04 2.4691748897997883E-04 2.5111975442706981E-04 2.5539353783330060E-04 2.5974005635607010E-04 2.6416054786746352E-04 2.6865627130679456E-04 2.7322850703914633E-04 2.7787855722001434E-04 2.8260774616615598E-04 2.8741742073274995E-04 2.9230895069697700E-04 2.9728372914812547E-04 3.0234317288433982E-04 3.0748872281611764E-04 3.1272184437667705E-04 3.1804402793930524E-04 3.2345678924181195E-04 3.2896166981820590E-04 3.3456023743771724E-04 3.4025408655129333E-04 3.4604483874569095E-04 3.5193414320529976E-04 3.5792367718182207E-04 3.6401514647194951E-04 3.7021028590316583E-04 3.7651085982782091E-04 3.8291866262561003E-04 3.8943551921460739E-04 3.9606328557099610E-04 4.0280384925764216E-04 4.0965912996166669E-04 4.1663108004116390E-04 4.2372168508122710E-04 4.3093296445943411E-04 4.3826697192095976E-04 4.4572579616347402E-04 4.5331156143199559E-04 4.6102642812386851E-04 4.6887259340403528E-04 4.7685229183078176E-04 4.8496779599212963E-04 4.9322141715306270E-04 5.0161550591376429E-04 5.1015245287906166E-04 5.1883468933925888E-04 5.2766468796256155E-04 5.3664496349928109E-04 5.4577807349802745E-04 5.5506661903408961E-04 5.6451324545021050E-04 5.7412064310997273E-04 5.8389154816400205E-04 5.9382874332921309E-04 6.0393505868131913E-04 6.1421337246082288E-04 6.2466661189273143E-04 6.3529775402021719E-04 6.4610982655247161E-04 6.5710590872698120E-04 6.6828913218648525E-04 6.7966268187085528E-04 6.9122979692415353E-04 7.0299377161713147E-04 7.1495795628542108E-04 7.2712575828370158E-04 7.3950064295609942E-04 7.5208613462310694E-04 7.6488581758529350E-04 7.7790333714410152E-04 7.9114240064001476E-04 8.0460677850839471E-04 8.1830030535328833E-04 8.3222688103950452E-04 8.4639047180328462E-04 8.6079511138186936E-04 8.7544490216229557E-04 8.9034401634973520E-04 9.0549669715572745E-04 9.2090726000662788E-04 9.3658009377262617E-04 9.5251966201768100E-04 9.6873050427072295E-04 9.8521723731849822E-04 1.0019845565204097E-03 1.0190372371457416E-03 1.0363801357336333E-03 1.0540181914762059E-03 1.0719564276252243E-03 1.0901999529227045E-03 1.1087539630558580E-03 1.1276237421368068E-03 1.1468146642074797E-03 1.1663321947701156E-03 1.1861818923438248E-03 1.2063694100476259E-03 1.2269004972104381E-03 1.2477810010084658E-03 1.2690168681304568E-03 1.2906141464712902E-03 1.3125789868543983E-03 1.3349176447834980E-03 1.3576364822241310E-03 1.3807419694155355E-03 1.4042406867133357E-03 1.4281393264636098E-03 1.4524446949088403E-03 1.4771637141263122E-03 1.5023034239994876E-03 1.5278709842229412E-03 1.5538736763414131E-03 1.5803189058235711E-03 1.6072142041710508E-03 1.6345672310634045E-03 1.6623857765395492E-03 1.6906777632163361E-03 1.7194512485448914E-03 1.7487144271053354E-03 1.7784756329405776E-03 1.8087433419298146E-03 1.8395261742024359E-03 1.8708328965929960E-03 1.9026724251379802E-03 1.9350538276150585E-03 1.9679863261255499E-03 2.0014792997208532E-03 2.0355422870735503E-03 2.0701849891939955E-03 2.1054172721931205E-03 2.1412491700922732E-03 2.1776908876808580E-03 2.2147528034226318E-03 2.2524454724114425E-03 2.2907796293772870E-03 2.3297661917435221E-03 2.3694162627360973E-03 2.4097411345457192E-03 2.4507522915438204E-03 2.4924614135532729E-03 2.5348803791747474E-03 2.5780212691696989E-03 2.6218963699009210E-03 2.6665181768316614E-03 2.7118993980842733E-03 2.7580529580594456E-03 2.8049920011170236E-03 2.8527298953194705E-03 2.9012802362390505E-03 2.9506568508297806E-03 3.0008738013653081E-03 3.0519453894437853E-03 3.1038861600609208E-03 3.1567109057523274E-03 3.2104346708063851E-03 3.2650727555488010E-03 3.3206407207000770E-03 3.3771543918071603E-03 3.4346298637504759E-03 3.4930835053277065E-03 3.5525319639155531E-03 3.6129921702108599E-03 3.6744813430523932E-03 3.7370169943247160E-03 3.8006169339454983E-03 3.8652992749377275E-03 3.9310824385882116E-03 3.9979851596939047E-03 4.0660264918974997E-03 4.1352258131138351E-03 4.2056028310486640E-03 4.2771775888113149E-03 4.3499704706229042E-03 4.4240022076216792E-03 4.4992938837671876E-03 4.5758669418448829E-03 4.6537431895729651E-03 4.7329448058131308E-03 4.8134943468870258E-03 4.8954147530002254E-03 4.9787293547754784E-03 5.0634618798972089E-03 5.1496364598690577E-03 5.2372776368864631E-03 5.3264103708261590E-03 5.4170600463546714E-03 5.5092524801577617E-03 5.6030139282929508E-03 5.6983710936671060E-03 5.7953511336413539E-03 5.8939816677653885E-03 5.9942907856434056E-03 6.0963070549339459E-03 6.2000595294858111E-03 6.3055777576125271E-03 6.4128917905075722E-03 6.5220321908028654E-03 6.6330300412728600E-03 6.7459169536868181E-03 6.8607250778117230E-03 6.9774871105684026E-03 7.0962363053435114E-03 7.2170064814599377E-03 7.3398320338084379E-03 7.4647479426431674E-03 7.5917897835439396E-03 7.7209937375479912E-03 7.8523966014542208E-03 7.9860357983027735E-03 8.1219493880329806E-03 8.2601760783227087E-03 8.4007552356121194E-03 8.5437268963151156E-03 8.6891317782215420E-03 8.8370112920934888E-03 8.9874075534588718E-03 9.1403633946058205E-03 9.2959223767811166E-03 9.4541288025963184E-03 9.6150277286449308E-03 9.7786649783343678E-03 9.9450871549363086E-03 1.0114341654859088E-02 1.0286476681146083E-02 1.0461541257203685E-02 1.0639585240763021E-02 1.0820659338079233E-02 1.1004815118372461E-02 1.1192105028514513E-02 1.1382582407965563E-02 1.1576301503965027E-02 1.1773317486980964E-02 1.1973686466422448E-02 1.2177465506619262E-02 1.2384712643073652E-02 1.2595486898988576E-02 1.2809848302077357E-02 1.3027857901659270E-02 1.3249577786046211E-02 1.3475071100225174E-02 1.3704402063841778E-02 1.3937635989489687E-02 1.4174839301311448E-02 1.4416079553915825E-02 1.4661425451617079E-02 1.4910946868001750E-02 1.5164714865828320E-02 1.5422801717265662E-02 1.5685280924475860E-02 1.5952227240547401E-02 1.6223716690784484E-02 1.6499826594358814E-02 1.6780635586329765E-02 1.7066223640039371E-02 1.7356672089888461E-02 1.7652063654500318E-02 1.7952482460278682E-02 1.8258014065366604E-02 1.8568745484013147E-02 1.8884765211354626E-02 1.9206163248617739E-02 1.9533031128751557E-02 1.9865461942495822E-02 2.0203550364892749E-02 2.0547392682250167E-02 2.0897086819563510E-02 2.1252732368404435E-02 2.1614430615284227E-02 2.1982284570499683E-02 2.2356398997470158E-02 2.2736880442573708E-02 2.3123837265491234E-02 2.3517379670066754E-02 2.3917619735693105E-02 2.4324671449231772E-02 2.4738650737475828E-02 2.5159675500165585E-02 2.5587865643565841E-02 2.6023343114614815E-02 2.6466231935654137E-02 2.6916658239750049E-02 2.7374750306615472E-02 2.7840638599143680E-02 2.8314455800563604E-02 2.8796336852227527E-02 2.9286418992041933E-02 2.9784841793552227E-02 3.0291747205692814E-02 3.0807279593213624E-02 3.1331585777794699E-02 3.1864815079860338E-02 3.2407119361105068E-02 3.2958653067743274E-02 3.3519573274494875E-02 3.4090039729319663E-02 3.4670214898912768E-02 3.5260264014974910E-02 3.5860355121269331E-02 3.6470659121480273E-02 3.7091349827885665E-02 3.7722604010858210E-02 3.8364601449208877E-02 3.9017524981387268E-02 3.9681560557553244E-02 4.0356897292535089E-02 4.1043727519688301E-02 4.1742246845671689E-02 4.2452654206155301E-02 4.3175151922476618E-02 4.3909945759260847E-02 4.4657244983021961E-02 4.5417262421760966E-02 4.6190214525578477E-02 4.6976321428319166E-02 4.7775807010264598E-02 4.8588898961893841E-02 4.9415828848728700E-02 5.0256832177282773E-02 5.1112148462132766E-02 5.1982021294131403E-02 5.2866698409781115E-02 5.3766431761788407E-02 5.4681477590819413E-02 5.5612096498475698E-02 5.6558553521512990E-02 5.7521118207322551E-02 5.8500064690697282E-02 5.9495671771904221E-02 6.0508222996085888E-02 6.1538006734012787E-02 6.2585316264210294E-02 6.3650449856483604E-02 6.4733710856863330E-02 6.5835407773997587E-02 6.6955854367014123E-02 6.8095369734877634E-02 6.9254278407268055E-02 7.0432910437005239E-02 7.1631601494046904E-02 7.2850692961085914E-02 7.4090532030775424E-02 7.5351471804607162E-02 7.6633871393473968E-02 7.7938096019943115E-02 7.9264517122270228E-02 8.0613512460183598E-02 8.1985466222468689E-02 8.3380769136383648E-02 8.4799818578936773E-02 8.6243018690058695E-02 8.7710780487698883E-02 8.9203521984882683E-02 9.0721668308759690E-02 9.2265651821678299E-02 9.3835912244320960E-02 9.5432896780934903E-02 9.7057060246694110E-02 9.8708865197229573E-02 1.0038878206036239E-01 1.0209728927008059E-01 1.0383487340279506E-01 1.0560202931591474E-01 1.0739926028878011E-01 1.0922707816599522E-01 1.1108600350319921E-01 1.1297656571531828E-01 1.1489930322734189E-01 1.1685476362766307E-01 1.1884350382403017E-01 1.2086609020215199E-01 1.2292309878700225E-01 1.2501511540686935E-01 1.2714273586019814E-01 1.2930656608527080E-01 1.3150722233277590E-01 1.3374533134131497E-01 1.3602153051589397E-01 1.3833646810945471E-01 1.4069080340749471E-01 1.4308520691582910E-01 1.4552036055154835E-01 1.4799695783722530E-01 1.5051570409842832E-01 1.5307731666459456E-01 1.5568252507332414E-01 1.5833207127814786E-01 1.6102670985983400E-01 1.6376720824128965E-01 1.6655434690612000E-01 1.6938891962090713E-01 1.7227173366127155E-01 1.7520361004178150E-01 1.7818538374977427E-01 1.8121790398315898E-01 1.8430203439226270E-01 1.8743865332579629E-01 1.9062865408100454E-01 1.9387294515807368E-01 1.9717245051886892E-01 2.0052810985007524E-01 2.0394087883081671E-01 2.0741172940482974E-01 2.1094165005727075E-01 2.1453164609623057E-01 2.1818273993904397E-01 2.2189597140346981E-01 2.2567239800382741E-01 2.2951309525217237E-01 2.3341915696459853E-01 2.3739169557275222E-01 2.4143184244065030E-01 2.4554074818688576E-01 2.4971958301232125E-01 2.5396953703335756E-01 2.5829182062087419E-01 2.6268766474493838E-01 2.6715832132538087E-01 2.7170506358833779E-01 2.7632918642886040E-01 2.8103200677969797E-01 2.8581486398635270E-01 2.9067912018852166E-01 2.9562616070802927E-01 3.0065739444336120E-01 3.0577425427091354E-01 3.1097819745307048E-01 3.1627070605322732E-01 3.2165328735787596E-01 3.2712747430587635E-01 3.3269482592502875E-01 3.3835692777608095E-01 3.4411539240428946E-01 3.4997185979866652E-01 3.5592799785904244E-01 3.6198550287107756E-01 3.6814609998935749E-01 3.7441154372871072E-01 3.8078361846388964E-01 3.8726413893775058E-01 3.9385495077808774E-01 4.0055793102326059E-01 4.0737498865676741E-01 4.1430806515091656E-01 4.2135913501975031E-01 4.2853020638137923E-01 4.3582332152988551E-01 4.4324055751696451E-01 4.5078402674345547E-01 4.5845587756094924E-01 4.6625829488362980E-01 4.7419350081052908E-01 4.8226375525837328E-01 4.9047135660519781E-01 4.9881864234491707E-01 5.0730798975303293E-01 5.1594181656367755E-01 5.2472258165816899E-01 5.3365278576529607E-01 5.4273497217351430E-01 5.5197172745526590E-01 5.6136568220362493E-01 5.7091951178148137E-01 5.8063593708347228E-01 5.9051772531088709E-01 6.0056769075974981E-01 6.1078869562232374E-01 6.2118365080225268E-01 6.3175551674357444E-01 6.4250730427384495E-01 6.5344207546160993E-01 6.6456294448847097E-01 6.7587307853599121E-01 6.8737569868770143E-01 6.9907408084644584E-01 7.1097155666735112E-01 7.2307151450666773E-01 7.3537740038676225E-01 7.4789271897753018E-01 7.6062103459451380E-01 7.7356597221400458E-01 7.8673121850542260E-01 8.0012052288127100E-01 8.1373769856494627E-01 8.2758662367673574E-01 8.4167124233828960E-01 8.5599556579589264E-01 8.7056367356285136E-01 8.8537971458132458E-01 9.0044790840392597E-01 9.1577254639543582E-01 9.3135799295497101E-01 9.4720868675894054E-01 9.6332914202517039E-01 9.7972394979853306E-01 9.9639777925846140E-01 1.0133553790487118E+00 1.0306015786297607E+00 1.0481412896542173E+00 1.0659795073656406E+00 1.0841213120211746E+00 1.1025718703383738E+00 1.1213364369666745E+00 1.1404203559838941E+00 1.1598290624182079E+00 1.1795680837960221E+00 1.1996430417161932E+00 1.2200596534510360E+00 1.2408237335745900E+00 1.2619411956185758E+00 1.2834180537565534E+00 1.3052604245167354E+00 1.3274745285239520E+00 1.3500666922712592E+00 </derivatives> </radial_grid> <shape_function type="sinc" rc=" 2.3114501246901900"/> <ae_core_density grid="log1" rc=" 2.3114501246901900"> 7.9847811016405583E+04 7.6376384231345219E+04 7.4103933528903668E+04 7.2776338315517452E+04 7.1827787146685499E+04 7.0380777726969100E+04 6.9731643299209885E+04 6.9230599511085296E+04 6.8765474356692997E+04 6.8353409193642670E+04 6.7979093450778382E+04 6.7634242544895431E+04 6.7313886418133465E+04 6.7013920461775997E+04 6.6731141099874978E+04 6.6463042683346925E+04 6.6207602187482684E+04 6.5963165883470341E+04 6.5728364949690571E+04 6.5502052792309449E+04 6.5283259056514362E+04 6.5071154977028033E+04 6.4865026809480609E+04 6.4664255220930339E+04 6.4468299095351285E+04 6.4276682664038693E+04 6.4088985173800029E+04 6.3904832514688154E+04 6.3723890377295560E+04 6.3545858615972953E+04 6.3370466571565688E+04 6.3197469164116723E+04 6.3026643608307859E+04 6.2857786636258978E+04 6.2690712136507966E+04 6.2525249136560531E+04 6.2361240070762979E+04 6.2198539286456071E+04 6.2037011750176389E+04 6.1876531922638482E+04 6.1716982776791723E+04 6.1558254937697420E+04 6.1400245926566422E+04 6.1242859494216245E+04 6.1086005031581692E+04 6.0929597046867864E+04 6.0773554700535846E+04 6.0617801390646229E+04 6.0462264382187524E+04 6.0306874474940530E+04 6.0151565705202702E+04 5.9996275077347811E+04 5.9840942321744078E+04 5.9685509676020185E+04 5.9529921687064969E+04 5.9374125031482901E+04 5.9218068352515918E+04 5.9061702111692146E+04 5.8904978453672578E+04 5.8747851082952286E+04 5.8590275151231966E+04 5.8432207154413540E+04 5.8273604838292689E+04 5.8114427112128134E+04 5.7954633969356553E+04 5.7794186414803808E+04 5.7633046397812752E+04 5.7471176750770275E+04 5.7308541132569619E+04 5.7145103976594102E+04 5.6980830442848630E+04 5.6815686373905497E+04 5.6649638254362304E+04 5.6482653173541257E+04 5.6314698791185467E+04 5.6145743305930206E+04 5.5975755426350603E+04 5.5804704344404061E+04 5.5632559711104310E+04 5.5459291614278191E+04 5.5284870558270908E+04 5.5109267445477657E+04 5.4932453559589529E+04 5.4754400550454331E+04 5.4575080420459082E+04 5.4394465512351788E+04 5.4212528498425258E+04 5.4029242370994922E+04 5.3844580434106945E+04 5.3658516296418908E+04 5.3471023865201714E+04 5.3282077341413897E+04 5.3091651215806116E+04 5.2899720266015065E+04 5.2706259554611606E+04 5.2511244428070488E+04 5.2314650516630994E+04 5.2116453735022049E+04 5.1916630284027218E+04 5.1715156652866346E+04 5.1512009622374550E+04 5.1307166268959219E+04 5.1100603969318588E+04 5.0892300405906979E+04 5.0682233573131678E+04 5.0470381784270678E+04 5.0256723679098264E+04 5.0041238232209165E+04 4.9823904762031219E+04 4.9604702940518357E+04 4.9383612803515905E+04 4.9160614761790792E+04 4.8935689612720722E+04 4.8708818552635130E+04 4.8479983189803213E+04 4.8249165558062748E+04 4.8016348131085004E+04 4.7781513837270832E+04 4.7544646075272438E+04 4.7305728730136907E+04 4.7064746190065853E+04 4.6821683363786608E+04 4.6576525698529986E+04 4.6329259198609288E+04 4.6079870444594351E+04 4.5828346613076428E+04 4.5574675497015392E+04 4.5318845526664918E+04 4.5060845791066153E+04 4.4800666060104180E+04 4.4538296807117418E+04 4.4273729232051322E+04 4.4006955285147029E+04 4.3737967691153113E+04 4.3466759974050532E+04 4.3193326482276672E+04 4.2917662414436454E+04 4.2639763845484515E+04 4.2359627753364744E+04 4.2077252046088011E+04 4.1792635589232552E+04 4.1505778233845180E+04 4.1216680844724491E+04 4.0925345329063064E+04 4.0631774665424593E+04 4.0335972933031830E+04 4.0037945341336992E+04 3.9737698259847733E+04 3.9435239248176505E+04 3.9130577086283178E+04 3.8823721804874986E+04 3.8514684715929288E+04 3.8203478443300563E+04 3.7890116953371602E+04 3.7574615585707375E+04 3.7256991083666442E+04 3.6937261624924511E+04 3.6615446851860375E+04 3.6291567901754242E+04 3.5965647436744293E+04 3.5637709673486344E+04 3.5307780412458145E+04 3.4975887066847754E+04 3.4642058690963335E+04 3.4306326008098309E+04 3.3968721437784305E+04 3.3629279122361106E+04 3.3288034952790804E+04 3.2945026593640192E+04 3.2600293507154234E+04 3.2253876976339052E+04 3.1905820126972489E+04 3.1556167948456259E+04 3.1204967313422458E+04 3.0852266996004513E+04 3.0498117688680024E+04 3.0142572017591938E+04 2.9785684556250944E+04 2.9427511837521924E+04 2.9068112363793258E+04 2.8707546615228544E+04 2.8345877055996527E+04 2.7983168138375571E+04 2.7619486304626473E+04 2.7254899986527031E+04 2.6889479602461452E+04 2.6523297551956010E+04 2.6156428207553512E+04 2.5788947903917615E+04 2.5420934924060195E+04 2.5052469482583176E+04 2.4683633705829809E+04 2.4314511608839162E+04 2.3945189069001313E+04 2.3575753796310975E+04 2.3206295300121055E+04 2.2836904852299904E+04 2.2467675446698828E+04 2.2098701754841448E+04 2.1730080077749033E+04 2.1361908293822362E+04 2.0994285802704286E+04 2.0627313465054183E+04 2.0261093538170953E+04 1.9895729607408593E+04 1.9531326513335174E+04 1.9167990274594762E+04 1.8805828006440002E+04 1.8444947834911974E+04 1.8085458806654649E+04 1.7727470794360281E+04 1.7371094397854744E+04 1.7016440840841609E+04 1.6663621863337710E+04 1.6312749609844130E+04 1.5963936513311437E+04 1.5617295174970601E+04 1.5272938240116444E+04 1.4930978269945328E+04 1.4591527609563700E+04 1.4254698252301321E+04 1.3920601700478132E+04 1.3589348822791797E+04 1.3261049708509174E+04 1.2935813518663301E+04 1.2613748334474873E+04 1.2294961003235274E+04 1.1979556981906564E+04 1.1667640178711799E+04 1.1359312793007753E+04 1.1054675153749718E+04 1.0753825556876795E+04 1.0456860101963208E+04 1.0163872528499402E+04 9.8749540521829749E+03 9.5901932016168812E+03 9.3096756558275429E+03 9.0334840830312442E+03 8.7616979810914072E+03 8.4943935201226213E+03 8.2316433877100208E+03 7.9735166372234935E+03 7.7200785397161681E+03 7.4713904399054873E+03 7.2275096167414176E+03 6.9884891490723603E+03 6.7543777869224086E+03 6.5252198288955879E+03 6.3010550062219700E+03 6.0819183739584641E+03 5.8678402098523475E+03 5.6588459213684273E+03 5.4549559613718366E+03 5.2561857529460149E+03 5.0625456238116658E+03 4.8740407507949985E+03 4.6906711147742699E+03 4.5124314665109287E+03 4.3393113037467483E+03 4.1712948599204292E+03 4.0083611048263683E+03 3.8504837575051411E+03 3.6976313116188276E+03 3.5497670735258885E+03 3.4068492132286515E+03 3.2688308283228757E+03 3.1356600210323263E+03 3.0072799883630310E+03 2.8836291253610661E+03 2.7646411414052354E+03 2.6502451894116402E+03 2.5403660077712047E+03 2.4349240747841714E+03 2.3338357752972647E+03 2.2370135791904522E+03 2.1443662313007408E+03 2.0557989523112701E+03 1.9712136500749054E+03 1.8905091407834459E+03 1.8135813793367197E+03 1.7403236982109586E+03 1.6706270540734604E+03 1.6043802813412599E+03 1.5414703518362805E+03 1.4817826396485380E+03 1.4252011902836427E+03 1.3716089931411825E+03 1.3208882563475170E+03 1.2729206829500060E+03 1.2275877474701244E+03 1.1847709718059170E+03 1.1443521994928437E+03 1.1062138673201596E+03 1.0702392733124734E+03 1.0363128401216070E+03 1.0043203728753124E+03 9.7414931055266084E+02 9.4568896997613444E+02 9.1883078153198107E+02 8.9346851575333915E+02 8.6949849992563134E+02 8.4681982390112194E+02 8.2533453433981094E+02 8.0494781662701166E+02 7.8556816375419100E+02 7.6710753148937943E+02 7.4948147920734903E+02 7.3260929579959418E+02 7.1641411014179687E+02 7.0082298566424379E+02 6.8576699865001945E+02 6.7118129997708422E+02 6.5700516012196499E+02 6.4318199735155304E+02 6.2965938914121318E+02 6.1638906696723063E+02 6.0332689472592631E+02 5.9043283112763368E+02 5.7767087650025371E+02 5.6500900451439531E+02 5.5241907941154352E+02 5.3987675937971142E+02 5.2736138677930637E+02 5.1485586597655913E+02 5.0234652959340895E+02 4.8982299403142650E+02 4.7727800517265615E+02 4.6470727520177616E+02 4.5210931153075990E+02 4.3948523883874776E+02 4.2683861526533241E+02 4.1417524381451585E+02 4.0150298003885371E+02 3.8883153707865182E+02 3.7617228912943307E+02 3.6353807440240297E+02 3.5094299862747420E+02 3.3840224012677328E+02 3.2593185745883989E+02 3.1354860060016892E+02 3.0126972659179211E+02 2.8911282053456421E+02 2.7709562276816393E+02 2.6523586301592485E+02 2.5355110222088692E+02 2.4205858273839488E+02 2.3077508748751148E+02 2.1971680859799750E+02 2.0889922602199266E+02 1.9833699651030585E+02 1.8804385328276854E+02 1.7803251665089056E+02 1.6831461577943847E+02 1.5890062170196543E+02 1.4979979163408095E+02 1.4102012455778123E+02 1.3256832798069627E+02 1.2444979570605301E+02 1.1666859638272382E+02 1.0922747254019934E+02 1.0212784975100087E+02 9.5369855503088743E+01 8.8952347307566924E+01 8.2872949512619655E+01 7.7128098243486804E+01 7.1713093840677871E+01 6.6622160124925273E+01 6.1848509778008271E+01 5.7384415094016312E+01 5.3221283326440116E+01 4.9349735833320032E+01 4.5759690206346647E+01 4.2440444561337479E+01 3.9380763166299005E+01 3.6568962598605744E+01 3.3992997641778310E+01 3.1640546167925919E+01 2.9499092304522062E+01 2.7556007246676792E+01 2.5798627160952940E+01 2.4214327703178512E+01 2.2790594761560730E+01 2.1515091135785976E+01 2.0375718933967224E+01 1.9360677539515184E+01 1.8458517045843191E+01 1.7658187066386997E+01 1.6949080787901018E+01 1.6321074049025274E+01 1.5764559124315140E+01 1.5270472831037589E+01 1.4830318606172687E+01 1.4436182344839201E+01 1.4080742018726777E+01 1.3757271336509568E+01 1.3459637898444978E+01 1.3182296397302066E+01 1.2920277432617684E+01 1.2669172467548075E+01 1.2425115402888348E+01 1.2184761194092729E+01 1.1945261902436057E+01 1.1704240549765663E+01 1.1459763133465318E+01 1.1210309150362828E+01 1.0954740972537351E+01 1.0692272412441753E+01 1.0422436808120951E+01 1.0145054950563555E+01 9.8602031635878831E+00 9.5681818316159184E+00 9.2694846520199707E+00 8.9647688665403500E+00 8.6548267009582371E+00 8.3405582143578272E+00 8.0229457296468709E+00 7.7030299862849754E+00 7.3818881251416748E+00 7.0606135847541918E+00 6.7402979585784610E+00 6.4220148346328747E+00 6.1068056126299641E+00 5.7956672695964686E+00 5.4895420233274841E+00 5.1893088239628709E+00 4.8957765875976236E+00 4.6096790721692109E+00 4.3316712848717449E+00 4.0623273019545252E+00 3.8021393758521480E+00 3.5515182010165809E+00 3.3107942084001665E+00 3.0802197590761451E+00 2.8599721097686284E+00 2.6501570268771193E+00 2.4508129306997568E+00 2.2619154577626901E+00 2.0833823362361361E+00 1.9150784771545266E+00 1.7568211923663493E+00 1.6083854586397788E+00 1.4695091559817983E+00 1.3398982168623699E+00 1.2192316314448868E+00 1.1071662622601948E+00 1.0033414295948673E+00 9.0738323627131523E-01 8.1890860773276553E-01 7.3752902958583189E-01 6.6285397087006181E-01 5.9449398669948517E-01 5.3206349877093806E-01 4.7518325652757532E-01 4.2348248551307893E-01 3.7660073267039407E-01 3.3418942104962895E-01 2.9591312861815139E-01 2.6145060764010969E-01 2.3049556244235089E-01 2.0275720434031269E-01 1.7796060309300651E-01 1.5584685452345684E-01 1.3617308391288982E-01 1.1871230448678896E-01 1.0325314979181267E-01 8.9599498047423273E-02 7.7570005677478279E-02 6.6997566216834531E-02 5.7728709677158610E-02 4.9622956274217631E-02 4.2552137193874469E-02 3.6399693831569976E-02 3.1059965703390501E-02 2.6437476015996546E-02 2.2446222714406383E-02 1.9008981713988311E-02 1.6056627975472835E-02 1.3527479105465937E-02 1.1366665263008894E-02 9.5255283261219195E-03 7.9610525203447462E-03 6.6353280325162347E-03 5.5150485255008180E-03 4.5710429312838929E-03 3.7778414288502787E-03 3.1132751074894644E-03 2.5581084733536383E-03 2.0957036744965606E-03 1.7117150939295880E-03 1.3938127874986962E-03 1.1314331190874236E-03 9.1555486481341799E-04 7.3849901527449802E-04 5.9375049520831369E-04 4.7580003796503706E-04 3.8000449302123682E-04 3.0246390381902222E-04 2.3991376636392045E-04 1.8963096258806591E-04 1.4935195327946867E-04 1.1720191064206897E-04 9.1633567956870386E-05 7.1374661421946399E-05 5.5382935469943505E-05 4.2807776420491476E-05 3.2957629223578308E-05 2.5272437533222551E-05 1.9300427874786693E-05 1.4678633872176303E-05 1.1116626176489393E-05 8.3829778098764321E-06 6.2940531406702168E-06 4.7047617601700576E-06 3.5009663303643089E-06 2.5932762624170522E-06 1.9119971552118624E-06 1.4030395866201829E-06 1.0246204392989152E-06 7.4461579710808157E-07 5.3844690692615324E-07 3.8740009632457362E-07 2.7729819111737842E-07 1.9745519344903628E-07 1.3985804741898818E-07 9.8529501347955549E-08 6.9034618058853914E-08 4.8100609229407564E-08 3.3325577240116838E-08 2.2956616848438567E-08 1.5721717869538658E-08 1.0703157983710000E-08 7.2427030917762038E-09 4.8710461767123959E-09 3.2556044032199113E-09 2.1621348467806612E-09 1.4266865724298625E-09 9.3523511604508524E-10 6.0898997939209121E-10 3.9386388058513887E-10 2.5297480495557084E-10 1.6134325406440269E-10 1.0216755493803882E-10 6.4225717544820801E-11 4.0075852613635196E-11 2.4818609121643100E-11 1.5252287304417097E-11 9.3002881631716439E-12 5.6260266171609156E-12 3.3759051517560216E-12 2.0090927332460075E-12 1.1856823292728784E-12 6.9379598086684537E-13 4.0246291008710683E-13 2.3141170389703103E-13 1.3186939405059864E-13 7.4462039301861738E-14 4.1657209876509770E-14 2.3085590235217516E-14 1.2671196865343307E-14 6.8873079744545775E-15 3.7065082234375615E-15 1.9746558845583250E-15 1.0412505212033237E-15 5.4335252358799517E-16 2.8054012767374464E-16 1.4329076385361515E-16 7.2389103627363011E-17 3.6164350690483551E-17 1.7863232424172970E-17 8.7222690450436556E-18 4.2092603664395591E-18 2.0072638200178554E-18 9.4566988807712169E-19 4.4007202042759461E-19 2.0224055189219353E-19 9.1766192862853902E-20 4.1103172836387542E-20 1.8169908987538408E-20 7.9253773105705358E-21 3.4102037488056411E-21 1.4472235859365029E-21 6.0560006543347875E-22 2.4982132653995226E-22 1.0156942984044509E-22 4.0689396229463574E-23 1.6057473726862963E-23 6.2408267291299048E-24 2.3881702840385601E-24 8.9956833933128709E-25 3.3345272954965448E-25 1.2160438519482160E-25 4.3617491221631422E-26 1.5383256178215517E-26 5.3332219426373802E-27 1.8170231384999247E-27 6.0818295380511876E-28 1.9993209287080600E-28 6.4531932304314834E-29 2.0444571440434467E-29 6.3556168143218266E-30 1.9381026517735709E-30 5.7955690990356245E-31 1.6989255055409558E-31 4.8805417328111695E-32 1.3735089334505017E-32 3.7854439979466335E-33 1.0213484895321257E-33 2.6968113201747579E-34 6.9661391591803120E-35 1.7597135390512969E-35 4.3455136458235064E-36 1.0486448768688498E-36 2.4719553052653334E-37 5.6899983152865707E-38 1.2784252615367631E-38 2.8025955104788721E-39 5.9923261551534713E-40 1.2491263984907377E-40 2.5375649622837718E-41 5.0216875013835821E-42 9.6766233224345417E-43 1.8149204461602848E-43 3.3118223316403025E-44 5.8771447075326052E-45 1.0138369455196585E-45 1.6993504955523007E-46 2.7664321939678613E-47 4.3720673482510298E-48 6.7048557334320458E-49 9.9731520628716084E-50 1.4381995958855980E-50 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 </ae_core_density> <pseudo_core_density grid="log1" rc=" 2.3114501246901900"> 3.8513162947641850E-02 3.8513162946348260E-02 3.8513162942378845E-02 3.8513162935597055E-02 3.8513162925860774E-02 3.8513162913022266E-02 3.8513162896927959E-02 3.8513162877418142E-02 3.8513162854326884E-02 3.8513162827481656E-02 3.8513162796703221E-02 3.8513162761805282E-02 3.8513162722594314E-02 3.8513162678869235E-02 3.8513162630421191E-02 3.8513162577033216E-02 3.8513162518479936E-02 3.8513162454527336E-02 3.8513162384932416E-02 3.8513162309442801E-02 3.8513162227796473E-02 3.8513162139721425E-02 3.8513162044935254E-02 3.8513161943144823E-02 3.8513161834045871E-02 3.8513161717322601E-02 3.8513161592647269E-02 3.8513161459679750E-02 3.8513161318067111E-02 3.8513161167443133E-02 3.8513161007427868E-02 3.8513160837627070E-02 3.8513160657631801E-02 3.8513160467017804E-02 3.8513160265345001E-02 3.8513160052156922E-02 3.8513159826980128E-02 3.8513159589323574E-02 3.8513159338678035E-02 3.8513159074515413E-02 3.8513158796288083E-02 3.8513158503428208E-02 3.8513158195346987E-02 3.8513157871433980E-02 3.8513157531056254E-02 3.8513157173557626E-02 3.8513156798257883E-02 3.8513156404451847E-02 3.8513155991408539E-02 3.8513155558370274E-02 3.8513155104551673E-02 3.8513154629138735E-02 3.8513154131287815E-02 3.8513153610124529E-02 3.8513153064742726E-02 3.8513152494203347E-02 3.8513151897533272E-02 3.8513151273724101E-02 3.8513150621730927E-02 3.8513149940471038E-02 3.8513149228822582E-02 3.8513148485623240E-02 3.8513147709668752E-02 3.8513146899711428E-02 3.8513146054458700E-02 3.8513145172571449E-02 3.8513144252662432E-02 3.8513143293294617E-02 3.8513142292979308E-02 3.8513141250174521E-02 3.8513140163282965E-02 3.8513139030650165E-02 3.8513137850562457E-02 3.8513136621244913E-02 3.8513135340859192E-02 3.8513134007501303E-02 3.8513132619199350E-02 3.8513131173911121E-02 3.8513129669521654E-02 3.8513128103840666E-02 3.8513126474599958E-02 3.8513124779450694E-02 3.8513123015960472E-02 3.8513121181610641E-02 3.8513119273793042E-02 3.8513117289807046E-02 3.8513115226856250E-02 3.8513113082045185E-02 3.8513110852375833E-02 3.8513108534744087E-02 3.8513106125935975E-02 3.8513103622623966E-02 3.8513101021362857E-02 3.8513098318585813E-02 3.8513095510600080E-02 3.8513092593582585E-02 3.8513089563575388E-02 3.8513086416481102E-02 3.8513083148057882E-02 3.8513079753914520E-02 3.8513076229505248E-02 3.8513072570124263E-02 3.8513068770900327E-02 3.8513064826790872E-02 3.8513060732576154E-02 3.8513056482853011E-02 3.8513052072028577E-02 3.8513047494313668E-02 3.8513042743715975E-02 3.8513037814032924E-02 3.8513032698844610E-02 3.8513027391505972E-02 3.8513021885139199E-02 3.8513016172625585E-02 3.8513010246597194E-02 3.8513004099428143E-02 3.8512997723225792E-02 3.8512991109821433E-02 3.8512984250760704E-02 3.8512977137293736E-02 3.8512969760364925E-02 3.8512962110602282E-02 3.8512954178306552E-02 3.8512945953439862E-02 3.8512937425613979E-02 3.8512928584078211E-02 3.8512919417706827E-02 3.8512909914986154E-02 3.8512900064001057E-02 3.8512889852421184E-02 3.8512879267486450E-02 3.8512868295992334E-02 3.8512856924274336E-02 3.8512845138192302E-02 3.8512832923113735E-02 3.8512820263896984E-02 3.8512807144873519E-02 3.8512793549829803E-02 3.8512779461988403E-02 3.8512764863988511E-02 3.8512749737865913E-02 3.8512734065031910E-02 3.8512717826252027E-02 3.8512701001623462E-02 3.8512683570552229E-02 3.8512665511729126E-02 3.8512646803105129E-02 3.8512627421865848E-02 3.8512607344405064E-02 3.8512586546297509E-02 3.8512565002270460E-02 3.8512542686174593E-02 3.8512519570953717E-02 3.8512495628613481E-02 3.8512470830189043E-02 3.8512445145711491E-02 3.8512418544173407E-02 3.8512390993492816E-02 3.8512362460476332E-02 3.8512332910780725E-02 3.8512302308873286E-02 3.8512270617990889E-02 3.8512237800097458E-02 3.8512203815840168E-02 3.8512168624504114E-02 3.8512132183965195E-02 3.8512094450641694E-02 3.8512055379444063E-02 3.8512014923722769E-02 3.8511973035214836E-02 3.8511929663987997E-02 3.8511884758383352E-02 3.8511838264955779E-02 3.8511790128412500E-02 3.8511740291549405E-02 3.8511688695185141E-02 3.8511635278093169E-02 3.8511579976931221E-02 3.8511522726168486E-02 3.8511463458010216E-02 3.8511402102319868E-02 3.8511338586538345E-02 3.8511272835600720E-02 3.8511204771849883E-02 3.8511134314947383E-02 3.8511061381781057E-02 3.8510985886369670E-02 3.8510907739764011E-02 3.8510826849944932E-02 3.8510743121717581E-02 3.8510656456602163E-02 3.8510566752720875E-02 3.8510473904681049E-02 3.8510377803454177E-02 3.8510278336250856E-02 3.8510175386391357E-02 3.8510068833171825E-02 3.8509958551725891E-02 3.8509844412881432E-02 3.8509726283012531E-02 3.8509604023886271E-02 3.8509477492504232E-02 3.8509346540938814E-02 3.8509211016163468E-02 3.8509070759877549E-02 3.8508925608324890E-02 3.8508775392106231E-02 3.8508619935985283E-02 3.8508459058687931E-02 3.8508292572694794E-02 3.8508120284026420E-02 3.8507941992021337E-02 3.8507757489106308E-02 3.8507566560558794E-02 3.8507368984261277E-02 3.8507164530447009E-02 3.8506952961437302E-02 3.8506734031369484E-02 3.8506507485915824E-02 3.8506273061992585E-02 3.8506030487459209E-02 3.8505779480807176E-02 3.8505519750838171E-02 3.8505250996331161E-02 3.8504972905698188E-02 3.8504685156628221E-02 3.8504387415718877E-02 3.8504079338095437E-02 3.8503760567016987E-02 3.8503430733468701E-02 3.8503089455740595E-02 3.8502736338991442E-02 3.8502370974797986E-02 3.8501992940688616E-02 3.8501601799661077E-02 3.8501197099683623E-02 3.8500778373179126E-02 3.8500345136491532E-02 3.8499896889333883E-02 3.8499433114217697E-02 3.8498953275862488E-02 3.8498456820585378E-02 3.8497943175669569E-02 3.8497411748711310E-02 3.8496861926944514E-02 3.8496293076542128E-02 3.8495704541893848E-02 3.8495095644858771E-02 3.8494465683992833E-02 3.8493813933749517E-02 3.8493139643653425E-02 3.8492442037445458E-02 3.8491720312198843E-02 3.8490973637404925E-02 3.8490201154027653E-02 3.8489401973525794E-02 3.8488575176841698E-02 3.8487719813355588E-02 3.8486834899804034E-02 3.8485919419161567E-02 3.8484972319483980E-02 3.8483992512712319E-02 3.8482978873435852E-02 3.8481930237613038E-02 3.8480845401248596E-02 3.8479723119025755E-02 3.8478562102891495E-02 3.8477361020593931E-02 3.8476118494169563E-02 3.8474833098379090E-02 3.8473503359089944E-02 3.8472127751603691E-02 3.8470704698926501E-02 3.8469232569980777E-02 3.8467709677755854E-02 3.8466134277395932E-02 3.8464504564222797E-02 3.8462818671691504E-02 3.8461074669276493E-02 3.8459270560285912E-02 3.8457404279601815E-02 3.8455473691343424E-02 3.8453476586451492E-02 3.8451410680190298E-02 3.8449273609565349E-02 3.8447062930653315E-02 3.8444776115841711E-02 3.8442410550975074E-02 3.8439963532404517E-02 3.8437432263937622E-02 3.8434813853685225E-02 3.8432105310801622E-02 3.8429303542114802E-02 3.8426405348642965E-02 3.8423407421993537E-02 3.8420306340640933E-02 3.8417098566078930E-02 3.8413780438843567E-02 3.8410348174402240E-02 3.8406797858904933E-02 3.8403125444792435E-02 3.8399326746257401E-02 3.8395397434553377E-02 3.8391333033146513E-02 3.8387128912705133E-02 3.8382780285921750E-02 3.8378282202162321E-02 3.8373629541936738E-02 3.8368817011185087E-02 3.8363839135373744E-02 3.8358690253395049E-02 3.8353364511264282E-02 3.8347855855607557E-02 3.8342158026933915E-02 3.8336264552684678E-02 3.8330168740053044E-02 3.8323863668566820E-02 3.8317342182426432E-02 3.8310596882591044E-02 3.8303620118604366E-02 3.8296403980152452E-02 3.8288940288344939E-02 3.8281220586711212E-02 3.8273236131902685E-02 3.8264977884092291E-02 3.8256436497061716E-02 3.8247602307967053E-02 3.8238465326773184E-02 3.8229015225346608E-02 3.8219241326196883E-02 3.8209132590855961E-02 3.8198677607884771E-02 3.8187864580495987E-02 3.8176681313782136E-02 3.8165115201536932E-02 3.8153153212658782E-02 3.8140781877124115E-02 3.8127987271518449E-02 3.8114755004112814E-02 3.8101070199472745E-02 3.8086917482587017E-02 3.8072280962502973E-02 3.8057144215455092E-02 3.8041490267473395E-02 3.8025301576457643E-02 3.8008560013703618E-02 3.7991246844867384E-02 3.7973342710353283E-02 3.7954827605111013E-02 3.7935680857827780E-02 3.7915881109500310E-02 3.7895406291372641E-02 3.7874233602224548E-02 3.7852339484996056E-02 3.7829699602733365E-02 3.7806288813841342E-02 3.7782081146628350E-02 3.7757049773128722E-02 3.7731166982188841E-02 3.7704404151802838E-02 3.7676731720684351E-02 3.7648119159060800E-02 3.7618534938677811E-02 3.7587946502001236E-02 3.7556320230605122E-02 3.7523621412734708E-02 3.7489814210034410E-02 3.7454861623431472E-02 3.7418725458167074E-02 3.7381366287968051E-02 3.7342743418353357E-02 3.7302814849071254E-02 3.7261537235664416E-02 3.7218865850162389E-02 3.7174754540902480E-02 3.7129155691482764E-02 3.7082020178852794E-02 3.7033297330551031E-02 3.6982934881100230E-02 3.6930878927575690E-02 3.6877073884365147E-02 3.6821462437141801E-02 3.6763985496077976E-02 3.6704582148329841E-02 3.6643189609829964E-02 3.6579743176429362E-02 3.6514176174436641E-02 3.6446419910609144E-02 3.6376403621656832E-02 3.6304054423328916E-02 3.6229297259159993E-02 3.6152054848963167E-02 3.6072247637165669E-02 3.5989793741095330E-02 3.5904608899335291E-02 3.5816606420279257E-02 3.5725697131031214E-02 3.5631789326809271E-02 3.5534788721028436E-02 3.5434598396254527E-02 3.5331118756239566E-02 3.5224247479268916E-02 3.5113879473071888E-02 3.4999906831570463E-02 3.4882218793765664E-02 3.4760701705088215E-02 3.4635238981568547E-02 3.4505711077212502E-02 3.4371995455002712E-02 3.4233966561981619E-02 3.4091495808910528E-02 3.3944451555041576E-02 3.3792699098583664E-02 3.3636100673492118E-02 3.3474515453263673E-02 3.3307799562474399E-02 3.3135806096857699E-02 3.2958385152784597E-02 3.2775383867077651E-02 3.2586646468164018E-02 3.2392014339653705E-02 3.2191326097514454E-02 3.1984417682107295E-02 3.1771122466445714E-02 3.1551271382147958E-02 3.1324693064665579E-02 3.1091214019494818E-02 3.0850658811207771E-02 3.0602850277282507E-02 3.0347609768861774E-02 3.0084757420733049E-02 2.9814112452996380E-02 2.9535493507073907E-02 2.9248719018914779E-02 2.8953607632464830E-02 2.8649978656700169E-02 2.8337652569771589E-02 2.8016451574071535E-02 2.7686200206319220E-02 2.7346726007064323E-02 2.6997860254336252E-02 2.6639438766515356E-02 2.6271302779878269E-02 2.5893299906670803E-02 2.5505285179992891E-02 2.5107122192241666E-02 2.4698684334353290E-02 2.4279856143613825E-02 2.3850534768377694E-02 2.3410631558639951E-02 2.2960073792061029E-02 2.2498806545739679E-02 2.2026794724778528E-02 2.1544025259487187E-02 2.1050509483925776E-02 2.0546285709411020E-02 2.0031422007590713E-02 1.9506019218746853E-02 1.8970214202116205E-02 1.8424183346226451E-02 1.7868146358539803E-02 1.7302370355082863E-02 1.6727174272225722E-02 1.6142933624362261E-02 1.5550085632946469E-02 1.4949134754160395E-02 1.4340658634441504E-02 1.3725314525185169E-02 1.3103846190175121E-02 1.2477091341687731E-02 1.1845989643780190E-02 1.1211591324015857E-02 1.0575066437817563E-02 9.9377148327846679E-03 9.3009768636746620E-03 8.6664449123542830E-03 8.0358757708817036E-03 7.4112039500099777E-03 6.7945559798208320E-03 6.1882657739284778E-03 5.5948911337556769E-03 5.0172314748035919E-03 4.4583468626369360E-03 3.9215784525134020E-03 3.4105704332319992E-03 2.9292935828836224E-03 2.4820705518003418E-03 2.0736029961435491E-03 1.7090006942893775E-03 1.3938127874986936E-03 1.1314331190874236E-03 9.1555486481341799E-04 7.3849901527449802E-04 5.9375049520831369E-04 4.7580003796503706E-04 3.8000449302123682E-04 3.0246390381902222E-04 2.3991376636392045E-04 1.8963096258806591E-04 1.4935195327946867E-04 1.1720191064206897E-04 9.1633567956870386E-05 7.1374661421946399E-05 5.5382935469943505E-05 4.2807776420491476E-05 3.2957629223578308E-05 2.5272437533222551E-05 1.9300427874786693E-05 1.4678633872176303E-05 1.1116626176489393E-05 8.3829778098764321E-06 6.2940531406702168E-06 4.7047617601700576E-06 3.5009663303643089E-06 2.5932762624170522E-06 1.9119971552118624E-06 1.4030395866201829E-06 1.0246204392989152E-06 7.4461579710808157E-07 5.3844690692615324E-07 3.8740009632457362E-07 2.7729819111737842E-07 1.9745519344903628E-07 1.3985804741898818E-07 9.8529501347955549E-08 6.9034618058853914E-08 4.8100609229407564E-08 3.3325577240116838E-08 2.2956616848438567E-08 1.5721717869538658E-08 1.0703157983710000E-08 7.2427030917762038E-09 4.8710461767123959E-09 3.2556044032199113E-09 2.1621348467806612E-09 1.4266865724298625E-09 9.3523511604508524E-10 6.0898997939209121E-10 3.9386388058513887E-10 2.5297480495557084E-10 1.6134325406440269E-10 1.0216755493803882E-10 6.4225717544820801E-11 4.0075852613635196E-11 2.4818609121643100E-11 1.5252287304417097E-11 9.3002881631716439E-12 5.6260266171609156E-12 3.3759051517560216E-12 2.0090927332460075E-12 1.1856823292728784E-12 6.9379598086684537E-13 4.0246291008710683E-13 2.3141170389703103E-13 1.3186939405059864E-13 7.4462039301861738E-14 4.1657209876509770E-14 2.3085590235217516E-14 1.2671196865343307E-14 6.8873079744545775E-15 3.7065082234375615E-15 1.9746558845583250E-15 1.0412505212033237E-15 5.4335252358799517E-16 2.8054012767374464E-16 1.4329076385361515E-16 7.2389103627363011E-17 3.6164350690483551E-17 1.7863232424172970E-17 8.7222690450436556E-18 4.2092603664395591E-18 2.0072638200178554E-18 9.4566988807712169E-19 4.4007202042759461E-19 2.0224055189219353E-19 9.1766192862853902E-20 4.1103172836387542E-20 1.8169908987538408E-20 7.9253773105705358E-21 3.4102037488056411E-21 1.4472235859365029E-21 6.0560006543347875E-22 2.4982132653995226E-22 1.0156942984044509E-22 4.0689396229463574E-23 1.6057473726862963E-23 6.2408267291299048E-24 2.3881702840385601E-24 8.9956833933128709E-25 3.3345272954965448E-25 1.2160438519482160E-25 4.3617491221631422E-26 1.5383256178215517E-26 5.3332219426373802E-27 1.8170231384999247E-27 6.0818295380511876E-28 1.9993209287080600E-28 6.4531932304314834E-29 2.0444571440434467E-29 6.3556168143218266E-30 1.9381026517735709E-30 5.7955690990356245E-31 1.6989255055409558E-31 4.8805417328111695E-32 1.3735089334505017E-32 3.7854439979466335E-33 1.0213484895321257E-33 2.6968113201747579E-34 6.9661391591803120E-35 1.7597135390512969E-35 4.3455136458235064E-36 1.0486448768688498E-36 2.4719553052653334E-37 5.6899983152865707E-38 1.2784252615367631E-38 2.8025955104788721E-39 5.9923261551534713E-40 1.2491263984907377E-40 2.5375649622837718E-41 5.0216875013835821E-42 9.6766233224345417E-43 1.8149204461602848E-43 3.3118223316403025E-44 5.8771447075326052E-45 1.0138369455196585E-45 1.6993504955523007E-46 2.7664321939678613E-47 4.3720673482510298E-48 6.7048557334320458E-49 9.9731520628716084E-50 1.4381995958855980E-50 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 </pseudo_core_density> <pseudo_valence_density grid="log1" rc=" 2.3114501246901900"> 8.4634038290455418E-02 8.4634038290480565E-02 8.4634038290557587E-02 8.4634038290689231E-02 8.4634038290878247E-02 8.4634038291127436E-02 8.4634038291439825E-02 8.4634038291818564E-02 8.4634038292266775E-02 8.4634038292787872E-02 8.4634038293385339E-02 8.4634038294062755E-02 8.4634038294823882E-02 8.4634038295672717E-02 8.4634038296613201E-02 8.4634038297649677E-02 8.4634038298786365E-02 8.4634038300027983E-02 8.4634038301379111E-02 8.4634038302844716E-02 8.4634038304429934E-02 8.4634038306140025E-02 8.4634038307980483E-02 8.4634038309956999E-02 8.4634038312075582E-02 8.4634038314342255E-02 8.4634038316763485E-02 8.4634038319345850E-02 8.4634038322096233E-02 8.4634038325021921E-02 8.4634038328130143E-02 8.4634038331428685E-02 8.4634038334925443E-02 8.4634038338628773E-02 8.4634038342547291E-02 8.4634038346689880E-02 8.4634038351065782E-02 8.4634038355684615E-02 8.4634038360556371E-02 8.4634038365691361E-02 8.4634038371100326E-02 8.4634038376794368E-02 8.4634038382785090E-02 8.4634038389084426E-02 8.4634038395704839E-02 8.4634038402659151E-02 8.4634038409960879E-02 8.4634038417623680E-02 8.4634038425662153E-02 8.4634038434091105E-02 8.4634038442926052E-02 8.4634038452183077E-02 8.4634038461878808E-02 8.4634038472030632E-02 8.4634038482656340E-02 8.4634038493774655E-02 8.4634038505404810E-02 8.4634038517566818E-02 8.4634038530281480E-02 8.4634038543570295E-02 8.4634038557455632E-02 8.4634038571960613E-02 8.4634038587109411E-02 8.4634038602926842E-02 8.4634038619438828E-02 8.4634038636672251E-02 8.4634038654654950E-02 8.4634038673415832E-02 8.4634038692984859E-02 8.4634038713393145E-02 8.4634038734672984E-02 8.4634038756857849E-02 8.4634038779982559E-02 8.4634038804083170E-02 8.4634038829197067E-02 8.4634038855363192E-02 8.4634038882621845E-02 8.4634038911014883E-02 8.4634038940585687E-02 8.4634038971379513E-02 8.4634039003443073E-02 8.4634039036825023E-02 8.4634039071575837E-02 8.4634039107747916E-02 8.4634039145395745E-02 8.4634039184575807E-02 8.4634039225346902E-02 8.4634039267769884E-02 8.4634039311908230E-02 8.4634039357827678E-02 8.4634039405596662E-02 8.4634039455286220E-02 8.4634039506970196E-02 8.4634039560725419E-02 8.4634039616631573E-02 8.4634039674771705E-02 8.4634039735231925E-02 8.4634039798101995E-02 8.4634039863475174E-02 8.4634039931448357E-02 8.4634040002122574E-02 8.4634040075602629E-02 8.4634040151997894E-02 8.4634040231422000E-02 8.4634040313993214E-02 8.4634040399834770E-02 8.4634040489074844E-02 8.4634040581846925E-02 8.4634040678290237E-02 8.4634040778549594E-02 8.4634040882775971E-02 8.4634040991126688E-02 8.4634041103765684E-02 8.4634041220863945E-02 8.4634041342599622E-02 8.4634041469158650E-02 8.4634041600734913E-02 8.4634041737530724E-02 8.4634041879757066E-02 8.4634042027634457E-02 8.4634042181392782E-02 8.4634042341272434E-02 8.4634042507524196E-02 8.4634042680410193E-02 8.4634042860204498E-02 8.4634043047193269E-02 8.4634043241675921E-02 8.4634043443965495E-02 8.4634043654389438E-02 8.4634043873290321E-02 8.4634044101026762E-02 8.4634044337974085E-02 8.4634044584525267E-02 8.4634044841092021E-02 8.4634045108105696E-02 8.4634045386018181E-02 8.4634045675303249E-02 8.4634045976457739E-02 8.4634046290002707E-02 8.4634046616484854E-02 8.4634046956477887E-02 8.4634047310583979E-02 8.4634047679435581E-02 8.4634048063697023E-02 8.4634048464066039E-02 8.4634048881276222E-02 8.4634049316098567E-02 8.4634049769344119E-02 8.4634050241865766E-02 8.4634050734561081E-02 8.4634051248374753E-02 8.4634051784301362E-02 8.4634052343388319E-02 8.4634052926739242E-02 8.4634053535516882E-02 8.4634054170947007E-02 8.4634054834322042E-02 8.4634055527005120E-02 8.4634056250434325E-02 8.4634057006127375E-02 8.4634057795686390E-02 8.4634058620803018E-02 8.4634059483264149E-02 8.4634060384957591E-02 8.4634061327878443E-02 8.4634062314135727E-02 8.4634063345959479E-02 8.4634064425708588E-02 8.4634065555878463E-02 8.4634066739109975E-02 8.4634067978198654E-02 8.4634069276104257E-02 8.4634070635961525E-02 8.4634072061091151E-02 8.4634073555011860E-02 8.4634075121452962E-02 8.4634076764368016E-02 8.4634078487949294E-02 8.4634080296643141E-02 8.4634082195166688E-02 8.4634084188525222E-02 8.4634086282031090E-02 8.4634088481323783E-02 8.4634090792391287E-02 8.4634093221593057E-02 8.4634095775684370E-02 8.4634098461842361E-02 8.4634101287694136E-02 8.4634104261346113E-02 8.4634107391416302E-02 8.4634110687067762E-02 8.4634114158045337E-02 8.4634117814713958E-02 8.4634121668100415E-02 8.4634125729937268E-02 8.4634130012710557E-02 8.4634134529709651E-02 8.4634139295081706E-02 8.4634144323889215E-02 8.4634149632171474E-02 8.4634155237010608E-02 8.4634161156601773E-02 8.4634167410328504E-02 8.4634174018843072E-02 8.4634181004152334E-02 8.4634188389709611E-02 8.4634196200512990E-02 8.4634204463210044E-02 8.4634213206210090E-02 8.4634222459804134E-02 8.4634232256293143E-02 8.4634242630124826E-02 8.4634253618040431E-02 8.4634265259231095E-02 8.4634277595505888E-02 8.4634290671469936E-02 8.4634304534716681E-02 8.4634319236032138E-02 8.4634334829613869E-02 8.4634351373304911E-02 8.4634368928843934E-02 8.4634387562132901E-02 8.4634407343522913E-02 8.4634428348120280E-02 8.4634450656113316E-02 8.4634474353122449E-02 8.4634499530573656E-02 8.4634526286098799E-02 8.4634554723963112E-02 8.4634584955522257E-02 8.4634617099711429E-02 8.4634651283568452E-02 8.4634687642792389E-02 8.4634726322341911E-02 8.4634767477074574E-02 8.4634811272430360E-02 8.4634857885162978E-02 8.4634907504121809E-02 8.4634960331087764E-02 8.4635016581667638E-02 8.4635076486250113E-02 8.4635140291028074E-02 8.4635208259091987E-02 8.4635280671599145E-02 8.4635357829023775E-02 8.4635440052494001E-02 8.4635527685221174E-02 8.4635621094028904E-02 8.4635720670987596E-02 8.4635826835162062E-02 8.4635940034481050E-02 8.4636060747735192E-02 8.4636189486714627E-02 8.4636326798493214E-02 8.4636473267872353E-02 8.4636629519992818E-02 8.4636796223127975E-02 8.4636974091670300E-02 8.4637163889324032E-02 8.4637366432519373E-02 8.4637582594061622E-02 8.4637813307033904E-02 8.4638059568968249E-02 8.4638322446305855E-02 8.4638603079164612E-02 8.4638902686436090E-02 8.4639222571233894E-02 8.4639564126718164E-02 8.4639928842321382E-02 8.4640318310403473E-02 8.4640734233364781E-02 8.4641178431249520E-02 8.4641652849871976E-02 8.4642159569501746E-02 8.4642700814146293E-02 8.4643278961470864E-02 8.4643896553399919E-02 8.4644556307446023E-02 8.4645261128815874E-02 8.4646014123346006E-02 8.4646818611324295E-02 8.4647678142258098E-02 8.4648596510651916E-02 8.4649577772864179E-02 8.4650626265114354E-02 8.4651746622719751E-02 8.4652943800643365E-02 8.4654223095441961E-02 8.4655590168707703E-02 8.4657051072103751E-02 8.4658612274101083E-02 8.4660280688529418E-02 8.4662063705063489E-02 8.4663969221774424E-02 8.4666005679882583E-02 8.4668182100858649E-02 8.4670508126028179E-02 8.4672994058845291E-02 8.4675650910012001E-02 8.4678490445630236E-02 8.4681525238585381E-02 8.4684768723374271E-02 8.4688235254601618E-02 8.4691940169385402E-02 8.4695899853924297E-02 8.4700131814497856E-02 8.4704654753186379E-02 8.4709488648613870E-02 8.4714654842038328E-02 8.4720176129130784E-02 8.4726076857807392E-02 8.4732383032499234E-02 8.4739122425267863E-02 8.4746324694199487E-02 8.4754021509535191E-02 8.4762246688021792E-02 8.4771036335995781E-02 8.4780429001742930E-02 8.4790465837705373E-02 8.4801190773142604E-02 8.4812650697883976E-02 8.4824895657847801E-02 8.4837979063037167E-02 8.4851957908762002E-02 8.4866893010876243E-02 8.4882849255860010E-02 8.4899895866620195E-02 8.4918106684926456E-02 8.4937560471446003E-02 8.4958341224386433E-02 8.4980538517806362E-02 8.5004247860700460E-02 8.5029571078018007E-02 8.5056616714825714E-02 8.5085500464875244E-02 8.5116345624892467E-02 8.5149283575954221E-02 8.5184454293374415E-02 8.5222006886572069E-02 8.5262100170445485E-02 8.5304903269826940E-02 8.5350596258641637E-02 8.5399370835437957E-02 8.5451431037002229E-02 8.5506993991805863E-02 8.5566290715069368E-02 8.5629566947254668E-02 8.5697084037817312E-02 8.5769119876063546E-02 8.5845969870959382E-02 8.5927947981731367E-02 8.6015387801075704E-02 8.6108643692758086E-02 8.6208091985331345E-02 8.6314132223626855E-02 8.6427188479579628E-02 8.6547710723828622E-02 8.6676176259385673E-02 8.6813091218488167E-02 8.6958992123536513E-02 8.7114447512765314E-02 8.7280059631000884E-02 8.7456466185512269E-02 8.7644342166567968E-02 8.7844401731851665E-02 8.8057400153370186E-02 8.8284135824895471E-02 8.8525452327310392E-02 8.8782240548475541E-02 8.9055440853382059E-02 8.9346045299412008E-02 8.9655099890462608E-02 8.9983706862518595E-02 9.0333026991949450E-02 9.0704281916364343E-02 9.1098756456270302E-02 9.1517800924027309E-02 9.1962833404679936E-02 9.2435341991147779E-02 9.2936886953975104E-02 9.3469102823354244E-02 9.4033700358448366E-02 9.4632468376126988E-02 9.5267275408095514E-02 9.5940071152030210E-02 9.6652887678728650E-02 9.7407840353435887E-02 9.8207128425424561E-02 9.9053035235575487E-02 9.9947927987149146E-02 1.0089425702015181E-01 1.0189455452470898E-01 1.0295143262367480E-01 1.0406758074936573E-01 1.0524576223383604E-01 1.0648881002656424E-01 1.0779962144783282E-01 1.0918115188054761E-01 1.1063640729780332E-01 1.1216843551827899E-01 1.1378031607662958E-01 1.1547514859155583E-01 1.1725603951033145E-01 1.1912608710539468E-01 1.2108836459637394E-01 1.2314590126979107E-01 1.2530166146893570E-01 1.2755852132826301E-01 1.2991924313041869E-01 1.3238644716996717E-01 1.3496258101640018E-01 1.3764988608041856E-01 1.4045036140217371E-01 1.4336572459856181E-01 1.4639736992917912E-01 1.4954632346762903E-01 1.5281319539698171E-01 1.5619812948572484E-01 1.5970074984402158E-01 1.6332010510984030E-01 1.6705461027099466E-01 1.7090198639260795E-01 1.7485919859026114E-01 1.7892239266725668E-01 1.8308683092003949E-01 1.8734682770877456E-01 1.9169568549002045E-01 1.9612563211487535E-01 2.0062776030807578E-01 2.0519197036019160E-01 2.0980691718485367E-01 2.1445996301398143E-01 2.1913713712401345E-01 2.2382310410236086E-01 2.2850114227247736E-01 2.3315313399419213E-01 2.3775956963893241E-01 2.4229956710215764E-01 2.4675090875226866E-01 2.5109009772031760E-01 2.5529243540155433E-01 2.5933212196129224E-01 2.6318238150659679E-01 2.6681561339474663E-01 2.7020357089219282E-01 2.7331756806729801E-01 2.7612871539064199E-01 2.7860818402353194E-01 2.8072749819553666E-01 2.8245885440459012E-01 2.8377546542034660E-01 2.8465192623824809E-01 2.8506459822732072E-01 2.8499200675272524E-01 2.8441524655334882E-01 2.8331838813955651E-01 2.8168887747692095E-01 2.7951792027460376E-01 2.7680084134434835E-01 2.7353740878549609E-01 2.6973211223541044E-01 2.6539438415881872E-01 2.6053875319088005E-01 2.5518491895311868E-01 2.4935773858042343E-01 2.4308711647473069E-01 2.3640779056826897E-01 2.2935901065077047E-01 2.2198410708344427E-01 2.1432995145346256E-01 2.0644631435079608E-01 1.9838512937404171E-01 1.9019967655624492E-01 1.8194370247148228E-01 1.7367049812998134E-01 1.6543195915787412E-01 1.5727765543383282E-01 1.4925393906261397E-01 1.4140312006517233E-01 1.3376273825664936E-01 1.2636495733389308E-01 1.1923610316494680E-01 1.1239636274837822E-01 1.0585965352078648E-01 9.9633665028146412E-02 9.3720066996424198E-02 8.8114870242964174E-02 8.2808920475505782E-02 7.7789304082764646E-02 7.3042254791647943E-02 6.8551824544012860E-02 6.4303049642797025E-02 6.0282436981049486E-02 5.6477537067400461E-02 5.2876850934198513E-02 4.9469742763958054E-02 4.6246358256516573E-02 4.3197548706668282E-02 4.0314800714760179E-02 3.7590171411391274E-02 3.5016229042185577E-02 3.2585998729600975E-02 3.0292913205664025E-02 2.8130768292068991E-02 2.6093682891792879E-02 2.4176063248765284E-02 2.2372571228606874E-02 2.0678096373375945E-02 1.9087731485924658E-02 1.7596751504104724E-02 1.6200595430876583E-02 1.4894851092572794E-02 1.3675242503419349E-02 1.2537619619315985E-02 1.1477950267409026E-02 1.0492314039995395E-02 9.5768979418895898E-03 8.7279935799699088E-03 7.9419956828751821E-03 7.2154017389331384E-03 6.5448125373115118E-03 5.9269334156309217E-03 5.3585759967153986E-03 4.8366602323918388E-03 4.3582165724959845E-03 3.9203880962770639E-03 3.5204324626865974E-03 3.1557235576332734E-03 2.8237527393355820E-03 2.5221296065347271E-03 2.2485822376777697E-03 2.0009568714523607E-03 1.7772170195828876E-03 1.5754420210656209E-03 1.3938250626705660E-03 1.2306707033696751E-03 1.0843919503042776E-03 9.5350694103819216E-04 8.3663529131043103E-04 7.3249416952943117E-04 6.3989415911599719E-04 5.5773496781707480E-04 4.8500103960924903E-04 4.2075712013166981E-04 3.6414382107460499E-04 3.1437322293400167E-04 2.7072454933627245E-04 2.3253994002306943E-04 1.9922034380398415E-04 1.7022154752740912E-04 1.4505035252113623E-04 1.2326090609055234E-04 1.0445119255216545E-04 8.8259685891231693E-05 7.4362164391087295E-05 6.2468686386406953E-05 5.2320725525850546E-05 4.3688463471495556E-05 3.6368237701184976E-05 3.0180141919355427E-05 2.4965776446508273E-05 2.0586145794113201E-05 1.6919700408919989E-05 1.3860519276083410E-05 1.1316629707291771E-05 9.2084602226123717E-06 7.4674219844569192E-06 6.0346137836940769E-06 4.8596451364482272E-06 3.8995716483245080E-06 3.1179364597257929E-06 2.4839113159375144E-06 1.9715306181078374E-06 1.5590117106186341E-06 1.2281546466796626E-06 9.6381474357011119E-07 7.5344138509519109E-07 5.8667674262332937E-07 4.5500835720049002E-07 3.5146984265057749E-07 2.7038432207882269E-07 2.0714558696459265E-07 1.5803235895166528E-07 1.2005143039994849E-07 9.0805852795345639E-08 6.8384725513426012E-08 5.1271505750188701E-08 3.8268109447123203E-08 2.8432399671617868E-08 2.1026961129750705E-08 1.5477336162331421E-08 1.1338148362443444E-08 8.2657651548081972E-09 5.9963511106051071E-09 4.3283406466973492E-09 3.1085135707863994E-09 2.2209913671330006E-09 1.5785879599030522E-09 1.1160477685608773E-09 7.8478798926821883E-10 5.4883294388308019E-10 3.8168768673520891E-10 2.6394738663210380E-10 1.8147971644620347E-10 1.2405085842347754E-10 8.4292906365574163E-11 5.6932418469001298E-11 3.8217521530128909E-11 2.5495043845544679E-11 1.6900306460246947E-11 1.1130977693435887E-11 7.2832534713750697E-12 4.7339480941396222E-12 3.0561818511456486E-12 1.9594911118977434E-12 1.2475721273346255E-12 7.8866981183445272E-13 4.9497122494075325E-13 3.0836630088843758E-13 1.9067869893995922E-13 1.1701212689287294E-13 7.1252010630894529E-14 4.3047116847431662E-14 2.5799651439865065E-14 1.5337251557678398E-14 9.0424319599326401E-15 5.2864726460505580E-15 3.0642748788731381E-15 1.7607890372179267E-15 1.0028606496591488E-15 5.6605964235565259E-16 3.1659618729587850E-16 1.7542983673660156E-16 9.6291238457264436E-17 5.2346263183361209E-17 2.8179226084886137E-17 1.5019122309524015E-17 7.9242574517860312E-18 4.1380552998884182E-18 2.1383637275809017E-18 1.0932941735683174E-18 5.5294753790569256E-19 2.7659364768408910E-19 1.3681396610207937E-19 6.6906116408578379E-20 3.2341798488703459E-20 1.5450404068883981E-20 7.2929926180257243E-21 3.4007399277527459E-21 1.5662199281413683E-21 7.1228237286025338E-22 3.1980016373058758E-22 1.4172208841939240E-22 6.1977283468750584E-23 2.6740270949909429E-23 1.1379884352999217E-23 4.7758152168547564E-24 1.9760228348858755E-24 8.0587303762641501E-25 3.2386590044059711E-25 1.2822706496133952E-25 5.0003478942972563E-26 1.9200614746388417E-26 7.2578996075658421E-27 2.7000533618685214E-27 9.8828471787912965E-28 3.5581235245261766E-28 1.2597028370779925E-28 4.3843005886097027E-29 1.4996595273588406E-29 5.0398564173035920E-30 1.6635957050916276E-30 5.3920076743041136E-31 1.7155097445018772E-31 5.3560012310895389E-32 1.6404222771925694E-32 4.9271838735132347E-33 1.4508699503165667E-33 4.1869825669962106E-34 1.1837799094917902E-34 3.2778566614641971E-35 8.8860345853894745E-36 2.3576144321483335E-36 6.1196956049929475E-37 1.5535400543601246E-37 3.8555988697951112E-38 9.3514074218794402E-39 2.2157190317242598E-39 5.1267200900965397E-40 1.1579350982483379E-40 2.5519930279813550E-41 5.4859718618050705E-42 1.1498081008457401E-42 2.3487162559506878E-43 4.6748544384935118E-44 9.0545679916960090E-45 1.6994612993403500E-45 3.1019807348265606E-46 5.5035762657315933E-47 9.4867892304338869E-48 </pseudo_valence_density> <zero_potential grid="log1" rc=" 2.3114501246901900"> -3.9384893365436304E+00 -3.9384893369378240E+00 -3.9384893381472739E+00 -3.9384893402136556E+00 -3.9384893431802896E+00 -3.9384893470921480E+00 -3.9384893519960524E+00 -3.9384893579406408E+00 -3.9384893649764914E+00 -3.9384893731561745E+00 -3.9384893825343030E+00 -3.9384893931676306E+00 -3.9384894051151309E+00 -3.9384894184380741E+00 -3.9384894332000955E+00 -3.9384894494673057E+00 -3.9384894673083801E+00 -3.9384894867946083E+00 -3.9384895080000466E+00 -3.9384895310015993E+00 -3.9384895558790776E+00 -3.9384895827153832E+00 -3.9384896115965633E+00 -3.9384896426119216E+00 -3.9384896758541714E+00 -3.9384897114195447E+00 -3.9384897494078999E+00 -3.9384897899228766E+00 -3.9384898330719946E+00 -3.9384898789668630E+00 -3.9384899277232375E+00 -3.9384899794612429E+00 -3.9384900343054947E+00 -3.9384900923852544E+00 -3.9384901538346124E+00 -3.9384902187926514E+00 -3.9384902874036301E+00 -3.9384903598171745E+00 -3.9384904361884381E+00 -3.9384905166783324E+00 -3.9384906014537209E+00 -3.9384906906876176E+00 -3.9384907845594288E+00 -3.9384908832551426E+00 -3.9384909869676306E+00 -3.9384910958968211E+00 -3.9384912102499694E+00 -3.9384913302419440E+00 -3.9384914560954760E+00 -3.9384915880414271E+00 -3.9384917263190911E+00 -3.9384918711765016E+00 -3.9384920228707072E+00 -3.9384921816681207E+00 -3.9384923478448521E+00 -3.9384925216870244E+00 -3.9384927034911343E+00 -3.9384928935644643E+00 -3.9384930922253596E+00 -3.9384932998037230E+00 -3.9384935166413841E+00 -3.9384937430924811E+00 -3.9384939795239600E+00 -3.9384942263159672E+00 -3.9384944838623528E+00 -3.9384947525711285E+00 -3.9384950328649642E+00 -3.9384953251817256E+00 -3.9384956299750029E+00 -3.9384959477146158E+00 -3.9384962788872535E+00 -3.9384966239970085E+00 -3.9384969835660146E+00 -3.9384973581350922E+00 -3.9384977482643460E+00 -3.9384981545338920E+00 -3.9384985775445602E+00 -3.9384990179185797E+00 -3.9384994763003434E+00 -3.9384999533572049E+00 -3.9385004497802454E+00 -3.9385009662851371E+00 -3.9385015036129705E+00 -3.9385020625311435E+00 -3.9385026438343314E+00 -3.9385032483453517E+00 -3.9385038769162226E+00 -3.9385045304291282E+00 -3.9385052097975120E+00 -3.9385059159671298E+00 -3.9385066499171999E+00 -3.9385074126615649E+00 -3.9385082052498812E+00 -3.9385090287688596E+00 -3.9385098843436221E+00 -3.9385107731389364E+00 -3.9385116963606732E+00 -3.9385126552572070E+00 -3.9385136511208763E+00 -3.9385146852895634E+00 -3.9385157591482129E+00 -3.9385168741305248E+00 -3.9385180317205983E+00 -3.9385192334546995E+00 -3.9385204809231222E+00 -3.9385217757719695E+00 -3.9385231197051764E+00 -3.9385245144864545E+00 -3.9385259619413993E+00 -3.9385274639596499E+00 -3.9385290224970664E+00 -3.9385306395780417E+00 -3.9385323172979190E+00 -3.9385340578253727E+00 -3.9385358634050234E+00 -3.9385377363600376E+00 -3.9385396790948168E+00 -3.9385416940978928E+00 -3.9385437839447639E+00 -3.9385459513009202E+00 -3.9385481989249969E+00 -3.9385505296719536E+00 -3.9385529464964533E+00 -3.9385554524562565E+00 -3.9385580507158284E+00 -3.9385607445500237E+00 -3.9385635373478967E+00 -3.9385664326166232E+00 -3.9385694339856552E+00 -3.9385725452108891E+00 -3.9385757701790229E+00 -3.9385791129121306E+00 -3.9385825775723200E+00 -3.9385861684665464E+00 -3.9385898900516190E+00 -3.9385937469394179E+00 -3.9385977439021982E+00 -3.9386018858781529E+00 -3.9386061779771318E+00 -3.9386106254865703E+00 -3.9386152338776119E+00 -3.9386200088114864E+00 -3.9386249561459716E+00 -3.9386300819422706E+00 -3.9386353924719941E+00 -3.9386408942244042E+00 -3.9386465939139241E+00 -3.9386524984879037E+00 -3.9386586151346612E+00 -3.9386649512917526E+00 -3.9386715146545987E+00 -3.9386783131853647E+00 -3.9386853551221046E+00 -3.9386926489883303E+00 -3.9387002036027816E+00 -3.9387080280896516E+00 -3.9387161318890600E+00 -3.9387245247679279E+00 -3.9387332168312463E+00 -3.9387422185337160E+00 -3.9387515406917575E+00 -3.9387611944959637E+00 -3.9387711915240011E+00 -3.9387815437538505E+00 -3.9387922635776560E+00 -3.9388033638159259E+00 -3.9388148577322455E+00 -3.9388267590485131E+00 -3.9388390819607317E+00 -3.9388518411552589E+00 -3.9388650518256418E+00 -3.9388787296900722E+00 -3.9388928910094010E+00 -3.9389075526057504E+00 -3.9389227318817923E+00 -3.9389384468406963E+00 -3.9389547161067133E+00 -3.9389715589464762E+00 -3.9389889952910910E+00 -3.9390070457588608E+00 -3.9390257316789046E+00 -3.9390450751154860E+00 -3.9390650988932663E+00 -3.9390858266233062E+00 -3.9391072827300340E+00 -3.9391294924791307E+00 -3.9391524820063144E+00 -3.9391762783471345E+00 -3.9392009094677811E+00 -3.9392264042969440E+00 -3.9392527927587238E+00 -3.9392801058067026E+00 -3.9393083754591292E+00 -3.9393376348353444E+00 -3.9393679181933967E+00 -3.9393992609689352E+00 -3.9394316998154744E+00 -3.9394652726459860E+00 -3.9395000186758131E+00 -3.9395359784672350E+00 -3.9395731939753227E+00 -3.9396117085954918E+00 -3.9396515672125862E+00 -3.9396928162516422E+00 -3.9397355037303563E+00 -3.9397796793133488E+00 -3.9398253943681749E+00 -3.9398727020232980E+00 -3.9399216572280151E+00 -3.9399723168142788E+00 -3.9400247395607626E+00 -3.9400789862589298E+00 -3.9401351197813828E+00 -3.9401932051524957E+00 -3.9402533096213421E+00 -3.9403155027371803E+00 -3.9403798564273451E+00 -3.9404464450777446E+00 -3.9405153456161028E+00 -3.9405866375978893E+00 -3.9406604032951593E+00 -3.9407367277882837E+00 -3.9408156990607348E+00 -3.9408974080970398E+00 -3.9409819489838931E+00 -3.9410694190146507E+00 -3.9411599187972497E+00 -3.9412535523656449E+00 -3.9413504272949478E+00 -3.9414506548202639E+00 -3.9415543499594694E+00 -3.9416616316399238E+00 -3.9417726228293972E+00 -3.9418874506711341E+00 -3.9420062466233303E+00 -3.9421291466031692E+00 -3.9422562911354322E+00 -3.9423878255058522E+00 -3.9425238999195220E+00 -3.9426646696641798E+00 -3.9428102952788326E+00 -3.9429609427276766E+00 -3.9431167835795642E+00 -3.9432779951930668E+00 -3.9434447609074263E+00 -3.9436172702394647E+00 -3.9437957190866522E+00 -3.9439803099364470E+00 -3.9441712520822003E+00 -3.9443687618456207E+00 -3.9445730628061648E+00 -3.9447843860374276E+00 -3.9450029703506009E+00 -3.9452290625454856E+00 -3.9454629176689084E+00 -3.9457047992810015E+00 -3.9459549797292852E+00 -3.9462137404309634E+00 -3.9464813721634586E+00 -3.9467581753634433E+00 -3.9470444604346069E+00 -3.9473405480642016E+00 -3.9476467695486974E+00 -3.9479634671286385E+00 -3.9482909943329925E+00 -3.9486297163330022E+00 -3.9489800103059154E+00 -3.9493422658086663E+00 -3.9497168851616506E+00 -3.9501042838428919E+00 -3.9505048908925939E+00 -3.9509191493284841E+00 -3.9513475165718006E+00 -3.9517904648843962E+00 -3.9522484818168238E+00 -3.9527220706677650E+00 -3.9532117509548601E+00 -3.9537180588969933E+00 -3.9542415479083681E+00 -3.9547827891042204E+00 -3.9553423718185985E+00 -3.9559209041340755E+00 -3.9565190134237094E+00 -3.9571373469051974E+00 -3.9577765722075418E+00 -3.9584373779502164E+00 -3.9591204743350716E+00 -3.9598265937510906E+00 -3.9605564913922717E+00 -3.9613109458887537E+00 -3.9620907599515518E+00 -3.9628967610311783E+00 -3.9637298019904881E+00 -3.9645907617923579E+00 -3.9654805462025440E+00 -3.9664000885086090E+00 -3.9673503502555953E+00 -3.9683323219995246E+00 -3.9693470240798252E+00 -3.9703955074122534E+00 -3.9714788543038884E+00 -3.9725981792923473E+00 -3.9737546300116868E+00 -3.9749493880877376E+00 -3.9761836700665554E+00 -3.9774587283798120E+00 -3.9787758523520558E+00 -3.9801363692553520E+00 -3.9815416454179728E+00 -3.9829930873945796E+00 -3.9844921432070581E+00 -3.9860403036661589E+00 -3.9876391037859884E+00 -3.9892901243052026E+00 -3.9909949933307614E+00 -3.9927553881226774E+00 -3.9945730370407158E+00 -3.9964497216771244E+00 -3.9983872792027206E+00 -4.0003876049578260E+00 -4.0024526553231832E+00 -4.0045844509113078E+00 -4.0067850801234606E+00 -4.0090567031233348E+00 -4.0114015562848246E+00 -4.0138219571779414E+00 -4.0163203101645655E+00 -4.0188991126832150E+00 -4.0215609623111259E+00 -4.0243085647002603E+00 -4.0271447424934834E+00 -4.0300724453369368E+00 -4.0330947611138583E+00 -4.0362149285351281E+00 -4.0394363512308704E+00 -4.0427626134955119E+00 -4.0461974978460367E+00 -4.0497450045583552E+00 -4.0534093733484022E+00 -4.0571951073643868E+00 -4.0611069996496454E+00 -4.0651501622239348E+00 -4.0693300579110030E+00 -4.0736525350100123E+00 -4.0781238648683722E+00 -4.0827507823564613E+00 -4.0875405291713696E+00 -4.0925008998048398E+00 -4.0976402898917010E+00 -4.1029677465101528E+00 -4.1084930198294085E+00 -4.1142266152872402E+00 -4.1201798452289262E+00 -4.1263648786460569E+00 -4.1327947873141495E+00 -4.1394835862447099E+00 -4.1464462659368087E+00 -4.1536988134420563E+00 -4.1612582187507838E+00 -4.1691424624754232E+00 -4.1773704802692126E+00 -4.1859620988948967E+00 -4.1949379383825409E+00 -4.2043192743181015E+00 -4.2141278540466276E+00 -4.2243856605013166E+00 -4.2351146175460928E+00 -4.2463362312266648E+00 -4.2580711622298653E+00 -4.2703387262285135E+00 -4.2831563207045367E+00 -4.2965387793647132E+00 -4.3104976583868462E+00 -4.3250404624816499E+00 -4.3401698230623573E+00 -4.3558826455421542E+00 -4.3721692477844769E+00 -4.3890125167254359E+00 -4.4063871148516478E+00 -4.4242587721581970E+00 -4.4425837019834535E+00 -4.4613081802709793E+00 -4.4803683268940402E+00 -4.4996901243432772E+00 -4.5191897030542529E+00 -4.5387739138931309E+00 -4.5583411969532737E+00 -4.5777827422183286E+00 -4.5969839225206401E+00 -4.6158259633844585E+00 -4.6341877988956215E+00 -4.6519480488798441E+00 -4.6689870415479158E+00 -4.6851887984967098E+00 -4.7004428963660558E+00 -4.7146461221230336E+00 -4.7277038469865937E+00 -4.7395310570641787E+00 -4.7500529962095275E+00 -4.7592053971902475E+00 -4.7669342995827408E+00 -4.7731954753465349E+00 -4.7779535040980283E+00 -4.7811805582531752E+00 -4.7828549722206137E+00 -4.7829596788945734E+00 -4.7814806003177575E+00 -4.7784050776607865E+00 -4.7737204190425926E+00 -4.7674126329029667E+00 -4.7594654007193284E+00 -4.7498593269584681E+00 -4.7385714873950553E+00 -4.7255752803423414E+00 -4.7108405698863560E+00 -4.6943340964800608E+00 -4.6760201187222581E+00 -4.6558612410969848E+00 -4.6338193758627551E+00 -4.6098567831760553E+00 -4.5839371316513757E+00 -4.5560265216841938E+00 -4.5260944157022971E+00 -4.4941144227085079E+00 -4.4600648886701650E+00 -4.4239292490700137E+00 -4.3856961048861303E+00 -4.3453589879379226E+00 -4.3029157855955456E+00 -4.2583677980940227E+00 -4.2117184041456612E+00 -4.1629713126664507E+00 -4.1121283811920559E+00 -4.0591869866354360E+00 -4.0041369438538066E+00 -3.9469569852373492E+00 -3.8876108440056871E+00 -3.8260430290712231E+00 -3.7621744436524169E+00 -3.6958980851610028E+00 -3.6270751689290193E+00 -3.5555321368575181E+00 -3.4810591310533696E+00 -3.4034106108316964E+00 -3.3223088399324423E+00 -3.2374509346194080E+00 -3.1485200078553253E+00 -3.0552006449239970E+00 -2.9571984982875974E+00 -2.8542632241965880E+00 -2.7462133711327268E+00 -2.6329612782346086E+00 -2.5145356779807706E+00 -2.3910996384112044E+00 -2.2629617951726755E+00 -2.1305795031441597E+00 -1.9945534818432415E+00 -1.8556145655004910E+00 -1.7146040942245022E+00 -1.5724501180403412E+00 -1.4301418240604487E+00 -1.2887044282393609E+00 -1.1491762762774564E+00 -1.0125892103449703E+00 -8.7995253172344612E-01 -7.5224025377474291E-01 -6.3038087858894709E-01 -5.1524867664150664E-01 -4.0765539106681298E-01 -3.0834138779374864E-01 -2.1796547808022046E-01 -1.3709289857806303E-01 -6.6181200930619036E-02 -5.5640455117355863E-03 4.4566903616635144E-02 8.4181617903413525E-02 1.1343234971141729E-01 1.3267453837340165E-01 1.4248687555748699E-01 1.4368883420659906E-01 1.3735303066298243E-01 1.2480842989417987E-01 1.0762856638246031E-01 8.7596623796535072E-02 6.6634336482065792E-02 4.6711817169847666E-02 2.9643861374749926E-02 1.6193196179630106E-02 6.2984158510223636E-03 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 </zero_potential> <blochl_local_ionic_potential grid="log1" rc=" 2.3114501246901900"> -4.1445702397282197E+01 -4.1445702394423812E+01 -4.1445702391861751E+01 -4.1445702388558040E+01 -4.1445702383947847E+01 -4.1445702377939440E+01 -4.1445702370297390E+01 -4.1445702361073131E+01 -4.1445702350251750E+01 -4.1445702337590234E+01 -4.1445702323115576E+01 -4.1445702306681575E+01 -4.1445702288257600E+01 -4.1445702267706601E+01 -4.1445702244922579E+01 -4.1445702219853963E+01 -4.1445702192327445E+01 -4.1445702162276319E+01 -4.1445702129566470E+01 -4.1445702094072487E+01 -4.1445702055703336E+01 -4.1445702014320936E+01 -4.1445701969773950E+01 -4.1445701921926208E+01 -4.1445701870668643E+01 -4.1445701815797079E+01 -4.1445701757215382E+01 -4.1445701694717009E+01 -4.1445701628170070E+01 -4.1445701557391857E+01 -4.1445701482191637E+01 -4.1445701402394839E+01 -4.1445701317807014E+01 -4.1445701228212030E+01 -4.1445701133449255E+01 -4.1445701033257095E+01 -4.1445700927441798E+01 -4.1445700815743791E+01 -4.1445700697960881E+01 -4.1445700573816062E+01 -4.1445700443069107E+01 -4.1445700305440255E+01 -4.1445700160663442E+01 -4.1445700008430421E+01 -4.1445699848483038E+01 -4.1445699680465758E+01 -4.1445699504103814E+01 -4.1445699319028165E+01 -4.1445699124928176E+01 -4.1445698921408848E+01 -4.1445698708150793E+01 -4.1445698484722236E+01 -4.1445698250771798E+01 -4.1445698005838928E+01 -4.1445697749549645E+01 -4.1445697481412353E+01 -4.1445697201023087E+01 -4.1445696907856338E+01 -4.1445696601464455E+01 -4.1445696281296577E+01 -4.1445695946871155E+01 -4.1445695597597400E+01 -4.1445695232953454E+01 -4.1445694852304719E+01 -4.1445694455096145E+01 -4.1445694040640980E+01 -4.1445693608346737E+01 -4.1445693157477656E+01 -4.1445692687399060E+01 -4.1445692197317797E+01 -4.1445691686556117E+01 -4.1445691154258640E+01 -4.1445690599700747E+01 -4.1445690021970350E+01 -4.1445689420275343E+01 -4.1445688793643605E+01 -4.1445688141237810E+01 -4.1445687462003704E+01 -4.1445686755044328E+01 -4.1445686019232816E+01 -4.1445685253599613E+01 -4.1445684456945223E+01 -4.1445683628221630E+01 -4.1445682766147200E+01 -4.1445681869597522E+01 -4.1445680937199590E+01 -4.1445679967749186E+01 -4.1445678959768422E+01 -4.1445677911970243E+01 -4.1445676822771041E+01 -4.1445675690786558E+01 -4.1445674514323713E+01 -4.1445673291898444E+01 -4.1445672021696474E+01 -4.1445670702119905E+01 -4.1445669331229574E+01 -4.1445667907316292E+01 -4.1445666428297528E+01 -4.1445664892341860E+01 -4.1445663297218111E+01 -4.1445661640962072E+01 -4.1445659921186895E+01 -4.1445658135782352E+01 -4.1445656282192715E+01 -4.1445654358156915E+01 -4.1445652360937110E+01 -4.1445650288111601E+01 -4.1445648136746172E+01 -4.1445645904243356E+01 -4.1445643587462285E+01 -4.1445641183618157E+01 -4.1445638689348449E+01 -4.1445636101668612E+01 -4.1445633416977365E+01 -4.1445630632075030E+01 -4.1445627743105753E+01 -4.1445624746639403E+01 -4.1445621638547792E+01 -4.1445618415158854E+01 -4.1445615072047723E+01 -4.1445611605279183E+01 -4.1445608010117979E+01 -4.1445604282347716E+01 -4.1445600416896710E+01 -4.1445596409246868E+01 -4.1445592253968783E+01 -4.1445587946220954E+01 -4.1445583480192518E+01 -4.1445578850696414E+01 -4.1445574051508125E+01 -4.1445569077073820E+01 -4.1445563920729775E+01 -4.1445558576523595E+01 -4.1445553037323982E+01 -4.1445547296753737E+01 -4.1445541347178597E+01 -4.1445535181768108E+01 -4.1445528792348178E+01 -4.1445522171603805E+01 -4.1445515310784081E+01 -4.1445508202054079E+01 -4.1445500836045824E+01 -4.1445493204369328E+01 -4.1445485296995471E+01 -4.1445477104938860E+01 -4.1445468617464236E+01 -4.1445459824948088E+01 -4.1445450715898239E+01 -4.1445441280010741E+01 -4.1445431504983027E+01 -4.1445421379780932E+01 -4.1445410891236307E+01 -4.1445400027532479E+01 -4.1445388774574823E+01 -4.1445377119711210E+01 -4.1445365047853230E+01 -4.1445352545454440E+01 -4.1445339596365294E+01 -4.1445326186079406E+01 -4.1445312297311681E+01 -4.1445297914531459E+01 -4.1445283019236875E+01 -4.1445267594798707E+01 -4.1445251621415728E+01 -4.1445235081282199E+01 -4.1445217953204470E+01 -4.1445200218120704E+01 -4.1445181853346362E+01 -4.1445162838474182E+01 -4.1445143149224073E+01 -4.1445122763749303E+01 -4.1445101656063322E+01 -4.1445079802776796E+01 -4.1445057176078038E+01 -4.1445033750926861E+01 -4.1445009497557542E+01 -4.1444984389165263E+01 -4.1444958393892023E+01 -4.1444931483042204E+01 -4.1444903622520457E+01 -4.1444874781609073E+01 -4.1444844923817364E+01 -4.1444814016261688E+01 -4.1444782019888990E+01 -4.1444748899499004E+01 -4.1444714613295268E+01 -4.1444679123597922E+01 -4.1444642385675515E+01 -4.1444604359192688E+01 -4.1444564996278260E+01 -4.1444524253755660E+01 -4.1444482080391509E+01 -4.1444438429969594E+01 -4.1444393247659022E+01 -4.1444346483988348E+01 -4.1444298080277612E+01 -4.1444247983571863E+01 -4.1444196131070711E+01 -4.1444142466092046E+01 -4.1444086921425416E+01 -4.1444029436398033E+01 -4.1443969939080787E+01 -4.1443908364529840E+01 -4.1443844635764961E+01 -4.1443778683271454E+01 -4.1443710424663259E+01 -4.1443639785532127E+01 -4.1443566677707416E+01 -4.1443491021541867E+01 -4.1443412722673457E+01 -4.1443331695848187E+01 -4.1443247840076850E+01 -4.1443161064103080E+01 -4.1443071259844388E+01 -4.1442978329619343E+01 -4.1442882157752848E+01 -4.1442782639686094E+01 -4.1442679651616324E+01 -4.1442573081621575E+01 -4.1442462797200136E+01 -4.1442348678546473E+01 -4.1442230583847184E+01 -4.1442108384856716E+01 -4.1441981929793336E+01 -4.1441851081375518E+01 -4.1441715677149730E+01 -4.1441575570159301E+01 -4.1441430586526280E+01 -4.1441280568934133E+01 -4.1441125331273582E+01 -4.1440964705134768E+01 -4.1440798491313032E+01 -4.1440626509518758E+01 -4.1440448546525879E+01 -4.1440264409322353E+01 -4.1440073869668439E+01 -4.1439876720926534E+01 -4.1439672718779441E+01 -4.1439461641995720E+01 -4.1439243229041296E+01 -4.1439017243051808E+01 -4.1438783404054718E+01 -4.1438541458439474E+01 -4.1438291106484932E+01 -4.1438032076639630E+01 -4.1437764048029429E+01 -4.1437486729880774E+01 -4.1437199778659846E+01 -4.1436902882996080E+01 -4.1436595675080511E+01 -4.1436277821469304E+01 -4.1435948928345390E+01 -4.1435608638608102E+01 -4.1435256530571756E+01 -4.1434892221777829E+01 -4.1434515260676463E+01 -4.1434125237624336E+01 -4.1433721669064710E+01 -4.1433304116207964E+01 -4.1432872061189450E+01 -4.1432425033964321E+01 -4.1431962479889940E+01 -4.1431483895400234E+01 -4.1430988686420214E+01 -4.1430476313426674E+01 -4.1429946140060558E+01 -4.1429397588221434E+01 -4.1428829976201598E+01 -4.1428242684504973E+01 -4.1427634982780674E+01 -4.1427006207104121E+01 -4.1426355574938825E+01 -4.1425682374667780E+01 -4.1424985767758216E+01 -4.1424264991386423E+01 -4.1423519146924555E+01 -4.1422747416557101E+01 -4.1421948837150580E+01 -4.1421122531820906E+01 -4.1420267468181827E+01 -4.1419382705888296E+01 -4.1418467138191822E+01 -4.1417519756553006E+01 -4.1416539374360688E+01 -4.1415524909780736E+01 -4.1414475090417945E+01 -4.1413388755646650E+01 -4.1412264540913689E+01 -4.1411101200879443E+01 -4.1409897271972973E+01 -4.1408651417760829E+01 -4.1407362068274260E+01 -4.1406027789117076E+01 -4.1404646895986652E+01 -4.1403217849133945E+01 -4.1401738841395797E+01 -4.1400208219726530E+01 -4.1398624044950871E+01 -4.1396984542200492E+01 -4.1395287630479608E+01 -4.1393531403961774E+01 -4.1391713629339300E+01 -4.1389832260063429E+01 -4.1387884899319587E+01 -4.1385869349432831E+01 -4.1383783038174982E+01 -4.1381623605703929E+01 -4.1379388291766453E+01 -4.1377074562696649E+01 -4.1374679456929584E+01 -4.1372200254750567E+01 -4.1369633779380344E+01 -4.1366977112345388E+01 -4.1364226847233418E+01 -4.1361379853746108E+01 -4.1358432481056767E+01 -4.1355381373811113E+01 -4.1352222621847154E+01 -4.1348952631628102E+01 -4.1345567218908371E+01 -4.1342062539317247E+01 -4.1338434120375261E+01 -4.1334677855198578E+01 -4.1330788970087781E+01 -4.1326763085592454E+01 -4.1322595115710634E+01 -4.1318280400840983E+01 -4.1313813534446687E+01 -4.1309189572729437E+01 -4.1304402784425903E+01 -4.1299447942363010E+01 -4.1294318991867158E+01 -4.1289010429701044E+01 -4.1283515886373046E+01 -4.1277829598306106E+01 -4.1271944899132151E+01 -4.1265855791294172E+01 -4.1259555341185767E+01 -4.1253037356724697E+01 -4.1246294680934476E+01 -4.1239320982325800E+01 -4.1232108941189615E+01 -4.1224652159847537E+01 -4.1216943235495023E+01 -4.1208975797482012E+01 -4.1200742459958200E+01 -4.1192236993253402E+01 -4.1183452148755876E+01 -4.1174381971091947E+01 -4.1165019486524784E+01 -4.1155359161869320E+01 -4.1145394446121593E+01 -4.1135120380768690E+01 -4.1124530982227760E+01 -4.1113622006298577E+01 -4.1102388156207866E+01 -4.1090826001312699E+01 -4.1078930992067441E+01 -4.1066700529718254E+01 -4.1054130765421455E+01 -4.1041219813740845E+01 -4.1027964308753290E+01 -4.1014362750121407E+01 -4.1000411784986497E+01 -4.0986109672088411E+01 -4.0971452255689712E+01 -4.0956436532039355E+01 -4.0941056282164361E+01 -4.0925305727817857E+01 -4.0909174795884866E+01 -4.0892652860094863E+01 -4.0875723623318052E+01 -4.0858368958896314E+01 -4.0840563420053670E+01 -4.0822278221774511E+01 -4.0803475419059616E+01 -4.0784112105622683E+01 -4.0764134341885509E+01 -4.0743481685465177E+01 -4.0722080988580323E+01 -4.0699851407995730E+01 -4.0676698218550897E+01 -4.0652518463912905E+01 -4.0627194934431238E+01 -4.0600602601046404E+01 -4.0572602869558636E+01 -4.0543050879307216E+01 -4.0511790067913630E+01 -4.0478660315546364E+01 -4.0443492743164775E+01 -4.0406118558827565E+01 -4.0366363892381301E+01 -4.0324059082538142E+01 -4.0279033256524208E+01 -4.0231123721691745E+01 -4.0180169964379871E+01 -4.0126022806974731E+01 -4.0068537547189713E+01 -4.0007582620428408E+01 -3.9943031725787002E+01 -3.9874771877889962E+01 -3.9802694540297580E+01 -3.9726703121384922E+01 -3.9646703313561517E+01 -3.9562610235351869E+01 -3.9474338308704361E+01 -3.9381808333000393E+01 -3.9284937291194652E+01 -3.9183645641295378E+01 -3.9077847418863676E+01 -3.8967457954311641E+01 -3.8852384552518693E+01 -3.8732534717058435E+01 -3.8607807570104441E+01 -3.8478102522132822E+01 -3.8343311480518864E+01 -3.8203327775443555E+01 -3.8058039118029932E+01 -3.7907336498061682E+01 -3.7751107803549388E+01 -3.7589246348960806E+01 -3.7421645057979802E+01 -3.7248204258784860E+01 -3.7068826353797689E+01 -3.6883422522814712E+01 -3.6691907847422627E+01 -3.6494206582359155E+01 -3.6290247755330064E+01 -3.6079968689300166E+01 -3.5863311147398889E+01 -3.5640222803039130E+01 -3.5410654036386141E+01 -3.5174557055191229E+01 -3.4931883483243979E+01 -3.4682580858333139E+01 -3.4426591227456527E+01 -3.4163844856324978E+01 -3.3894260248298139E+01 -3.3617735200377957E+01 -3.3334149106857240E+01 -3.3043352095478745E+01 -3.2745171225235055E+01 -3.2439399317338847E+01 -3.2125807559065123E+01 -3.1804136477133529E+01 -3.1474117959555855E+01 -3.1135470822792751E+01 -3.0787934402513944E+01 -3.0431269352295249E+01 -3.0065301942724446E+01 -2.9689926828817065E+01 -2.9305156599803929E+01 -2.8911118896827720E+01 -2.8508102254362345E+01 -2.8096538529433090E+01 -2.7677037056689198E+01 -2.7250347325038216E+01 -2.6817379567704656E+01 -2.6379150298473260E+01 -2.5936794777936360E+01 -2.5491504130336445E+01 -2.5044538336431945E+01 -2.4597164173297642E+01 -2.4150674747754554E+01 -2.3706333247085293E+01 -2.3265399443305551E+01 -2.2829079220363710E+01 -2.2398553988941529E+01 -2.1974933342587793E+01 -2.1559281802843508E+01 -2.1152572262607343E+01 -2.0755705382435512E+01 -2.0369463457224935E+01 -1.9994519619046699E+01 -1.9631393946439282E+01 -1.9280451254480617E+01 -1.8941862928466975E+01 -1.8615593421127077E+01 -1.8301373031804566E+01 -1.7998675735646952E+01 -1.7706712101573579E+01 -1.7424407541797613E+01 -1.7150433707883316E+01 -1.6883209434293644E+01 -1.6621007348848682E+01 -1.6361993642497829E+01 -1.6104484176940218E+01 -1.5847774181227726E+01 -1.5591979839574442E+01 -1.5337031492396374E+01 -1.5080189089399552E+01 -1.4827667287432165E+01 -1.4579391825535227E+01 -1.4335288717887254E+01 -1.4095285263431952E+01 -1.3859310752303308E+01 -1.3627295691526140E+01 -1.3399172324548552E+01 -1.3174874052671090E+01 -1.2954335810438744E+01 -1.2737493638229056E+01 -1.2524284948210893E+01 -1.2314648211919989E+01 -1.2108523144460101E+01 -1.1905850478228626E+01 -1.1706572087039969E+01 -1.1510630823413734E+01 -1.1317970599303417E+01 -1.1128536269565128E+01 -1.0942273681901371E+01 -1.0759129593369586E+01 -1.0579051698900567E+01 -1.0401988571088630E+01 -1.0227889674104539E+01 -1.0056705319651575E+01 -9.8883866711489610E+00 -9.7228857107594582E+00 -9.5601552372625367E+00 -9.4001488405735980E+00 -9.2428208956569229E+00 -9.0881265420681991E+00 -8.9360216754885879E+00 -8.7864629306208943E+00 -8.6394076713858574E+00 -8.4948139760638206E+00 -8.3526406268225326E+00 -8.2128470963827418E+00 -8.0753935372966215E+00 -7.9402407696758495E+00 -7.8073502704755775E+00 -7.6766841619944906E+00 -7.5482052013138041E+00 -7.4218767693889509E+00 -7.2976628607270708E+00 -7.1755280729590138E+00 -7.0554375967986696E+00 -6.9373572060262392E+00 -6.8212532477489880E+00 -6.7070926327522820E+00 -6.5948428260674534E+00 -6.4844718376620083E+00 -6.3759482133128857E+00 -6.2692410256157105E+00 -6.1643198651576938E+00 -6.0611548318306774E+00 -5.9597165262959653E+00 -5.8599760415887214E+00 -5.7619049548659991E+00 -5.6654753192916774E+00 -5.5706596560587807E+00 -5.4774309465450157E+00 -5.3857626246004813E+00 -5.2956285689645251E+00 -5.2070030958100419E+00 -5.1198609514128703E+00 -5.0341773049442020E+00 -4.9499277413839344E+00 -4.8670882545529750E+00 -4.7856352402624216E+00 -4.7055454895777276E+00 -4.6267961821958536E+00 -4.5493648799335622E+00 -4.4732295203248951E+00 -4.3983684103261593E+00 -4.3247602201264108E+00 -4.2523839770618315E+00 -4.1812190596321477E+00 -4.1112451916174324E+00 -4.0424424362935758E+00 -3.9747911907447704E+00 -3.9082721802714020E+00 -3.8428664528916658E+00 -3.7785553739354842E+00 -3.7153206207289942E+00 -3.6531441773682172E+00 -3.5920083295803438E+00 -3.5318956596711950E+00 -3.4727890415573954E+00 -3.4146716358818341E+00 -3.3575268852110374E+00 -3.3013385093130148E+00 -3.2460905005143466E+00 -3.1917671191350361E+00 -3.1383528889999246E+00 -3.0858325930253470E+00 -3.0341912688797654E+00 -2.9834142047171404E+00 -2.9334869349818202E+00 -2.8843952362837535E+00 -2.8361251233428066E+00 -2.7886628450011157E+00 -2.7419948803022098E+00 -2.6961079346358878E+00 -2.6509889359476810E+00 -2.6066250310118573E+00 -2.5630035817668735E+00 -2.5201121617122477E+00 -2.4779385523657838E+00 -2.4364707397802170E+00 -2.3956969111181765E+00 -2.3556054512845628E+00 -2.3161849396153547E+00 -2.2774241466218901E+00 -2.2393120307897041E+00 -2.2018377354309973E+00 -2.1649905855898486E+00 -2.1287600849992541E+00 -2.0931359130891920E+00 -2.0581079220447731E+00 -2.0236661339136917E+00 -1.9898007377621392E+00 -1.9565020868783576E+00 -1.9237606960230431E+00 -1.8915672387258093E+00 -1.8599125446269462E+00 -1.8287875968636873E+00 -1.7981835295002964E+00 -1.7680916250011687E+00 -1.7385033117462745E+00 -1.7094101615882189E+00 -1.6808038874502185E+00 -1.6526763409643126E+00 -1.6250195101491360E+00 -1.5978255171265829E+00 -1.5710866158767101E+00 -1.5447951900302608E+00 -1.5189437506981420E+00 -1.4935249343372616E+00 -1.4685315006521082E+00 -1.4439563305314742E+00 -1.4197924240197355E+00 -1.3960328983221053E+00 -1.3726709858432966E+00 -1.3497000322590196E+00 -1.3271134946197998E+00 -1.3049049394865244E+00 -1.2830680410972262E+00 -1.2615965795645621E+00 -1.2404844391034766E+00 -1.2197256062885464E+00 -1.1993141683405042E+00 -1.1792443114414570E+00 -1.1595103190783098E+00 -1.1401065704139441E+00 -1.1210275386856534E+00 -1.1022677896304058E+00 -1.0838219799364708E+00 -1.0656848557209764E+00 -1.0478512510329523E+00 -1.0303160863814469E+00 -1.0130743672882725E+00 -9.9612118286500717E-01 -9.7945170441380069E-01 -9.6306118405161734E-01 -9.4694495335751216E-01 -9.3109842204255511E-01 -9.1551707664202508E-01 -9.0019647922949775E-01 -8.8513226615246887E-01 -8.7032014678913361E-01 -8.5575590232599852E-01 -8.4143538455594313E-01 -8.2735451469641141E-01 -8.1350928222738705E-01 -7.9989574374882433E-01 -7.8651002185720609E-01 -7.7334830404091059E-01 -7.6040684159407246E-01 -7.4768194854861969E-01 -7.3517000062420379E-01 -7.2286743419569544E-01 -7.1077074527797146E-01 -6.9887648852769646E-01 -6.8718127626181480E-01 -6.7568177749247349E-01 -6.6437471697810180E-01 -6.5325687429037538E-01 -6.4232508289679657E-01 -6.3157622925864110E-01 -6.2100725194399520E-01 -6.1061514075564649E-01 -6.0039693587357057E-01 -5.9034972701177590E-01 -5.8047065258925834E-01 -5.7075689891483627E-01 -5.6120569938563236E-01 -5.5181433369896549E-01 -5.4258012707744607E-01 -5.3350044950703235E-01 -5.2457271498784697E-01 -5.1579438079753082E-01 -5.0716294676692986E-01 -4.9867595456790537E-01 -4.9033098701306532E-01 -4.8212566736721441E-01 -4.7405765867033700E-01 -4.6612466307190459E-01 -4.5832442117632960E-01 -4.5065471139937435E-01 -4.4311334933533336E-01 </blochl_local_ionic_potential> <ae_partial_wave state= "Ni1" grid="log1"> -1.0286195540600799E+01 -1.0059933740237765E+01 -9.9091090813255747E+00 -9.8199085942020048E+00 -9.7556658258516009E+00 -9.6568608399056739E+00 -9.6121855528666842E+00 -9.5775504182183280E+00 -9.5452824662702547E+00 -9.5165990011775801E+00 -9.4904637563689818E+00 -9.4663180055477358E+00 -9.4438283109519432E+00 -9.4227179069195888E+00 -9.4027703310766864E+00 -9.3838160671993123E+00 -9.3657180123657078E+00 -9.3483639118996287E+00 -9.3316607066021593E+00 -9.3155303242399921E+00 -9.2999065897960342E+00 -9.2847328951709667E+00 -9.2699604103783848E+00 -9.2555466946512226E+00 -9.2414546040622714E+00 -9.2276514226405340E+00 -9.2141081642174676E+00 -9.2007990062061555E+00 -9.1877008264417768E+00 -9.1747928213364034E+00 -9.1620561887787275E+00 -9.1494738630235819E+00 -9.1370302916573998E+00 -9.1247112468652087E+00 -9.1125036648515820E+00 -9.1003955085168258E+00 -9.0883756494563563E+00 -9.0764337661056675E+00 -9.0645602554468994E+00 -9.0527461561626179E+00 -9.0409830814975365E+00 -9.0292631603892346E+00 -9.0175789856717739E+00 -9.0059235683532357E+00 -8.9942902971286802E+00 -8.9826729024223244E+00 -8.9710654243609866E+00 -8.9594621841712119E+00 -8.9478577585671264E+00 -8.9362469567586800E+00 -8.9246247997622685E+00 -8.9129865017398853E+00 -8.9013274531302038E+00 -8.8896432053664913E+00 -8.8779294570032814E+00 -8.8661820410964562E+00 -8.8543969137011285E+00 -8.8425701433685298E+00 -8.8306979015375635E+00 -8.8187764537292104E+00 -8.8068021514628647E+00 -8.7947714248230060E+00 -8.7826807756127518E+00 -8.7705267710381367E+00 -8.7583060378729982E+00 -8.7460152570599199E+00 -8.7336511587074721E+00 -8.7212105174481493E+00 -8.7086901481251981E+00 -8.6960869017797524E+00 -8.6833976619126290E+00 -8.6706193409977246E+00 -8.6577488772261848E+00 -8.6447832314626574E+00 -8.6317193843966695E+00 -8.6185543338738348E+00 -8.6052850923930180E+00 -8.5919086847569446E+00 -8.5784221458648382E+00 -8.5648225186367775E+00 -8.5511068520603679E+00 -8.5372721993512304E+00 -8.5233156162194810E+00 -8.5092341592351985E+00 -8.4950248842864351E+00 -8.4806848451238750E+00 -8.4662110919868230E+00 -8.4516006703056856E+00 -8.4368506194764574E+00 -8.4219579717031969E+00 -8.4069197509048372E+00 -8.3917329716829467E+00 -8.3763946383474206E+00 -8.3609017439973137E+00 -8.3452512696543160E+00 -8.3294401834466054E+00 -8.3134654398409982E+00 -8.2973239789215647E+00 -8.2810127257130297E+00 -8.2645285895474352E+00 -8.2478684634727983E+00 -8.2310292237024978E+00 -8.2140077291044076E+00 -8.1968008207288339E+00 -8.1794053213744498E+00 -8.1618180351915779E+00 -8.1440357473222456E+00 -8.1260552235765289E+00 -8.1078732101448097E+00 -8.0894864333457033E+00 -8.0708915994094124E+00 -8.0520853942964106E+00 -8.0330644835514491E+00 -8.0138255121928594E+00 -7.9943651046373381E+00 -7.9746798646603123E+00 -7.9547663753921958E+00 -7.9346211993507962E+00 -7.9142408785102401E+00 -7.8936219344068679E+00 -7.8727608682825343E+00 -7.8516541612658868E+00 -7.8302982745921632E+00 -7.8086896498622185E+00 -7.7868247093413290E+00 -7.7646998562986962E+00 -7.7423114753882425E+00 -7.7196559330716772E+00 -7.6967295780845779E+00 -7.6735287419465186E+00 -7.6500497395161080E+00 -7.6262888695919644E+00 -7.6022424155607355E+00 -7.5779066460930924E+00 -7.5532778158890039E+00 -7.5283521664732636E+00 -7.5031259270426247E+00 -7.4775953153656278E+00 -7.4517565387365359E+00 -7.4256057949845093E+00 -7.3991392735395305E+00 -7.3723531565562990E+00 -7.3452436200975670E+00 -7.3178068353783603E+00 -7.2900389700724606E+00 -7.2619361896827446E+00 -7.2334946589767881E+00 -7.2047105434893703E+00 -7.1755800110933503E+00 -7.1460992336406024E+00 -7.1162643886745096E+00 -7.0860716612157670E+00 -7.0555172456230313E+00 -7.0245973475301406E+00 -6.9933081858616060E+00 -6.9616459949279870E+00 -6.9296070266029597E+00 -6.8971875525836781E+00 -6.8643838667362687E+00 -6.8311922875280580E+00 -6.7976091605483546E+00 -6.7636308611194904E+00 -6.7292537969997452E+00 -6.6944744111800372E+00 -6.6592891847759104E+00 -6.6236946400166277E+00 -6.5876873433329521E+00 -6.5512639085453426E+00 -6.5144210001540959E+00 -6.4771553367331141E+00 -6.4394636944288077E+00 -6.4013429105656483E+00 -6.3627898873598827E+00 -6.3238015957427862E+00 -6.2843750792949127E+00 -6.2445074582925297E+00 -6.2041959338676245E+00 -6.1634377922825658E+00 -6.1222304093205837E+00 -6.0805712547930169E+00 -6.0384578971643625E+00 -5.9958880082958474E+00 -5.9528593683083377E+00 -5.9093698705651549E+00 -5.8654175267753068E+00 -5.8210004722175350E+00 -5.7761169710853482E+00 -5.7307654219532056E+00 -5.6849443633637318E+00 -5.6386524795357680E+00 -5.5918886061928479E+00 -5.5446517365115451E+00 -5.4969410271888650E+00 -5.4487558046278002E+00 -5.4000955712397651E+00 -5.3509600118625720E+00 -5.3013490002922969E+00 -5.2512626059271117E+00 -5.2007011005209947E+00 -5.1496649650448312E+00 -5.0981548966523107E+00 -5.0461718157475062E+00 -4.9937168731509693E+00 -4.9407914573606133E+00 -4.8873972019035232E+00 -4.8335359927743280E+00 -4.7792099759555402E+00 -4.7244215650147998E+00 -4.6691734487736127E+00 -4.6134685990417950E+00 -4.5573102784113360E+00 -4.5007020481031024E+00 -4.4436477758591817E+00 -4.3861516438733981E+00 -4.3282181567518778E+00 -4.2698521494952191E+00 -4.2110587954931678E+00 -4.1518436145223099E+00 -4.0922124807366984E+00 -4.0321716306407511E+00 -3.9717276710333294E+00 -3.9108875869111488E+00 -3.8496587493192687E+00 -3.7880489231356678E+00 -3.7260662747764011E+00 -3.6637193798071288E+00 -3.6010172304462409E+00 -3.5379692429441061E+00 -3.4745852648223288E+00 -3.4108755819562715E+00 -3.3468509254833356E+00 -3.2825224785189229E+00 -3.2179018826612040E+00 -3.1530012442652322E+00 -3.0878331404661461E+00 -3.0224106249305862E+00 -2.9567472333147080E+00 -2.8908569884064952E+00 -2.8247544049294033E+00 -2.7584544939836424E+00 -2.6919727671007858E+00 -2.6253252398867000E+00 -2.5585284352271418E+00 -2.4915993860298125E+00 -2.4245556374759532E+00 -2.3574152487541009E+00 -2.2901967942479979E+00 -2.2229193641502345E+00 -2.1556025644726358E+00 -2.0882665164240635E+00 -2.0209318551259154E+00 -1.9536197276352432E+00 -1.8863517902452420E+00 -1.8191502050325490E+00 -1.7520376356207554E+00 -1.6850372421294200E+00 -1.6181726752779064E+00 -1.5514680696134238E+00 -1.4849480358328160E+00 -1.4186376521678974E+00 -1.3525624548043940E+00 -1.2867484273049716E+00 -1.2212219890072338E+00 -1.1560099823681151E+00 -1.0911396592266498E+00 -1.0266386659577318E+00 -9.6253502749014441E-01 -8.9885713016289204E-01 -8.3563370339464116E-01 -7.7289380014192433E-01 -7.1066677612270657E-01 -6.4898226778292056E-01 -5.8787016898478517E-01 -5.2736060639708837E-01 -4.6748391356931090E-01 -4.0827060367349544E-01 -3.4975134090037019E-01 -2.9195691049945549E-01 -2.3491818745696333E-01 -1.7866610381036438E-01 -1.2323161460474939E-01 -6.8645662503653254E-02 -1.4939141075911808E-02 3.7857143209657100E-02 8.9712510238617663E-02 1.4059644669911373E-01 1.9047864765646189E-01 2.3932905917515165E-01 2.8711792189937513E-01 3.3381581549611511E-01 3.7939370386160237E-01 4.2382298099356436E-01 4.6707551743870557E-01 5.0912370723732581E-01 5.4994051530439780E-01 5.8949952520749349E-01 6.2777498732493819E-01 6.6474186739020946E-01 7.0037589544860035E-01 7.3465361526728168E-01 7.6755243424825503E-01 7.9905067389386952E-01 8.2912762086574288E-01 8.5776357865966835E-01 8.8493991989155718E-01 9.1063913915346706E-01 9.3484490635580941E-01 9.5754212042455700E-01 9.7871696317418466E-01 9.9835695313257034E-01 1.0164509990574644E+00 1.0329894528591554E+00 1.0479641616324922E+00 1.0613685185033748E+00 1.0731975120079518E+00 1.0834477737431687E+00 1.0921176240508474E+00 1.0992071155200145E+00 1.1047180741110703E+00 1.1086541377191328E+00 1.1110207920026154E+00 1.1118254033076544E+00 1.1110772485210114E+00 1.1087875416850705E+00 1.1049694572098323E+00 1.0996381495194092E+00 1.0928107689747979E+00 1.0845064739208612E+00 1.0747464387132006E+00 1.0635538575897099E+00 1.0509539442615694E+00 1.0369739271089959E+00 1.0216430398777767E+00 1.0049925077834196E+00 9.8705552894035864E-01 9.6786725104410143E-01 9.4746474324446117E-01 9.2588696315806152E-01 9.0317471897830570E-01 8.7937062665091104E-01 8.5451906209310335E-01 8.2866610844465427E-01 8.0185949834929959E-01 7.7414855127571192E-01 7.4558410589828095E-01 7.1621844756960074E-01 6.8610523092883091E-01 6.5529939770326884E-01 6.2385708977453280E-01 5.9183555759603634E-01 5.5929306406494639E-01 5.2628878396983692E-01 4.9288269915479171E-01 4.5913548956192646E-01 4.2510842033711344E-01 3.9086322520804551E-01 3.5646198636936283E-01 3.2196701113597209E-01 2.8744070565224356E-01 2.5294544597057378E-01 2.1854344683674140E-01 1.8429662854017481E-01 1.5026648220325442E-01 1.1651393389361012E-01 8.3099207945912634E-02 5.0081689874366821E-02 1.7519789244669730E-02 -1.4529197142884583E-02 -4.6009221424073488E-02 -7.6865619867661578E-02 -1.0704524675697633E-01 -1.3649660656226148E-01 -1.6516998389994714E-01 -1.9301757058832753E-01 -2.1999358883341039E-01 -2.4605440921738866E-01 -2.7115866174651510E-01 -2.9526733781463244E-01 -3.1834388066551761E-01 -3.4035426193733032E-01 -3.6126704229765966E-01 -3.8105341514472901E-01 -3.9968723388728361E-01 -4.1714502531711967E-01 -4.3340599377926126E-01 -4.4845202275315382E-01 -4.6226768143599045E-01 -4.7484024326428931E-01 -4.8615972057287260E-01 -4.9621891500640536E-01 -5.0501347803889296E-01 -5.1254197184121664E-01 -5.1880591936879339E-01 -5.2380983438110873E-01 -5.2756122618611878E-01 -5.3007057843535499E-01 -5.3135130469802905E-01 -5.3141968515001559E-01 -5.3029478877451319E-01 -5.2799838465677795E-01 -5.2455484487996673E-01 -5.1999104055240253E-01 -5.1433623175542054E-01 -5.0762195171023883E-01 -4.9988188519012355E-01 -4.9115174110670184E-01 -4.8146911923289987E-01 -4.7087337114805966E-01 -4.5940545566520319E-01 -4.4710778919272315E-01 -4.3402409166635664E-01 -4.2019922884354616E-01 -4.0567905187071374E-01 -3.9051023511120575E-01 -3.7474011325949380E-01 -3.5841651877070480E-01 -3.4158762061016279E-01 -3.2430176528200699E-01 -3.0660732103508853E-01 -2.8855252607322224E-01 -2.7018534151940971E-01 -2.5155330980277535E-01 -2.3270341905485295E-01 -2.1368197402006944E-01 -1.9453447390498099E-01 -1.7530549751286376E-01 -1.5603859593538580E-01 -1.3677619300182473E-01 -1.1755949361916532E-01 -9.8428400073809555E-02 -7.9421436307940380E-02 -6.0575680131051871E-02 -4.1926703280015951E-02 -2.3508519199405990E-02 -5.3535383776521575E-03 1.2507468956114605E-02 3.0045402995164412E-02 4.7232857619408979E-02 6.4044137017998881E-02 8.0455265939481893E-02 9.6443993847241699E-02 1.1198979326362277E-01 1.2707385258965617E-01 1.4167906368932759E-01 1.5579000452855926E-01 1.6939291715997357E-01 1.8247568134577619E-01 1.9502778411288865E-01 2.0704028553689471E-01 2.1850578105471569E-01 2.2941836060941218E-01 2.3977356493402754E-01 2.4956833928403582E-01 2.5880098492865816E-01 2.6747110870942031E-01 2.7557957096844538E-01 2.8312843213849487E-01 2.9012089827092935E-01 2.9656126575626462E-01 3.0245486546528288E-01 3.0780800650754192E-01 3.1262791977038978E-01 3.1692270136762885E-01 3.2070125609591643E-01 3.2397324097246177E-01 3.2674900891332026E-01 3.2903955261110440E-01 3.3085644868674946E-01 3.3221180222315250E-01 3.3311819183781749E-01 3.3358861551336028E-01 3.3363643747226646E-01 3.3327533644680479E-01 3.3251925574618535E-01 3.3138235555063661E-01 3.2987896785765541E-01 3.2802355446432063E-01 3.2583066829125656E-01 3.2331491824388092E-01 3.2049093767517822E-01 3.1737335637490266E-01 3.1397677587752010E-01 3.1031574776877768E-01 3.0640475458865390E-01 3.0225819288209277E-01 2.9789035793884733E-01 2.9331542978613401E-01 2.8854746004555132E-01 2.8360035933025424E-01 2.7848788493091414E-01 2.7322362861181038E-01 2.6782100440545958E-01 2.6229323635149782E-01 2.5665334617090890E-01 2.5091414089963454E-01 2.4508820052662295E-01 2.3918786569184444E-01 2.3322522550138167E-01 2.2721210551125876E-01 2.2116005592100937E-01 2.1508034000383511E-01 2.0898392278423666E-01 2.0288145995773893E-01 1.9678328703236839E-01 1.9069940865933635E-01 1.8463948811246558E-01 1.7861283687365942E-01 1.7262840428640916E-01 1.6669476725188756E-01 1.6082011996305803E-01 1.5501226370124838E-01 1.4927859675583047E-01 1.4362610456919694E-01 1.3806135025345842E-01 1.3259046566885269E-01 1.2721914329298040E-01 1.2195262914082398E-01 1.1679571701460324E-01 1.1175274436715386E-01 1.0682759005485028E-01 1.0202367419350118E-01 9.7343960412273056E-02 9.2790960527516578E-02 8.8366741798533668E-02 8.4072936757633110E-02 7.9910755555189061E-02 7.5881000690994252E-02 7.1984083939820268E-02 6.8220045224105200E-02 6.4588573141972749E-02 6.1089026825455452E-02 5.7720458782234974E-02 5.4481638364290416E-02 5.1371075508013925E-02 4.8387044401803199E-02 4.5527606757915930E-02 4.2790634394426479E-02 4.0173830869361903E-02 3.7674751951324345E-02 3.5290824757849108E-02 3.3019365442927294E-02 3.0857595366888702E-02 2.8802655733324873E-02 2.6851620726915743E-02 2.5001509230826464E-02 2.3249295240776877E-02 2.1591917123224849E-02 2.0026285886065635E-02 1.8549292641124402E-02 1.7157815438481099E-02 1.5848725643968494E-02 1.4618894014295574E-02 1.3465196600921801E-02 1.2384520586092275E-02 1.1373770124489152E-02 1.0429872233812761E-02 9.5497827490838745E-03 8.7304923299969788E-03 7.9690324892796732E-03 7.2624815933254767E-03 6.6079707745730137E-03 6.0026896880791695E-03 5.4438920420952688E-03 4.9289008336450314E-03 4.4551132244576895E-03 4.0200049994303126E-03 3.6211345583893168E-03 3.2561464016543158E-03 2.9227740802105491E-03 2.6188425916892563E-03 2.3422702134487483E-03 2.0910697735406557E-03 1.8633493690162835E-03 1.6573125487287610E-03 1.4712579844325892E-03 1.3035786595375549E-03 1.1527606093453872E-03 1.0173812500219859E-03 8.9610733599635177E-04 7.8769258700617055E-04 6.9097502671640820E-04 6.0487407481398696E-04 5.2838743382286647E-04 4.6058781068325933E-04 4.0061951148616121E-04 3.4769494573531526E-04 3.0109107420260469E-04 2.6014583192262821E-04 2.2425455520395522E-04 1.9286643877736002E-04 1.6548104640738543E-04 1.4164489550825459E-04 1.2094813356748020E-04 1.0302132152333212E-04 8.7532336692859074E-05 7.4183405427334558E-05 6.2708273398940311E-05 5.2869519308951437E-05 4.4456015862464570E-05 3.7280540083094684E-05 3.1177533445281915E-05 2.6001010881371668E-05 2.1622616472633091E-05 1.7929822553039333E-05 1.4824268035468360E-05 1.2220231004165591E-05 1.0043229995931736E-05 8.2287479058370626E-06 6.7210720910029811E-06 5.4722439974488548E-06 4.4411114892981363E-06 3.5924770058790904E-06 2.8963346996725618E-06 2.3271898061387470E-06 1.8634536550483577E-06 1.4869079423595707E-06 1.1822321327635294E-06 9.3658814720380613E-07 7.3925679903639325E-07 5.8132076978518049E-07 4.5538925410537450E-07 3.5535974773596370E-07 2.7621279674243077E-07 2.1383586674864311E-07 1.6487282332388779E-07 1.2659583605616873E-07 9.6796826537843456E-08 7.3695872509245048E-08 5.5864255264097145E-08 4.2160094103718157E-08 3.1674749545121328E-08 2.3688395924763672E-08 1.7633364102361245E-08 1.3064036540298078E-08 9.6322407238089783E-09 7.0672334881468878E-09 5.1594992649435302E-09 3.7477005866401798E-09 2.7082204981341288E-09 1.9468249578378238E-09 1.3920500147035221E-09 9.8998465842184052E-10 7.0017685952206076E-10 4.9243849950603674E-10 3.4436563434553601E-10 2.3942476615349563E-10 1.6548437327765001E-10 1.1369464849273210E-10 7.7637922136078195E-11 5.2688230596248032E-11 3.5531486734890130E-11 2.3808205142361002E-11 1.5849155074754250E-11 1.0481022047140694E-11 6.8844664381445676E-12 4.4911372296973634E-12 2.9094518322136904E-12 1.8714723032979784E-12 1.1951454053243829E-12 7.5765248562285085E-13 4.7673528499963370E-13 2.9770598192030993E-13 1.8447818674255487E-13 1.1342085992562773E-13 6.9178897011580950E-14 4.1853183876312442E-14 2.5112963970272436E-14 1.4942439906838269E-14 8.8153107445194858E-15 5.1556544449551225E-15 2.9887978923196486E-15 1.7171623672041502E-15 9.7760343294542728E-16 5.5142196565210352E-16 3.0811142435893177E-16 1.7051606307043215E-16 9.3451623943890151E-17 5.0710945837924440E-17 2.7241940768877427E-17 1.4485148456133860E-17 7.6222369812450722E-18 3.9686378286809369E-18 2.0442022351693860E-18 1.0414834631279123E-18 5.2474546701897406E-19 2.6141673748551630E-19 1.2874369147783984E-19 6.2667852445615288E-20 3.0144443544291301E-20 1.4326152742270650E-20 6.7255407736987027E-21 3.1182738738483828E-21 1.4275789982111237E-21 6.4521245900294620E-22 2.8785350009868795E-22 1.2668387389536299E-22 5.4883665370279662E-23 2.3448065376216967E-23 9.8766567956686899E-24 4.1005970424080459E-24 </ae_partial_wave> <pseudo_partial_wave state= "Ni1" grid="log1"> 3.8731115022111479E-01 3.8731115022117202E-01 3.8731115022134832E-01 3.8731115022164952E-01 3.8731115022208196E-01 3.8731115022265222E-01 3.8731115022336698E-01 3.8731115022423357E-01 3.8731115022525908E-01 3.8731115022645141E-01 3.8731115022781842E-01 3.8731115022936835E-01 3.8731115023110979E-01 3.8731115023305185E-01 3.8731115023520363E-01 3.8731115023757484E-01 3.8731115024017537E-01 3.8731115024301593E-01 3.8731115024610685E-01 3.8731115024945961E-01 3.8731115025308582E-01 3.8731115025699758E-01 3.8731115026120744E-01 3.8731115026572838E-01 3.8731115027057395E-01 3.8731115027575808E-01 3.8731115028129542E-01 3.8731115028720092E-01 3.8731115029349045E-01 3.8731115030018032E-01 3.8731115030728736E-01 3.8731115031482888E-01 3.8731115032282309E-01 3.8731115033128899E-01 3.8731115034024610E-01 3.8731115034971458E-01 3.8731115035971558E-01 3.8731115037027075E-01 3.8731115038140290E-01 3.8731115039313535E-01 3.8731115040549247E-01 3.8731115041849945E-01 3.8731115043218245E-01 3.8731115044656861E-01 3.8731115046168607E-01 3.8731115047756376E-01 3.8731115049423231E-01 3.8731115051172249E-01 3.8731115053006721E-01 3.8731115054929993E-01 3.8731115056945559E-01 3.8731115059057025E-01 3.8731115061268134E-01 3.8731115063582799E-01 3.8731115066005012E-01 3.8731115068538957E-01 3.8731115071188954E-01 3.8731115073959477E-01 3.8731115076855177E-01 3.8731115079880846E-01 3.8731115083041479E-01 3.8731115086342227E-01 3.8731115089788465E-01 3.8731115093385693E-01 3.8731115097139673E-01 3.8731115101056346E-01 3.8731115105141883E-01 3.8731115109402664E-01 3.8731115113845288E-01 3.8731115118476600E-01 3.8731115123303705E-01 3.8731115128333932E-01 3.8731115133574912E-01 3.8731115139034522E-01 3.8731115144720907E-01 3.8731115150642542E-01 3.8731115156808171E-01 3.8731115163226870E-01 3.8731115169908015E-01 3.8731115176861347E-01 3.8731115184096920E-01 3.8731115191625176E-01 3.8731115199456911E-01 3.8731115207603295E-01 3.8731115216075923E-01 3.8731115224886775E-01 3.8731115234048286E-01 3.8731115243573272E-01 3.8731115253475079E-01 3.8731115263767457E-01 3.8731115274464700E-01 3.8731115285581552E-01 3.8731115297133328E-01 3.8731115309135855E-01 3.8731115321605508E-01 3.8731115334559285E-01 3.8731115348014722E-01 3.8731115361990021E-01 3.8731115376504022E-01 3.8731115391576176E-01 3.8731115407226691E-01 3.8731115423476425E-01 3.8731115440347014E-01 3.8731115457860832E-01 3.8731115476041034E-01 3.8731115494911600E-01 3.8731115514497344E-01 3.8731115534823934E-01 3.8731115555917983E-01 3.8731115577807007E-01 3.8731115600519461E-01 3.8731115624084850E-01 3.8731115648533665E-01 3.8731115673897493E-01 3.8731115700209001E-01 3.8731115727502030E-01 3.8731115755811568E-01 3.8731115785173853E-01 3.8731115815626349E-01 3.8731115847207892E-01 3.8731115879958600E-01 3.8731115913920056E-01 3.8731115949135236E-01 3.8731115985648645E-01 3.8731116023506346E-01 3.8731116062755949E-01 3.8731116103446811E-01 3.8731116145629929E-01 3.8731116189358111E-01 3.8731116234685981E-01 3.8731116281670086E-01 3.8731116330368920E-01 3.8731116380843000E-01 3.8731116433154977E-01 3.8731116487369655E-01 3.8731116543554067E-01 3.8731116601777593E-01 3.8731116662112025E-01 3.8731116724631631E-01 3.8731116789413256E-01 3.8731116856536407E-01 3.8731116926083337E-01 3.8731116998139142E-01 3.8731117072791893E-01 3.8731117150132655E-01 3.8731117230255691E-01 3.8731117313258462E-01 3.8731117399241882E-01 3.8731117488310279E-01 3.8731117580571606E-01 3.8731117676137544E-01 3.8731117775123619E-01 3.8731117877649335E-01 3.8731117983838337E-01 3.8731118093818506E-01 3.8731118207722143E-01 3.8731118325686104E-01 3.8731118447851942E-01 3.8731118574366091E-01 3.8731118705380008E-01 3.8731118841050377E-01 3.8731118981539236E-01 3.8731119127014219E-01 3.8731119277648696E-01 3.8731119433621974E-01 3.8731119595119545E-01 3.8731119762333199E-01 3.8731119935461372E-01 3.8731120114709255E-01 3.8731120300289040E-01 3.8731120492420240E-01 3.8731120691329818E-01 3.8731120897252513E-01 3.8731121110431094E-01 3.8731121331116602E-01 3.8731121559568649E-01 3.8731121796055695E-01 3.8731122040855354E-01 3.8731122294254694E-01 3.8731122556550546E-01 3.8731122828049847E-01 3.8731123109069970E-01 3.8731123399939055E-01 3.8731123700996384E-01 3.8731124012592744E-01 3.8731124335090839E-01 3.8731124668865607E-01 3.8731125014304735E-01 3.8731125371808955E-01 3.8731125741792599E-01 3.8731126124683929E-01 3.8731126520925702E-01 3.8731126930975557E-01 3.8731127355306549E-01 3.8731127794407638E-01 3.8731128248784241E-01 3.8731128718958696E-01 3.8731129205470871E-01 3.8731129708878714E-01 3.8731130229758837E-01 3.8731130768707112E-01 3.8731131326339296E-01 3.8731131903291671E-01 3.8731132500221693E-01 3.8731133117808653E-01 3.8731133756754393E-01 3.8731134417784052E-01 3.8731135101646735E-01 3.8731135809116291E-01 3.8731136540992089E-01 3.8731137298099855E-01 3.8731138081292432E-01 3.8731138891450639E-01 3.8731139729484149E-01 3.8731140596332408E-01 3.8731141492965443E-01 3.8731142420384901E-01 3.8731143379624944E-01 3.8731144371753257E-01 3.8731145397872035E-01 3.8731146459119020E-01 3.8731147556668566E-01 3.8731148691732670E-01 3.8731149865562153E-01 3.8731151079447679E-01 3.8731152334721031E-01 3.8731153632756149E-01 3.8731154974970439E-01 3.8731156362825947E-01 3.8731157797830579E-01 3.8731159281539396E-01 3.8731160815555937E-01 3.8731162401533420E-01 3.8731164041176169E-01 3.8731165736240947E-01 3.8731167488538248E-01 3.8731169299933771E-01 3.8731171172349749E-01 3.8731173107766381E-01 3.8731175108223254E-01 3.8731177175820775E-01 3.8731179312721570E-01 3.8731181521151947E-01 3.8731183803403335E-01 3.8731186161833703E-01 3.8731188598869015E-01 3.8731191117004571E-01 3.8731193718806500E-01 3.8731196406913077E-01 3.8731199184036080E-01 3.8731202052962138E-01 3.8731205016553949E-01 3.8731208077751617E-01 3.8731211239573682E-01 3.8731214505118405E-01 3.8731217877564672E-01 3.8731221360172985E-01 3.8731224956286397E-01 3.8731228669331191E-01 3.8731232502817586E-01 3.8731236460340163E-01 3.8731240545578322E-01 3.8731244762296391E-01 3.8731249114343685E-01 3.8731253605654326E-01 3.8731258240246758E-01 3.8731263022223167E-01 3.8731267955768500E-01 3.8731273045149206E-01 3.8731278294711774E-01 3.8731283708880704E-01 3.8731289292156251E-01 3.8731295049111675E-01 3.8731300984390055E-01 3.8731307102700557E-01 3.8731313408814178E-01 3.8731319907558848E-01 3.8731326603813909E-01 3.8731333502503923E-01 3.8731340608591608E-01 3.8731347927069998E-01 3.8731355462953704E-01 3.8731363221269127E-01 3.8731371207043741E-01 3.8731379425293994E-01 3.8731387881012219E-01 3.8731396579152000E-01 3.8731405524612200E-01 3.8731414722219376E-01 3.8731424176708401E-01 3.8731433892701467E-01 3.8731443874684918E-01 3.8731454126984022E-01 3.8731464653735426E-01 3.8731475458857184E-01 3.8731486546016064E-01 3.8731497918592001E-01 3.8731509579639389E-01 3.8731521531845203E-01 3.8731533777483368E-01 3.8731546318365345E-01 3.8731559155786610E-01 3.8731572290468547E-01 3.8731585722495704E-01 3.8731599451247789E-01 3.8731613475326110E-01 3.8731627792474188E-01 3.8731642399491845E-01 3.8731657292142524E-01 3.8731672465053157E-01 3.8731687911606177E-01 3.8731703623823038E-01 3.8731719592238567E-01 3.8731735805765560E-01 3.8731752251548907E-01 3.8731768914808412E-01 3.8731785778669542E-01 3.8731802823981287E-01 3.8731820029119962E-01 3.8731837369778344E-01 3.8731854818738631E-01 3.8731872345628410E-01 3.8731889916658246E-01 3.8731907494339562E-01 3.8731925037181569E-01 3.8731942499365440E-01 3.8731959830394525E-01 3.8731976974718457E-01 3.8731993871329673E-01 3.8732010453330079E-01 3.8732026647466067E-01 3.8732042373629288E-01 3.8732057544321041E-01 3.8732072064077677E-01 3.8732085828854002E-01 3.8732098725362246E-01 3.8732110630362843E-01 3.8732121409904219E-01 3.8732130918507623E-01 3.8732138998293425E-01 3.8732145478044550E-01 3.8732150172202917E-01 3.8732152879793985E-01 3.8732153383274687E-01 3.8732151447299129E-01 3.8732146817396568E-01 3.8732139218555567E-01 3.8732128353707806E-01 3.8732113902104670E-01 3.8732095517579157E-01 3.8732072826685415E-01 3.8732045426707196E-01 3.8732012883526629E-01 3.8731974729343432E-01 3.8731930460234570E-01 3.8731879533543351E-01 3.8731821365086472E-01 3.8731755326166545E-01 3.8731680740377011E-01 3.8731596880185337E-01 3.8731502963279535E-01 3.8731398148662183E-01 3.8731281532474660E-01 3.8731152143533892E-01 3.8731008938562067E-01 3.8730850797088895E-01 3.8730676516004631E-01 3.8730484803740589E-01 3.8730274274052534E-01 3.8730043439380385E-01 3.8729790703756739E-01 3.8729514355234129E-01 3.8729212557799508E-01 3.8728883342742632E-01 3.8728524599442310E-01 3.8728134065533065E-01 3.8727709316411729E-01 3.8727247754041438E-01 3.8726746595007794E-01 3.8726202857779130E-01 3.8725613349119958E-01 3.8724974649603955E-01 3.8724283098168821E-01 3.8723534775653079E-01 3.8722725487250365E-01 3.8721850743813591E-01 3.8720905741937373E-01 3.8719885342742766E-01 3.8718784049284666E-01 3.8717595982496766E-01 3.8716314855585504E-01 3.8714933946778557E-01 3.8713446070328827E-01 3.8711843545669544E-01 3.8710118164610452E-01 3.8708261156459711E-01 3.8706263150949516E-01 3.8704114138838408E-01 3.8701803430055959E-01 3.8699319609249661E-01 3.8696650488587125E-01 3.8693783057659620E-01 3.8690703430326534E-01 3.8687396788333006E-01 3.8683847321525938E-01 3.8680038164486547E-01 3.8675951329390279E-01 3.8671567634897985E-01 3.8666866630875069E-01 3.8661826518728348E-01 3.8656424067143846E-01 3.8650634523002181E-01 3.8644431517241890E-01 3.8637786965436199E-01 3.8630670962842567E-01 3.8623051673680969E-01 3.8614895214392786E-01 3.8606165530629738E-01 3.8596824267720914E-01 3.8586830634365837E-01 3.8576141259302699E-01 3.8564710040704542E-01 3.8552487988060885E-01 3.8539423056310090E-01 3.8525459971997583E-01 3.8510540051248149E-01 3.8494601009356982E-01 3.8477576761823340E-01 3.8459397216675784E-01 3.8439988057965147E-01 3.8419270520336435E-01 3.8397161154628634E-01 3.8373571584497629E-01 3.8348408254108968E-01 3.8321572167006873E-01 3.8292958616333178E-01 3.8262456906646503E-01 3.8229950067677509E-01 3.8195314560452498E-01 3.8158419976325186E-01 3.8119128729575830E-01 3.8077295744369488E-01 3.8032768137011347E-01 3.7985384894598573E-01 3.7934976551344296E-01 3.7881364864043227E-01 3.7824362488358926E-01 3.7763772657841538E-01 3.7699388867833417E-01 3.7630994566686898E-01 3.7558362857007027E-01 3.7481256209939934E-01 3.7399426195857027E-01 3.7312613235134612E-01 3.7220546373099372E-01 3.7122943083599386E-01 3.7019509106069742E-01 3.6909938321386970E-01 3.6793912672247836E-01 3.6671102134261518E-01 3.6541164744406479E-01 3.6403746693971079E-01 3.6258482493564226E-01 3.6104995218244457E-01 3.5942896841262961E-01 3.5771788665343707E-01 3.5591261860818579E-01 3.5400898120288421E-01 3.5200270439778986E-01 3.4988944036588265E-01 3.4766477414165031E-01 3.4532423584395949E-01 3.4286331457594688E-01 3.4027747410254733E-01 3.3756217040227715E-01 3.3471287118393550E-01 3.3172507745070173E-01 3.2859434718340302E-01 3.2531632120119885E-01 3.2188675124126093E-01 3.1830153027889924E-01 3.1455672508568538E-01 3.1064861099512336E-01 3.0657370881305596E-01 3.0232882377298226E-01 2.9791108639458680E-01 2.9331799505690420E-01 2.8854746004555132E-01 2.8360035933025424E-01 2.7848788493091414E-01 2.7322362861181038E-01 2.6782100440545958E-01 2.6229323635149782E-01 2.5665334617090890E-01 2.5091414089963454E-01 2.4508820052662295E-01 2.3918786569184444E-01 2.3322522550138167E-01 2.2721210551125876E-01 2.2116005592100937E-01 2.1508034000383511E-01 2.0898392278423666E-01 2.0288145995773893E-01 1.9678328703236839E-01 1.9069940865933635E-01 1.8463948811246558E-01 1.7861283687365942E-01 1.7262840428640916E-01 1.6669476725188756E-01 1.6082011996305803E-01 1.5501226370124838E-01 1.4927859675583047E-01 1.4362610456919694E-01 1.3806135025345842E-01 1.3259046566885269E-01 1.2721914329298040E-01 1.2195262914082398E-01 1.1679571701460324E-01 1.1175274436715386E-01 1.0682759005485028E-01 1.0202367419350118E-01 9.7343960412273056E-02 9.2790960527516578E-02 8.8366741798533668E-02 8.4072936757633110E-02 7.9910755555189061E-02 7.5881000690994252E-02 7.1984083939820268E-02 6.8220045224105200E-02 6.4588573141972749E-02 6.1089026825455452E-02 5.7720458782234974E-02 5.4481638364290416E-02 5.1371075508013925E-02 4.8387044401803199E-02 4.5527606757915930E-02 4.2790634394426479E-02 4.0173830869361903E-02 3.7674751951324345E-02 3.5290824757849108E-02 3.3019365442927294E-02 3.0857595366888702E-02 2.8802655733324873E-02 2.6851620726915743E-02 2.5001509230826464E-02 2.3249295240776877E-02 2.1591917123224849E-02 2.0026285886065635E-02 1.8549292641124402E-02 1.7157815438481099E-02 1.5848725643968494E-02 1.4618894014295574E-02 1.3465196600921801E-02 1.2384520586092275E-02 1.1373770124489152E-02 1.0429872233812761E-02 9.5497827490838745E-03 8.7304923299969788E-03 7.9690324892796732E-03 7.2624815933254767E-03 6.6079707745730137E-03 6.0026896880791695E-03 5.4438920420952688E-03 4.9289008336450314E-03 4.4551132244576895E-03 4.0200049994303126E-03 3.6211345583893168E-03 3.2561464016543158E-03 2.9227740802105491E-03 2.6188425916892563E-03 2.3422702134487483E-03 2.0910697735406557E-03 1.8633493690162835E-03 1.6573125487287610E-03 1.4712579844325892E-03 1.3035786595375549E-03 1.1527606093453872E-03 1.0173812500219859E-03 8.9610733599635177E-04 7.8769258700617055E-04 6.9097502671640820E-04 6.0487407481398696E-04 5.2838743382286647E-04 4.6058781068325933E-04 4.0061951148616121E-04 3.4769494573531526E-04 3.0109107420260469E-04 2.6014583192262821E-04 2.2425455520395522E-04 1.9286643877736002E-04 1.6548104640738543E-04 1.4164489550825459E-04 1.2094813356748020E-04 1.0302132152333212E-04 8.7532336692859074E-05 7.4183405427334558E-05 6.2708273398940311E-05 5.2869519308951437E-05 4.4456015862464570E-05 3.7280540083094684E-05 3.1177533445281915E-05 2.6001010881371668E-05 2.1622616472633091E-05 1.7929822553039333E-05 1.4824268035468360E-05 1.2220231004165591E-05 1.0043229995931736E-05 8.2287479058370626E-06 6.7210720910029811E-06 5.4722439974488548E-06 4.4411114892981363E-06 3.5924770058790904E-06 2.8963346996725618E-06 2.3271898061387470E-06 1.8634536550483577E-06 1.4869079423595707E-06 1.1822321327635294E-06 9.3658814720380613E-07 7.3925679903639325E-07 5.8132076978518049E-07 4.5538925410537450E-07 3.5535974773596370E-07 2.7621279674243077E-07 2.1383586674864311E-07 1.6487282332388779E-07 1.2659583605616873E-07 9.6796826537843456E-08 7.3695872509245048E-08 5.5864255264097145E-08 4.2160094103718157E-08 3.1674749545121328E-08 2.3688395924763672E-08 1.7633364102361245E-08 1.3064036540298078E-08 9.6322407238089783E-09 7.0672334881468878E-09 5.1594992649435302E-09 3.7477005866401798E-09 2.7082204981341288E-09 1.9468249578378238E-09 1.3920500147035221E-09 9.8998465842184052E-10 7.0017685952206076E-10 4.9243849950603674E-10 3.4436563434553601E-10 2.3942476615349563E-10 1.6548437327765001E-10 1.1369464849273210E-10 7.7637922136078195E-11 5.2688230596248032E-11 3.5531486734890130E-11 2.3808205142361002E-11 1.5849155074754250E-11 1.0481022047140694E-11 6.8844664381445676E-12 4.4911372296973634E-12 2.9094518322136904E-12 1.8714723032979784E-12 1.1951454053243829E-12 7.5765248562285085E-13 4.7673528499963370E-13 2.9770598192030993E-13 1.8447818674255487E-13 1.1342085992562773E-13 6.9178897011580950E-14 4.1853183876312442E-14 2.5112963970272436E-14 1.4942439906838269E-14 8.8153107445194858E-15 5.1556544449551225E-15 2.9887978923196486E-15 1.7171623672041502E-15 9.7760343294542728E-16 5.5142196565210352E-16 3.0811142435893177E-16 1.7051606307043215E-16 9.3451623943890151E-17 5.0710945837924440E-17 2.7241940768877427E-17 1.4485148456133860E-17 7.6222369812450722E-18 3.9686378286809369E-18 2.0442022351693860E-18 1.0414834631279123E-18 5.2474546701897406E-19 2.6141673748551630E-19 1.2874369147783984E-19 6.2667852445615288E-20 3.0144443544291301E-20 1.4326152742270650E-20 6.7255407736987027E-21 3.1182738738483828E-21 1.4275789982111237E-21 6.4521245900294620E-22 2.8785350009868795E-22 1.2668387389536299E-22 5.4883665370279662E-23 2.3448065376216967E-23 9.8766567956686899E-24 4.1005970424080459E-24 </pseudo_partial_wave> <projector_function state= "Ni1" grid="log1"> 3.2174644372690202E+00 3.2174644372508014E+00 3.2174644371948551E+00 3.2174644370992684E+00 3.2174644369620409E+00 3.2174644367810905E+00 3.2174644365542489E+00 3.2174644362792697E+00 3.2174644359538105E+00 3.2174644355754412E+00 3.2174644351416362E+00 3.2174644346497683E+00 3.2174644340971108E+00 3.2174644334808313E+00 3.2174644327979807E+00 3.2174644320455057E+00 3.2174644312202294E+00 3.2174644303188535E+00 3.2174644293379493E+00 3.2174644282739635E+00 3.2174644271232018E+00 3.2174644258818312E+00 3.2174644245458719E+00 3.2174644231111893E+00 3.2174644215734971E+00 3.2174644199283442E+00 3.2174644181711098E+00 3.2174644162970032E+00 3.2174644143010447E+00 3.2174644121780798E+00 3.2174644099227465E+00 3.2174644075294925E+00 3.2174644049925507E+00 3.2174644023059424E+00 3.2174643994634669E+00 3.2174643964586869E+00 3.2174643932849309E+00 3.2174643899352784E+00 3.2174643864025527E+00 3.2174643826793079E+00 3.2174643787578265E+00 3.2174643746301066E+00 3.2174643702878472E+00 3.2174643657224440E+00 3.2174643609249753E+00 3.2174643558861939E+00 3.2174643505965133E+00 3.2174643450459897E+00 3.2174643392243238E+00 3.2174643331208346E+00 3.2174643267244516E+00 3.2174643200237023E+00 3.2174643130066936E+00 3.2174643056611041E+00 3.2174642979741574E+00 3.2174642899326202E+00 3.2174642815227750E+00 3.2174642727304081E+00 3.2174642635407897E+00 3.2174642539386586E+00 3.2174642439082048E+00 3.2174642334330410E+00 3.2174642224961958E+00 3.2174642110800784E+00 3.2174641991664710E+00 3.2174641867364975E+00 3.2174641737706042E+00 3.2174641602485319E+00 3.2174641461492999E+00 3.2174641314511669E+00 3.2174641161316226E+00 3.2174641001673390E+00 3.2174640835341659E+00 3.2174640662070817E+00 3.2174640481601684E+00 3.2174640293665897E+00 3.2174640097985483E+00 3.2174639894272530E+00 3.2174639682228880E+00 3.2174639461545835E+00 3.2174639231903570E+00 3.2174638992970994E+00 3.2174638744405226E+00 3.2174638485851146E+00 3.2174638216941105E+00 3.2174637937294350E+00 3.2174637646516664E+00 3.2174637344199812E+00 3.2174637029921178E+00 3.2174636703243085E+00 3.2174636363712423E+00 3.2174636010860045E+00 3.2174635644200240E+00 3.2174635263230087E+00 3.2174634867428940E+00 3.2174634456257785E+00 3.2174634029158531E+00 3.2174633585553485E+00 3.2174633124844525E+00 3.2174632646412475E+00 3.2174632149616356E+00 3.2174631633792612E+00 3.2174631098254358E+00 3.2174630542290479E+00 3.2174629965164963E+00 3.2174629366115828E+00 3.2174628744354368E+00 3.2174628099064155E+00 3.2174627429400093E+00 3.2174626734487441E+00 3.2174626013420773E+00 3.2174625265262859E+00 3.2174624489043664E+00 3.2174623683759100E+00 3.2174622848369929E+00 3.2174621981800486E+00 3.2174621082937449E+00 3.2174620150628543E+00 3.2174619183681106E+00 3.2174618180860781E+00 3.2174617140890054E+00 3.2174616062446706E+00 3.2174614944162276E+00 3.2174613784620525E+00 3.2174612582355682E+00 3.2174611335850773E+00 3.2174610043535883E+00 3.2174608703786198E+00 3.2174607314920274E+00 3.2174605875197910E+00 3.2174604382818219E+00 3.2174602835917456E+00 3.2174601232566866E+00 3.2174599570770464E+00 3.2174597848462620E+00 3.2174596063505732E+00 3.2174594213687655E+00 3.2174592296719156E+00 3.2174590310231257E+00 3.2174588251772431E+00 3.2174586118805730E+00 3.2174583908705903E+00 3.2174581618756202E+00 3.2174579246145356E+00 3.2174576787964138E+00 3.2174574241202105E+00 3.2174571602743987E+00 3.2174568869366138E+00 3.2174566037732673E+00 3.2174563104391645E+00 3.2174560065771014E+00 3.2174556918174422E+00 3.2174553657776919E+00 3.2174550280620551E+00 3.2174546782609599E+00 3.2174543159505937E+00 3.2174539406924034E+00 3.2174535520325755E+00 3.2174531495015199E+00 3.2174527326133093E+00 3.2174523008651232E+00 3.2174518537366441E+00 3.2174513906894675E+00 3.2174509111664547E+00 3.2174504145910987E+00 3.2174499003668369E+00 3.2174493678763558E+00 3.2174488164808732E+00 3.2174482455193862E+00 3.2174476543078963E+00 3.2174470421386112E+00 3.2174464082791103E+00 3.2174457519714919E+00 3.2174450724314796E+00 3.2174443688475036E+00 3.2174436403797468E+00 3.2174428861591600E+00 3.2174421052864348E+00 3.2174412968309518E+00 3.2174404598296849E+00 3.2174395932860631E+00 3.2174386961687995E+00 3.2174377674106740E+00 3.2174368059072718E+00 3.2174358105156844E+00 3.2174347800531558E+00 3.2174337132956823E+00 3.2174326089765635E+00 3.2174314657849030E+00 3.2174302823640568E+00 3.2174290573100128E+00 3.2174277891697347E+00 3.2174264764394263E+00 3.2174251175627426E+00 3.2174237109289332E+00 3.2174222548709239E+00 3.2174207476633181E+00 3.2174191875203406E+00 3.2174175725936949E+00 3.2174159009703427E+00 3.2174141706702128E+00 3.2174123796438128E+00 3.2174105257697669E+00 3.2174086068522505E+00 3.2174066206183416E+00 3.2174045647152649E+00 3.2174024367075473E+00 3.2174002340740508E+00 3.2173979542049107E+00 3.2173955943983503E+00 3.2173931518573875E+00 3.2173906236864074E+00 3.2173880068876071E+00 3.2173852983573177E+00 3.2173824948821870E+00 3.2173795931351958E+00 3.2173765896715607E+00 3.2173734809244450E+00 3.2173702632005354E+00 3.2173669326754299E+00 3.2173634853888626E+00 3.2173599172397394E+00 3.2173562239809788E+00 3.2173524012141619E+00 3.2173484443839739E+00 3.2173443487724223E+00 3.2173401094928353E+00 3.2173357214836251E+00 3.2173311795018105E+00 3.2173264781162669E+00 3.2173216117007319E+00 3.2173165744265226E+00 3.2173113602549566E+00 3.2173059629294785E+00 3.2173003759674685E+00 3.2172945926517151E+00 3.2172886060215511E+00 3.2172824088636176E+00 3.2172759937022626E+00 3.2172693527895291E+00 3.2172624780947587E+00 3.2172553612937214E+00 3.2172479937573364E+00 3.2172403665398943E+00 3.2172324703667954E+00 3.2172242956217647E+00 3.2172158323335225E+00 3.2172070701619013E+00 3.2171979983833490E+00 3.2171886058758159E+00 3.2171788811029902E+00 3.2171688120978423E+00 3.2171583864454538E+00 3.2171475912650780E+00 3.2171364131914353E+00 3.2171248383551458E+00 3.2171128523622956E+00 3.2171004402731085E+00 3.2170875865796167E+00 3.2170742751823438E+00 3.2170604893659074E+00 3.2170462117735155E+00 3.2170314243802571E+00 3.2170161084651867E+00 3.2170002445820756E+00 3.2169838125288015E+00 3.2169667913152815E+00 3.2169491591298955E+00 3.2169308933042831E+00 3.2169119702764717E+00 3.2168923655521895E+00 3.2168720536643258E+00 3.2168510081303907E+00 3.2168292014078861E+00 3.2168066048474651E+00 3.2167831886437628E+00 3.2167589217837635E+00 3.2167337719925593E+00 3.2167077056763902E+00 3.2166806878627470E+00 3.2166526821374357E+00 3.2166236505783892E+00 3.2165935536860526E+00 3.2165623503101606E+00 3.2165299975726538E+00 3.2164964507865768E+00 3.2164616633706542E+00 3.2164255867593492E+00 3.2163881703081141E+00 3.2163493611935228E+00 3.2163091043080687E+00 3.2162673421492025E+00 3.2162240147023513E+00 3.2161790593175317E+00 3.2161324105791502E+00 3.2160840001686375E+00 3.2160337567194266E+00 3.2159816056638557E+00 3.2159274690714899E+00 3.2158712654783450E+00 3.2158129097064516E+00 3.2157523126731982E+00 3.2156893811897862E+00 3.2156240177481852E+00 3.2155561202958216E+00 3.2154855819973114E+00 3.2154122909823863E+00 3.2153361300791921E+00 3.2152569765320593E+00 3.2151747017027481E+00 3.2150891707542035E+00 3.2150002423156865E+00 3.2149077681281431E+00 3.2148115926685956E+00 3.2147115527522234E+00 3.2146074771107731E+00 3.2144991859458072E+00 3.2143864904552251E+00 3.2142691923313853E+00 3.2141470832290775E+00 3.2140199442014259E+00 3.2138875451017657E+00 3.2137496439493272E+00 3.2136059862564972E+00 3.2134563043152529E+00 3.2133003164402054E+00 3.2131377261655758E+00 3.2129682213932038E+00 3.2127914734885605E+00 3.2126071363215298E+00 3.2124148452484995E+00 3.2122142160321601E+00 3.2120048436951079E+00 3.2117863013032055E+00 3.2115581386742909E+00 3.2113198810077082E+00 3.2110710274297167E+00 3.2108110494496653E+00 3.2105393893214358E+00 3.2102554583043728E+00 3.2099586348175753E+00 3.2096482624810916E+00 3.2093236480371203E+00 3.2089840591440533E+00 3.2086287220356318E+00 3.2082568190372172E+00 3.2078674859306080E+00 3.2074598091584368E+00 3.2070328228586926E+00 3.2065855057193486E+00 3.2061167776426429E+00 3.2056254962079169E+00 3.2051104529214220E+00 3.2045703692408769E+00 3.2040038923619756E+00 3.2034095907534055E+00 3.2027859494262927E+00 3.2021313649233765E+00 3.2014441400124758E+00 3.2007224780681898E+00 3.1999644771250511E+00 3.1991681235846672E+00 3.1983312855586736E+00 3.1974517058286462E+00 3.1965269944034045E+00 3.1955546206534717E+00 3.1945319050018113E+00 3.1934560101493084E+00 3.1923239318128749E+00 3.1911324889535027E+00 3.1898783134711288E+00 3.1885578393426939E+00 3.1871672911794708E+00 3.1857026721795356E+00 3.1841597514510247E+00 3.1825340506819670E+00 3.1808208301325647E+00 3.1790150739261862E+00 3.1771114746159315E+00 3.1751044170044214E+00 3.1729879611955698E+00 3.1707558248585310E+00 3.1684013646857530E+00 3.1659175570292830E+00 3.1632969777020588E+00 3.1605317809340785E+00 3.1576136774770442E+00 3.1545339118553941E+00 3.1512832387666587E+00 3.1478518986399120E+00 3.1442295923677204E+00 3.1404054552346250E+00 3.1363680300737915E+00 3.1321052396933293E+00 3.1276043586246525E+00 3.1228519842578453E+00 3.1178340074425783E+00 3.1125355826488432E+00 3.1069410977986984E+00 3.1010341438993869E+00 3.0947974846291437E+00 3.0882130260501253E+00 3.0812617866483514E+00 3.0739238679282583E+00 3.0661784258198881E+00 3.0580036431896147E+00 3.0493767037811335E+00 3.0402737679519829E+00 3.0306699506124635E+00 3.0205393018183391E+00 3.0098547905162829E+00 2.9985882919916071E+00 2.9867105796213216E+00 2.9741913215919369E+00 2.9609990833004045E+00 2.9471013362179646E+00 2.9324644740601187E+00 2.9170538371709434E+00 2.9008337460960014E+00 2.8837675453844955E+00 2.8658176587271376E+00 2.8469456566005835E+00 2.8271123376508345E+00 2.8062778251056120E+00 2.7844016795574524E+00 2.7614430295036074E+00 2.7373607210635047E+00 2.7121134883172684E+00 2.6856601457171014E+00 2.6579598040140819E+00 2.6289721111134612E+00 2.5986575192179222E+00 2.5669775795373386E+00 2.5338952657312475E+00 2.4993753271024981E+00 2.4633846723732855E+00 2.4258927846435676E+00 2.3868721678524927E+00 2.3462988247313787E+00 2.3041527658480527E+00 2.2604185488924191E+00 2.2150858468385031E+00 2.1681500430350185E+00 2.1196128506214049E+00 2.0694829529364762E+00 2.0177766607793362E+00 1.9645185814948256E+00 1.9097422938858251E+00 1.8534910219001219E+00 1.7958182988970750E+00 1.7367886130659032E+00 1.6764780232381784E+00 1.6149747329065105E+00 1.5523796087216186E+00 1.4888066280815271E+00 1.4243832386382969E+00 1.3592506106168896E+00 1.2935637607552770E+00 1.2274915244248727E+00 1.1612163500725652E+00 1.0949338875491650E+00 1.0288523391843216E+00 9.6319153969786619E-01 8.9818172831389542E-01 8.3406197394787773E-01 7.7107821234380913E-01 7.0948085294924734E-01 6.4952191369223145E-01 5.9145164442805187E-01 5.3551460565821474E-01 4.8194517947247917E-01 4.3096250612146608E-01 3.8276486411489885E-01 3.3752354650122418E-01 2.9537633353701820E-01 2.5642072500270746E-01 2.2070717670087719E-01 1.8823268773368354E-01 1.5893521006905612E-01 1.3268950092083723E-01 1.0930521164200388E-01 8.8528202691902730E-02 7.0046289585562374E-02 5.3500854682892611E-02 3.8505998110784853E-02 2.4677141632415075E-02 1.1671236641624288E-02 7.0808760749551552E-04 -2.8805953667164762E-04 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 </projector_function> <ae_partial_wave state= "Ni2" grid="log1"> 1.7896025332282221E+01 1.7514955738993574E+01 1.7263476430526545E+01 1.7126904799923036E+01 1.7041732506544164E+01 1.6895625476070236E+01 1.6827545873058455E+01 1.6774473661544356E+01 1.6722944213450596E+01 1.6675966004332750E+01 1.6632565432442412E+01 1.6592031538038277E+01 1.6553976887738429E+01 1.6518041150828441E+01 1.6483925526865693E+01 1.6451388247687120E+01 1.6420227763813013E+01 1.6390275136527062E+01 1.6361387648164946E+01 1.6333443684831675E+01 1.6306338817396817E+01 1.6279982730260638E+01 1.6254296786733480E+01 1.6229212088420244E+01 1.6204667914451473E+01 1.6180610456135057E+01 1.6156991783403512E+01 1.6133768994529522E+01 1.6110903511873531E+01 1.6088360494860055E+01 1.6066108347725990E+01 1.6044118304399596E+01 1.6022364076551870E+01 1.6000821553700394E+01 1.5979468546447118E+01 1.5958284565651477E+01 1.5937250631698745E+01 1.5916349109090566E+01 1.5895563562442758E+01 1.5874878630660026E+01 1.5854279916606480E+01 1.5833753890043061E+01 1.5813287801962488E+01 1.5792869608753627E+01 1.5772487904871419E+01 1.5752131862890627E+01 1.5731791179990863E+01 1.5711456030059249E+01 1.5691117020714662E+01 1.5670765154656172E+01 1.5650391794819340E+01 1.5629988632896405E+01 1.5609547660834229E+01 1.5589061144974625E+01 1.5568521602545065E+01 1.5547921780244348E+01 1.5527254634700014E+01 1.5506513314601111E+01 1.5485691144333963E+01 1.5464781608968028E+01 1.5443778340458357E+01 1.5422675104944151E+01 1.5401465791039165E+01 1.5380144399018883E+01 1.5358705030821298E+01 1.5337141880786826E+01 1.5315449227069392E+01 1.5293621423661163E+01 1.5271652892975178E+01 1.5249538118938686E+01 1.5227271640554550E+01 1.5204848045890577E+01 1.5182261966462692E+01 1.5159508071979294E+01 1.5136581065419504E+01 1.5113475678417435E+01 1.5090186666930990E+01 1.5066708807172766E+01 1.5043036891783867E+01 1.5019165726232959E+01 1.4995090125425138E+01 1.4970804910505741E+01 1.4946304905845576E+01 1.4921584936196401E+01 1.4896639824004312E+01 1.4871464386872596E+01 1.4846053435163848E+01 1.4820401769733632E+01 1.4794504179787110E+01 1.4768355440853489E+01 1.4741950312870721E+01 1.4715283538374143E+01 1.4688349840786096E+01 1.4661143922799129E+01 1.4633660464850509E+01 1.4605894123683338E+01 1.4577839530990397E+01 1.4549491292138248E+01 1.4520843984968247E+01 1.4491892158672615E+01 1.4462630332741959E+01 1.4433052995983653E+01 1.4403154605608274E+01 1.4372929586383369E+01 1.4342372329851985E+01 1.4311477193616552E+01 1.4280238500685289E+01 1.4248650538881764E+01 1.4216707560316351E+01 1.4184403780919055E+01 1.4151733380033546E+01 1.4118690500072594E+01 1.4085269246233878E+01 1.4051463686277408E+01 1.4017267850364215E+01 1.3982675730955952E+01 1.3947681282777655E+01 1.3912278422842082E+01 1.3876461030538016E+01 1.3840222947782529E+01 1.3803557979237508E+01 1.3766459892593012E+01 1.3728922418916746E+01 1.3690939253071740E+01 1.3652504054203559E+01 1.3613610446297999E+01 1.3574252018810201E+01 1.3534422327368235E+01 1.3494114894550723E+01 1.3453323210741599E+01 1.3412040735063433E+01 1.3370260896390098E+01 1.3327977094442042E+01 1.3285182700965857E+01 1.3241871060998697E+01 1.3198035494222019E+01 1.3153669296404365E+01 1.3108765740937221E+01 1.3063318080465358E+01 1.3017319548614140E+01 1.2970763361816386E+01 1.2923642721240936E+01 1.2875950814825790E+01 1.2827680819418031E+01 1.2778825903023789E+01 1.2729379227170297E+01 1.2679333949382800E+01 1.2628683225780152E+01 1.2577420213790269E+01 1.2525538074989827E+01 1.2473029978070523E+01 1.2419889101934702E+01 1.2366108638923814E+01 1.2311681798182670E+01 1.2256601809162145E+01 1.2200861925264391E+01 1.2144455427632581E+01 1.2087375629089276E+01 1.2029615878226283E+01 1.1971169563649251E+01 1.1912030118380297E+01 1.1852191024421472E+01 1.1791645817483220E+01 1.1730388091880421E+01 1.1668411505599181E+01 1.1605709785538018E+01 1.1542276732926508E+01 1.1478106228924437E+01 1.1413192240404673E+01 1.1347528825923421E+01 1.1281110141879546E+01 1.1213930448867803E+01 1.1145984118227453E+01 1.1077265638790282E+01 1.1007769623829709E+01 1.0937490818214789E+01 1.0866424105771438E+01 1.0794564516852446E+01 1.0721907236120638E+01 1.0648447610545574E+01 1.0574181157617275E+01 1.0499103573777939E+01 1.0423210743074623E+01 1.0346498746033451E+01 1.0268963868757789E+01 1.0190602612250752E+01 1.0111411701964055E+01 1.0031388097573423E+01 9.9505290029810762E+00 9.8688318765465510E+00 9.7862944415443121E+00 9.7029146968496534E+00 9.6186909278511514E+00 9.5336217175890727E+00 9.4477059581189344E+00 9.3609428620982129E+00 9.2733319745938854E+00 9.1848731851095327E+00 9.0955667398278344E+00 9.0054132540663758E+00 8.9144137249419639E+00 8.8225695442402561E+00 8.7298825114850356E+00 8.6363548472025258E+00 8.5419892063744225E+00 8.4467886920735129E+00 8.3507568692746261E+00 8.2538977788333536E+00 8.1562159516238673E+00 8.0577164228274736E+00 7.9584047463611203E+00 7.8582870094363395E+00 7.7573698472364665E+00 7.6556604577007636E+00 7.5531666164017581E+00 7.4498966915029126E+00 7.3458596587808414E+00 7.2410651166975697E+00 7.1355233015052573E+00 7.0292451023669420E+00 6.9222420764734691E+00 6.8145264641381518E+00 6.7061112038480903E+00 6.5970099472499717E+00 6.4872370740483412E+00 6.3768077067914017E+00 6.2657377255201530E+00 6.1540437822532352E+00 6.0417433152808897E+00 5.9288545632384677E+00 5.8153965789296365E+00 5.7013892428674664E+00 5.5868532765009160E+00 5.4718102550920875E+00 5.3562826202091465E+00 5.2402936917975742E+00 5.1238676797916991E+00 5.0070296952265156E+00 4.8898057608090184E+00 4.7722228209060091E+00 4.6543087509048959E+00 4.5360923659016912E+00 4.4176034286698567E+00 4.2988726568615849E+00 4.1799317293922353E+00 4.0608132919568778E+00 3.9415509616273043E+00 3.8221793304758322E+00 3.7027339681714571E+00 3.5832514234929937E+00 3.4637692247021210E+00 3.3443258787190411E+00 3.2249608690417535E+00 3.1057146523497927E+00 2.9866286537322675E+00 2.8677452604790803E+00 2.7491078143743426E+00 2.6307606024299788E+00 2.5127488459974594E+00 2.3951186881953297E+00 2.2779171795900424E+00 2.1611922620677482E+00 2.0449927508345107E+00 1.9293683144828346E+00 1.8143694530625003E+00 1.7000474740942497E+00 1.5864544664649074E+00 1.4736432721434014E+00 1.3616674556575923E+00 1.2505812712723847E+00 1.1404396278106179E+00 1.0312980510590743E+00 9.2321264370344835E-01 8.1624004273757289E-01 7.1043737429455489E-01 6.0586220585044592E-01 5.0257249575488039E-01 4.0062654004836196E-01 3.0008291653248270E-01 2.0100042606792809E-01 1.0343803108576687E-01 7.4547913104948214E-03 -8.6890203291286966E-02 -1.7953790230494471E-01 -2.7042936735341466E-01 -3.5950584720228335E-01 -4.4670885539143695E-01 -5.3198025028089313E-01 -6.1526231738226844E-01 -6.9649785383630780E-01 -7.7563025489319726E-01 -8.5260360225721676E-01 -9.2736275417204739E-01 -9.9985343714717845E-01 -1.0700223392586401E+00 -1.1378172049958868E+00 -1.2031869316682304E+00 -1.2660816674238642E+00 -1.3264529109690184E+00 -1.3842536130992211E+00 -1.4394382801661343E+00 -1.4919630795997179E+00 -1.5417859475849109E+00 -1.5888666989538252E+00 -1.6331671393000320E+00 -1.6746511792514267E+00 -1.7132849507559669E+00 -1.7490369251454123E+00 -1.7818780326520691E+00 -1.8117817829705749E+00 -1.8387243863891594E+00 -1.8626848749681577E+00 -1.8836452232219183E+00 -1.9015904677618489E+00 -1.9165088253800568E+00 -1.9283918090863803E+00 -1.9372343416496387E+00 -1.9430348662289387E+00 -1.9457954537087812E+00 -1.9455219063687039E+00 -1.9422238575269415E+00 -1.9359148667970802E+00 -1.9266125105927574E+00 -1.9143384675084447E+00 -1.8991185981983787E+00 -1.8809830193715895E+00 -1.8599661715196600E+00 -1.8361068799957236E+00 -1.8094484090673826E+00 -1.7800385085726331E+00 -1.7479294528154865E+00 -1.7131780713460332E+00 -1.6758457712782371E+00 -1.6359985508065882E+00 -1.5937070035905654E+00 -1.5490463136829473E+00 -1.5020962406850535E+00 -1.4529410948183432E+00 -1.4016697016085244E+00 -1.3483753558849854E+00 -1.2931557648055731E+00 -1.2361129796247299E+00 -1.1773533159316651E+00 -1.1169872620959014E+00 -1.0551293756690503E+00 -9.9189816750587845E-01 -9.2741597338409798E-01 -8.6180881292147715E-01 -7.9520623561153725E-01 -7.2774115382530735E-01 -6.5954966265686021E-01 -5.9077084652537526E-01 -5.2154657248582714E-01 -4.5202127024473154E-01 -3.8234169892629899E-01 -3.1265670068762358E-01 -2.4311694133815032E-01 -1.7387463817781293E-01 -1.0508327532814228E-01 -3.6897306889246508E-02 3.0528151689347846E-02 9.7037643587179465E-02 1.6247570146359178E-01 2.2668718867422416E-01 2.8951765032829058E-01 3.5081367365321203E-01 4.1042325712932820E-01 4.6819618784888622E-01 5.2398442652436483E-01 5.7764249949863722E-01 6.2902789696336614E-01 6.7800147633700636E-01 7.2442786935445469E-01 7.6817589085204585E-01 8.0911894649601401E-01 8.4713543584977979E-01 8.8210914632643622E-01 9.1392963293209850E-01 9.4249257855394786E-01 9.6770013019557077E-01 9.8946120827160100E-01 1.0076917889521750E+00 1.0223151634402743E+00 1.0332621824909434E+00 1.0404714986115933E+00 1.0438898210492062E+00 1.0434721985214734E+00 1.0391823405166356E+00 1.0309929795999446E+00 1.0188862659394311E+00 1.0028541744456485E+00 9.8289889848457890E-01 9.5903320470555897E-01 9.3128073077329876E-01 8.9967621846333012E-01 8.6426568443382767E-01 8.2510653706345138E-01 7.8226764945959060E-01 7.3582939734212660E-01 6.8588366776591303E-01 6.3253384188345074E-01 5.7589475279856073E-01 5.1609261816565521E-01 4.5326494646632565E-01 3.8756041569736582E-01 3.1913872338196619E-01 2.4817040723207143E-01 1.7483663632732677E-01 9.9328973237482424E-02 2.1849108027114105E-02 -5.7391434503377775E-02 -1.3817161269232134E-01 -2.2026120918888092E-01 -3.0342119354866037E-01 -3.8740410441846912E-01 -4.7195444959026150E-01 -5.5680912237341718E-01 -6.4169783294113036E-01 -7.2634355353770719E-01 -8.1046297667866141E-01 -8.9376698572742508E-01 -9.7596113748640534E-01 -1.0567461566917888E+00 -1.1358184425482631E+00 -1.2128705876790087E+00 -1.2875919100954374E+00 -1.3596689990081590E+00 -1.4287862755031711E+00 -1.4946265692932470E+00 -1.5568717129219722E+00 -1.6152031549454291E+00 -1.6693025937425776E+00 -1.7188526337093131E+00 -1.7635374656726770E+00 -1.8030435734207384E+00 -1.8370604682813401E+00 -1.8652814537001348E+00 -1.8874044217671506E+00 -1.9031326836232170E+00 -1.9121758356455809E+00 -1.9142506632677163E+00 -1.9090820842339664E+00 -1.8964041330260555E+00 -1.8759609881265631E+00 -1.8475080437034810E+00 -1.8108130272057348E+00 -1.7656571642514594E+00 -1.7118363920587378E+00 -1.6491626225054863E+00 -1.5774650557042202E+00 -1.4965915447213833E+00 -1.4064100117533098E+00 -1.3068099156772481E+00 -1.1977037704145426E+00 -1.0790287129694325E+00 -9.5074811933331249E-01 -8.1285326567377447E-01 -6.6536503136519531E-01 -5.0833563947447913E-01 -3.4185042930888188E-01 -1.6602965458104699E-01 1.8969700330892618E-02 2.1295209463839665E-01 4.1568160561584694E-01 6.2688011410182654E-01 8.4622551298706095E-01 1.0733499518908700E+00 1.3078381326407966E+00 1.5492256718473736E+00 1.7969975489114365E+00 2.0505866603128315E+00 2.3093725040756827E+00 2.5726800219058981E+00 2.8397786306001729E+00 3.1098814787987852E+00 3.3821449697843935E+00 3.6556685955404356E+00 3.9294951313716555E+00 4.2026112437648715E+00 4.4739485665957339E+00 4.7423853021218489E+00 5.0067484034032939E+00 5.2658163939151139E+00 5.5183228782900944E+00 5.7629607955111108E+00 5.9983874626040699E+00 6.2232304530584868E+00 6.4360943498403618E+00 6.6355684078969412E+00 6.8202351553434388E+00 6.9886799558663268E+00 7.1395015470363337E+00 7.2713235599406554E+00 7.3828070145639852E+00 7.4726637724387217E+00 7.5396709130400019E+00 7.5826859830580338E+00 7.6006630479199693E+00 7.5926694526951888E+00 7.5579031748037435E+00 7.4957106238352278E+00 7.4056047144402983E+00 7.2872830069413999E+00 7.1406456773997489E+00 6.9658130448634514E+00 6.7631423490257889E+00 6.5332434372819357E+00 6.2769929870401979E+00 5.9955468580715943E+00 5.6903501416985147E+00 5.3631444498124967E+00 5.0159719681899739E+00 4.6511757864837575E+00 4.2713960127700794E+00 3.8795611848358766E+00 3.4788745047902823E+00 3.0727944495061967E+00 2.6650093484640416E+00 2.2594055746436976E+00 1.8600290653962466E+00 1.4710399802791263E+00 1.0966604180619481E+00 7.4111524837663023E-01 4.0856628206928508E-01 1.0304019615955809E-01 -1.7164914611485163E-01 -4.1198308485661733E-01 -6.1482408323254401E-01 -7.7750368767302169E-01 -8.9791070801467765E-01 -9.7457745379726080E-01 -1.0067615184610970E+00 -9.9452027197417547E-01 -9.3877492228435044E-01 -8.4136075811186017E-01 -7.0506001420803788E-01 -5.3361373207690432E-01 -3.3170905273360529E-01 -1.0493860227349944E-01 1.4027095634096720E-01 3.9676350603074512E-01 6.5679263512327513E-01 9.1219571300086921E-01 1.1546018727559046E+00 1.3756713095952169E+00 1.5673615155876608E+00 1.7222141229291976E+00 1.8336539849531788E+00 1.8962900737096624E+00 1.9062058239593591E+00 1.8612248359434862E+00 1.7611365124767293E+00 1.6078654141337378E+00 1.4055680429407162E+00 1.1606415835998511E+00 8.8163100377651571E-01 5.7902397667196881E-01 2.6492743068721902E-01 -4.7374822006681305E-02 -3.4397703554471859E-01 -6.1100475381908881E-01 -8.3534326832428829E-01 -1.0054092134192465E+00 -1.1119244188134341E+00 -1.1486433772158950E+00 -1.1129798174370440E+00 -1.0064748576134166E+00 -8.3505002770354453E-01 -6.0899400362767120E-01 -3.4264291265785790E-01 -5.3730958560219484E-02 2.3758918057483747E-01 5.1002887353644977E-01 7.4269005933865906E-01 9.1674370483262457E-01 1.0171364675951045E+00 1.0341754237196570E+00 9.6482382327285909E-01 8.1353785219605290E-01 5.9248931505937730E-01 3.2105496095539710E-01 2.4510999759080790E-02 -2.6805022927552358E-01 -5.2647012618742739E-01 -7.2272692728374655E-01 -8.3428095253506207E-01 -8.4717223238536243E-01 -7.5843757656368449E-01 -5.7742241749082046E-01 -3.2563498142413089E-01 -3.4932318414599664E-02 2.5596475596454610E-01 5.0637457588186396E-01 6.7944807282589625E-01 7.4807686423199715E-01 6.9996898981991751E-01 5.4090449950355124E-01 2.9531564000429888E-01 3.6629582774235139E-03 -2.8341470651363038E-01 -5.1356901875941185E-01 -6.4257288083515873E-01 -6.4372538437646498E-01 -5.1478468066985217E-01 -2.8053103228888099E-01 1.0307477480476321E-02 2.9394888562629151E-01 5.0506874923440293E-01 5.9232880680216971E-01 5.3228940512931178E-01 3.3779355998875571E-01 5.7672569594563863E-02 -2.3351872373185353E-01 -4.5434831648047996E-01 -5.3966957157889750E-01 -4.6164791418236700E-01 -2.4162733363890637E-01 5.2508498916432833E-02 3.2488294495339121E-01 4.8211383512758371E-01 4.6662813324524616E-01 2.8084029049768455E-01 -8.5506847570315757E-03 -2.9100424233102423E-01 -4.5287741575608875E-01 -4.2447023825396396E-01 -2.1386840125430395E-01 8.9743629224072488E-02 3.4970591424002101E-01 4.4224700446785725E-01 3.1806133041313983E-01 3.3935346793816143E-02 -2.6700190788952560E-01 -4.2399234283998705E-01 -3.4588739846095778E-01 -6.9724933912096290E-02 2.4874894773970616E-01 4.1793706265675001E-01 3.2652034090510551E-01 2.3084873606199093E-02 -2.9990748288080948E-01 -4.2267552039278766E-01 -2.4961404722139593E-01 1.0850927996791032E-01 3.9472170096381270E-01 3.8621294021839336E-01 7.2986834403458947E-02 -3.1021956073382373E-01 -4.5033019326900237E-01 -2.1264459644616199E-01 2.2114217883912712E-01 4.7766193390457362E-01 3.0997709996627193E-01 -1.5652609715587804E-01 -4.9898429677660888E-01 -3.7382281637591458E-01 1.3111421863061049E-01 5.3348835715042875E-01 4.0879596319304273E-01 -1.5427533415207106E-01 -5.8784669674852219E-01 -4.0913071254923400E-01 2.3322763338095864E-01 6.5458815037440576E-01 3.5787371661350748E-01 -3.6923710099021634E-01 -7.0911907290263165E-01 -2.3222147076131319E-01 5.4796390959572094E-01 7.0963437027126164E-01 1.6987243314278394E-02 -7.2900871968949255E-01 -6.0681391971886689E-01 2.7549709061199334E-01 8.4456186796075428E-01 3.6727617881735131E-01 -5.8895682235424296E-01 -8.1756642214151631E-01 -4.2137793741517287E-03 8.2656979934510832E-01 5.9934862269970901E-01 -4.0169574191175883E-01 -8.9418645250379358E-01 -1.8054147946644658E-01 6.4368605193197015E-01 8.5294310342479884E-01 -8.2846530713927020E-04 -4.8159152332642883E+00 2.5174106137014665E+01 -1.2568828668601327E+02 5.2745336276027388E+02 -1.8186619345853182E+03 4.3436504440982226E+03 2.3658244185862759E+03 -1.2225293629273554E+05 1.0652457834610241E+06 -6.8929993568228409E+06 3.7755721260872029E+07 -1.7718629020249790E+08 6.5936028742821777E+08 </ae_partial_wave> <pseudo_partial_wave state= "Ni2" grid="log1"> -1.9466261703328563E-01 -1.9466261738257043E-01 -1.9466261845452887E-01 -1.9466262028598852E-01 -1.9466262291531458E-01 -1.9466262638240989E-01 -1.9466263072875639E-01 -1.9466263599747161E-01 -1.9466264223337590E-01 -1.9466264948305509E-01 -1.9466265779491648E-01 -1.9466266721926775E-01 -1.9466267780837732E-01 -1.9466268961653543E-01 -1.9466270270015681E-01 -1.9466271711783281E-01 -1.9466273293042041E-01 -1.9466275020111445E-01 -1.9466276899555088E-01 -1.9466278938187773E-01 -1.9466281143084843E-01 -1.9466283521592970E-01 -1.9466286081337719E-01 -1.9466288830235681E-01 -1.9466291776503680E-01 -1.9466294928669875E-01 -1.9466298295585727E-01 -1.9466301886435397E-01 -1.9466305710750686E-01 -1.9466309778420923E-01 -1.9466314099707513E-01 -1.9466318685256329E-01 -1.9466323546111913E-01 -1.9466328693730994E-01 -1.9466334139997987E-01 -1.9466339897240298E-01 -1.9466345978243457E-01 -1.9466352396267561E-01 -1.9466359165065328E-01 -1.9466366298897608E-01 -1.9466373812553697E-01 -1.9466381721368142E-01 -1.9466390041241471E-01 -1.9466398788658959E-01 -1.9466407980713049E-01 -1.9466417635124947E-01 -1.9466427770262920E-01 -1.9466438405171910E-01 -1.9466449559590795E-01 -1.9466461253982204E-01 -1.9466473509554763E-01 -1.9466486348291473E-01 -1.9466499792975547E-01 -1.9466513867218527E-01 -1.9466528595492447E-01 -1.9466544003156450E-01 -1.9466560116490220E-01 -1.9466576962726223E-01 -1.9466594570081650E-01 -1.9466612967796185E-01 -1.9466632186164293E-01 -1.9466652256575848E-01 -1.9466673211552135E-01 -1.9466695084786778E-01 -1.9466717911186260E-01 -1.9466741726913908E-01 -1.9466766569431931E-01 -1.9466792477547828E-01 -1.9466819491463402E-01 -1.9466847652821584E-01 -1.9466877004756139E-01 -1.9466907591946617E-01 -1.9466939460670613E-01 -1.9466972658860410E-01 -1.9467007236160727E-01 -1.9467043243987858E-01 -1.9467080735593706E-01 -1.9467119766127733E-01 -1.9467160392705093E-01 -1.9467202674472978E-01 -1.9467246672684987E-01 -1.9467292450771168E-01 -1.9467340074416775E-01 -1.9467389611639735E-01 -1.9467441132871460E-01 -1.9467494711042263E-01 -1.9467550421667684E-01 -1.9467608342940321E-01 -1.9467668555819154E-01 -1.9467731144130843E-01 -1.9467796194666606E-01 -1.9467863797286114E-01 -1.9467934045024166E-01 -1.9468007034202070E-01 -1.9468082864540892E-01 -1.9468161639280673E-01 -1.9468243465302446E-01 -1.9468328453254452E-01 -1.9468416717683540E-01 -1.9468508377171725E-01 -1.9468603554474589E-01 -1.9468702376666935E-01 -1.9468804975292919E-01 -1.9468911486522117E-01 -1.9469022051309090E-01 -1.9469136815559565E-01 -1.9469255930302598E-01 -1.9469379551868943E-01 -1.9469507842074010E-01 -1.9469640968407270E-01 -1.9469779104232754E-01 -1.9469922428988340E-01 -1.9470071128399610E-01 -1.9470225394695057E-01 -1.9470385426834891E-01 -1.9470551430740335E-01 -1.9470723619538560E-01 -1.9470902213809843E-01 -1.9471087441846274E-01 -1.9471279539919117E-01 -1.9471478752555543E-01 -1.9471685332822150E-01 -1.9471899542625692E-01 -1.9472121653011820E-01 -1.9472351944486838E-01 -1.9472590707344131E-01 -1.9472838242000193E-01 -1.9473094859347323E-01 -1.9473360881114415E-01 -1.9473636640243869E-01 -1.9473922481275316E-01 -1.9474218760750467E-01 -1.9474525847626412E-01 -1.9474844123703938E-01 -1.9475173984072039E-01 -1.9475515837567128E-01 -1.9475870107248117E-01 -1.9476237230887150E-01 -1.9476617661477597E-01 -1.9477011867760649E-01 -1.9477420334767387E-01 -1.9477843564383726E-01 -1.9478282075928868E-01 -1.9478736406760380E-01 -1.9479207112894531E-01 -1.9479694769650058E-01 -1.9480199972316739E-01 -1.9480723336839445E-01 -1.9481265500536760E-01 -1.9481827122832882E-01 -1.9482408886022967E-01 -1.9483011496060776E-01 -1.9483635683374897E-01 -1.9484282203711292E-01 -1.9484951839007325E-01 -1.9485645398294271E-01 -1.9486363718629876E-01 -1.9487107666066220E-01 -1.9487878136646214E-01 -1.9488676057439153E-01 -1.9489502387607777E-01 -1.9490358119514184E-01 -1.9491244279865130E-01 -1.9492161930890786E-01 -1.9493112171571686E-01 -1.9494096138901224E-01 -1.9495115009196223E-01 -1.9496169999449495E-01 -1.9497262368729404E-01 -1.9498393419629642E-01 -1.9499564499763758E-01 -1.9500777003317799E-01 -1.9502032372649891E-01 -1.9503332099947790E-01 -1.9504677728943295E-01 -1.9506070856683611E-01 -1.9507513135366431E-01 -1.9509006274234986E-01 -1.9510552041539095E-01 -1.9512152266562677E-01 -1.9513808841724450E-01 -1.9515523724743189E-01 -1.9517298940885186E-01 -1.9519136585283331E-01 -1.9521038825336190E-01 -1.9523007903192846E-01 -1.9525046138318256E-01 -1.9527155930146592E-01 -1.9529339760831699E-01 -1.9531600198080482E-01 -1.9533939898095359E-01 -1.9536361608607505E-01 -1.9538868172019058E-01 -1.9541462528650580E-01 -1.9544147720101754E-01 -1.9546926892721911E-01 -1.9549803301205271E-01 -1.9552780312304874E-01 -1.9555861408673897E-01 -1.9559050192838603E-01 -1.9562350391305106E-01 -1.9565765858810663E-01 -1.9569300582713367E-01 -1.9572958687536304E-01 -1.9576744439665750E-01 -1.9580662252205380E-01 -1.9584716690001897E-01 -1.9588912474836381E-01 -1.9593254490796044E-01 -1.9597747789825581E-01 -1.9602397597468638E-01 -1.9607209318804233E-01 -1.9612188544586123E-01 -1.9617341057585433E-01 -1.9622672839155203E-01 -1.9628190076015159E-01 -1.9633899167261978E-01 -1.9639806731623913E-01 -1.9645919614957355E-01 -1.9652244897996901E-01 -1.9658789904368548E-01 -1.9665562208874870E-01 -1.9672569646056487E-01 -1.9679820319046873E-01 -1.9687322608723495E-01 -1.9695085183167113E-01 -1.9703117007442769E-01 -1.9711427353705632E-01 -1.9720025811651887E-01 -1.9728922299316665E-01 -1.9738127074239253E-01 -1.9747650744996920E-01 -1.9757504283133448E-01 -1.9767699035480973E-01 -1.9778246736897132E-01 -1.9789159523429567E-01 -1.9800449945916981E-01 -1.9812130984048815E-01 -1.9824216060889541E-01 -1.9836719057889815E-01 -1.9849654330396008E-01 -1.9863036723677174E-01 -1.9876881589481088E-01 -1.9891204803142179E-01 -1.9906022781256116E-01 -1.9921352499935691E-01 -1.9937211513676251E-01 -1.9953617974836146E-01 -1.9970590653763962E-01 -1.9988148959586446E-01 -2.0006312961679573E-01 -2.0025103411840148E-01 -2.0044541767188892E-01 -2.0064650213817553E-01 -2.0085451691207445E-01 -2.0106969917445525E-01 -2.0129229415256547E-01 -2.0152255538879765E-01 -2.0176074501818606E-01 -2.0200713405477222E-01 -2.0226200268730685E-01 -2.0252564058435696E-01 -2.0279834720922743E-01 -2.0308043214495072E-01 -2.0337221542961167E-01 -2.0367402790234548E-01 -2.0398621156029709E-01 -2.0430911992684794E-01 -2.0464311843144331E-01 -2.0498858480131421E-01 -2.0534590946549935E-01 -2.0571549597141828E-01 -2.0609776141434225E-01 -2.0649313688021845E-01 -2.0690206790206972E-01 -2.0732501493038846E-01 -2.0776245381790376E-01 -2.0821487631906657E-01 -2.0868279060458553E-01 -2.0916672179150597E-01 -2.0966721248905013E-01 -2.1018482336075495E-01 -2.1072013370318513E-01 -2.1127374204161822E-01 -2.1184626674316803E-01 -2.1243834664759270E-01 -2.1305064171630347E-01 -2.1368383369987137E-01 -2.1433862682442417E-01 -2.1501574849730729E-01 -2.1571595003239855E-01 -2.1644000739539471E-01 -2.1718872196940095E-01 -2.1796292134126169E-01 -2.1876346010879016E-01 -2.1959122070936507E-01 -2.2044711427007285E-01 -2.2133208147972508E-01 -2.2224709348292149E-01 -2.2319315279650054E-01 -2.2417129424843504E-01 -2.2518258593939181E-01 -2.2622813022710900E-01 -2.2730906473357421E-01 -2.2842656337512185E-01 -2.2958183741543131E-01 -2.3077613654124909E-01 -2.3201074996086063E-01 -2.3328700752497486E-01 -2.3460628086984392E-01 -2.3596998458220861E-01 -2.3737957738565485E-01 -2.3883656334785558E-01 -2.4034249310803033E-01 -2.4189896512390682E-01 -2.4350762693727343E-01 -2.4517017645715999E-01 -2.4688836325944205E-01 -2.4866398990160465E-01 -2.5049891325117424E-01 -2.5239504582612360E-01 -2.5435435714542287E-01 -2.5637887508767448E-01 -2.5847068725546390E-01 -2.6063194234290232E-01 -2.6286485150356359E-01 -2.6517168971561111E-01 -2.6755479714074831E-01 -2.7001658047323318E-01 -2.7255951427474023E-01 -2.7518614229065369E-01 -2.7789907874273406E-01 -2.8070100959293198E-01 -2.8359469377226193E-01 -2.8658296436859465E-01 -2.8966872976617414E-01 -2.9285497472956890E-01 -2.9614476142370572E-01 -2.9954123036124325E-01 -3.0304760126766284E-01 -3.0666717385378151E-01 -3.1040332848443680E-01 -3.1425952673138569E-01 -3.1823931179729004E-01 -3.2234630879689086E-01 -3.2658422488021366E-01 -3.3095684918161861E-01 -3.3546805257722340E-01 -3.4012178723195097E-01 -3.4492208591613199E-01 -3.4987306106998267E-01 -3.5497890359296008E-01 -3.6024388133301638E-01 -3.6567233724936077E-01 -3.7126868722023948E-01 -3.7703741746536501E-01 -3.8298308155057476E-01 -3.8911029693994797E-01 -3.9542374105848788E-01 -4.0192814682583589E-01 -4.0862829761891895E-01 -4.1552902161875949E-01 -4.2263518549371004E-01 -4.2995168736835099E-01 -4.3748344902405295E-01 -4.4523540727392530E-01 -4.5321250445127298E-01 -4.6141967794691496E-01 -4.6986184872703313E-01 -4.7854390875895048E-01 -4.8747070726814229E-01 -4.9664703574531893E-01 -5.0607761161780962E-01 -5.1576706049475829E-01 -5.2571989689060450E-01 -5.3594050332626375E-01 -5.4643310770210562E-01 -5.5720175883137368E-01 -5.6825030001703558E-01 -5.7958234054938762E-01 -5.9120122499586036E-01 -6.0311000014837246E-01 -6.1531137948773007E-01 -6.2780770501830152E-01 -6.4060090632014188E-01 -6.5369245665961961E-01 -6.6708332599353548E-01 -6.8077393069578473E-01 -6.9476407982979149E-01 -7.0905291778451685E-01 -7.2363886308638281E-01 -7.3851954319483415E-01 -7.5369172508464466E-01 -7.6915124141447377E-01 -7.8489291207800327E-01 -8.0091046093160168E-01 -8.1719642749155941E-01 -8.3374207339336726E-01 -8.5053728340709822E-01 -8.6757046080546374E-01 -8.8482841688577185E-01 -9.0229625445344408E-01 -9.1995724508354115E-01 -9.3779269998814918E-01 -9.5578183433161690E-01 -9.7390162485323106E-01 -9.9212666067791122E-01 -1.0104289872207659E+00 -1.0287779431208202E+00 -1.0471399901740250E+00 -1.0654785362755901E+00 -1.0837537514278628E+00 -1.1019223769229245E+00 -1.1199375278688757E+00 -1.1377484892971419E+00 -1.1553005061645483E+00 -1.1725345676503445E+00 -1.1893871862444851E+00 -1.2057901722310083E+00 -1.2216704042895339E+00 -1.2369495970700117E+00 -1.2515440667413922E+00 -1.2653644956751791E+00 -1.2783156976003485E+00 -1.2902963847581310E+00 -1.3011989387941181E+00 -1.3109091873522265E+00 -1.3193061885808663E+00 -1.3262620260264337E+00 -1.3316416166746192E+00 -1.3353025352046173E+00 -1.3370948578472841E+00 -1.3368610295839767E+00 -1.3344357587887070E+00 -1.3296459438014161E+00 -1.3223106363237376E+00 -1.3122410469486185E+00 -1.2992405985700370E+00 -1.2831050338657561E+00 -1.2636225835010451E+00 -1.2405742021609580E+00 -1.2137338799769564E+00 -1.1828690373653024E+00 -1.1477410117312099E+00 -1.1081056449068836E+00 -1.0637139805719151E+00 -1.0143130812406844E+00 -9.5964697467918381E-01 -8.9945773981869404E-01 -8.3348674234867048E-01 -7.6147603017704657E-01 -6.8316989882175694E-01 -5.9831663651953182E-01 -5.0667045838099889E-01 -4.0799363825710316E-01 -3.0205884608113437E-01 -1.8865169728065939E-01 -6.7573519381001229E-02 6.1355660889036490E-02 1.9829390886442785E-01 3.4337395305736468E-01 4.9669954063686317E-01 6.5834158532660048E-01 8.2833411982449157E-01 1.0066700694478181E+00 1.1932968688846393E+00 1.3881119497022569E+00 1.5909581326388418E+00 1.8016189656822990E+00 2.0198140565069953E+00 2.2451944559606507E+00 2.4773381579188394E+00 2.7157457898758603E+00 2.9598365780131504E+00 3.2089446800441013E+00 3.4623159887025521E+00 3.7191055181091897E+00 3.9783754941567060E+00 4.2390942781959300E+00 4.5001362603232984E+00 4.7602828640563386E+00 5.0182248076744722E+00 5.2725657684808160E+00 5.5218275941424979E+00 5.7644571994807485E+00 5.9988352769675215E+00 6.2232869340737054E+00 6.4360943498403618E+00 6.6355684078969412E+00 6.8202351553434388E+00 6.9886799558663268E+00 7.1395015470363337E+00 7.2713235599406554E+00 7.3828070145639852E+00 7.4726637724387217E+00 7.5396709130400019E+00 7.5826859830580338E+00 7.6006630479199693E+00 7.5926694526951888E+00 7.5579031748037435E+00 7.4957106238352278E+00 7.4056047144402983E+00 7.2872830069413999E+00 7.1406456773997489E+00 6.9658130448634514E+00 6.7631423490257889E+00 6.5332434372819357E+00 6.2769929870401979E+00 5.9955468580715943E+00 5.6903501416985147E+00 5.3631444498124967E+00 5.0159719681899739E+00 4.6511757864837575E+00 4.2713960127700794E+00 3.8795611848358766E+00 3.4788745047902823E+00 3.0727944495061967E+00 2.6650093484640416E+00 2.2594055746436976E+00 1.8600290653962466E+00 1.4710399802791263E+00 1.0966604180619481E+00 7.4111524837663023E-01 4.0856628206928508E-01 1.0304019615955809E-01 -1.7164914611485163E-01 -4.1198308485661733E-01 -6.1482408323254401E-01 -7.7750368767302169E-01 -8.9791070801467765E-01 -9.7457745379726080E-01 -1.0067615184610970E+00 -9.9452027197417547E-01 -9.3877492228435044E-01 -8.4136075811186017E-01 -7.0506001420803788E-01 -5.3361373207690432E-01 -3.3170905273360529E-01 -1.0493860227349944E-01 1.4027095634096720E-01 3.9676350603074512E-01 6.5679263512327513E-01 9.1219571300086921E-01 1.1546018727559046E+00 1.3756713095952169E+00 1.5673615155876608E+00 1.7222141229291976E+00 1.8336539849531788E+00 1.8962900737096624E+00 1.9062058239593591E+00 1.8612248359434862E+00 1.7611365124767293E+00 1.6078654141337378E+00 1.4055680429407162E+00 1.1606415835998511E+00 8.8163100377651571E-01 5.7902397667196881E-01 2.6492743068721902E-01 -4.7374822006681305E-02 -3.4397703554471859E-01 -6.1100475381908881E-01 -8.3534326832428829E-01 -1.0054092134192465E+00 -1.1119244188134341E+00 -1.1486433772158950E+00 -1.1129798174370440E+00 -1.0064748576134166E+00 -8.3505002770354453E-01 -6.0899400362767120E-01 -3.4264291265785790E-01 -5.3730958560219484E-02 2.3758918057483747E-01 5.1002887353644977E-01 7.4269005933865906E-01 9.1674370483262457E-01 1.0171364675951045E+00 1.0341754237196570E+00 9.6482382327285909E-01 8.1353785219605290E-01 5.9248931505937730E-01 3.2105496095539710E-01 2.4510999759080790E-02 -2.6805022927552358E-01 -5.2647012618742739E-01 -7.2272692728374655E-01 -8.3428095253506207E-01 -8.4717223238536243E-01 -7.5843757656368449E-01 -5.7742241749082046E-01 -3.2563498142413089E-01 -3.4932318414599664E-02 2.5596475596454610E-01 5.0637457588186396E-01 6.7944807282589625E-01 7.4807686423199715E-01 6.9996898981991751E-01 5.4090449950355124E-01 2.9531564000429888E-01 3.6629582774235139E-03 -2.8341470651363038E-01 -5.1356901875941185E-01 -6.4257288083515873E-01 -6.4372538437646498E-01 -5.1478468066985217E-01 -2.8053103228888099E-01 1.0307477480476321E-02 2.9394888562629151E-01 5.0506874923440293E-01 5.9232880680216971E-01 5.3228940512931178E-01 3.3779355998875571E-01 5.7672569594563863E-02 -2.3351872373185353E-01 -4.5434831648047996E-01 -5.3966957157889750E-01 -4.6164791418236700E-01 -2.4162733363890637E-01 5.2508498916432833E-02 3.2488294495339121E-01 4.8211383512758371E-01 4.6662813324524616E-01 2.8084029049768455E-01 -8.5506847570315757E-03 -2.9100424233102423E-01 -4.5287741575608875E-01 -4.2447023825396396E-01 -2.1386840125430395E-01 8.9743629224072488E-02 3.4970591424002101E-01 4.4224700446785725E-01 3.1806133041313983E-01 3.3935346793816143E-02 -2.6700190788952560E-01 -4.2399234283998705E-01 -3.4588739846095778E-01 -6.9724933912096290E-02 2.4874894773970616E-01 4.1793706265675001E-01 3.2652034090510551E-01 2.3084873606199093E-02 -2.9990748288080948E-01 -4.2267552039278766E-01 -2.4961404722139593E-01 1.0850927996791032E-01 3.9472170096381270E-01 3.8621294021839336E-01 7.2986834403458947E-02 -3.1021956073382373E-01 -4.5033019326900237E-01 -2.1264459644616199E-01 2.2114217883912712E-01 4.7766193390457362E-01 3.0997709996627193E-01 -1.5652609715587804E-01 -4.9898429677660888E-01 -3.7382281637591458E-01 1.3111421863061049E-01 5.3348835715042875E-01 4.0879596319304273E-01 -1.5427533415207106E-01 -5.8784669674852219E-01 -4.0913071254923400E-01 2.3322763338095864E-01 6.5458815037440576E-01 3.5787371661350748E-01 -3.6923710099021634E-01 -7.0911907290263165E-01 -2.3222147076131319E-01 5.4796390959572094E-01 7.0963437027126164E-01 1.6987243314278394E-02 -7.2900871968949255E-01 -6.0681391971886689E-01 2.7549709061199334E-01 8.4456186796075428E-01 3.6727617881735131E-01 -5.8895682235424296E-01 -8.1756642214151631E-01 -4.2137793741517287E-03 8.2656979934510832E-01 5.9934862269970901E-01 -4.0169574191175883E-01 -8.9418645250379358E-01 -1.8054147946644658E-01 6.4368605193197015E-01 8.5294310342479884E-01 -8.2846530713927020E-04 -4.8159152332642883E+00 2.5174106137014665E+01 -1.2568828668601327E+02 5.2745336276027388E+02 -1.8186619345853182E+03 4.3436504440982226E+03 2.3658244185862759E+03 -1.2225293629273554E+05 1.0652457834610241E+06 -6.8929993568228409E+06 3.7755721260872029E+07 -1.7718629020249790E+08 6.5936028742821777E+08 </pseudo_partial_wave> <projector_function state= "Ni2" grid="log1"> -1.0200234021198489E+00 -1.0200234020360583E+00 -1.0200234017789396E+00 -1.0200234013396481E+00 -1.0200234007089783E+00 -1.0200233998773636E+00 -1.0200233988348535E+00 -1.0200233975711039E+00 -1.0200233960753649E+00 -1.0200233943364636E+00 -1.0200233923427868E+00 -1.0200233900822699E+00 -1.0200233875423772E+00 -1.0200233847100804E+00 -1.0200233815718531E+00 -1.0200233781136410E+00 -1.0200233743208484E+00 -1.0200233701783123E+00 -1.0200233656702953E+00 -1.0200233607804483E+00 -1.0200233554917999E+00 -1.0200233497867308E+00 -1.0200233436469477E+00 -1.0200233370534644E+00 -1.0200233299865702E+00 -1.0200233224258073E+00 -1.0200233143499540E+00 -1.0200233057369708E+00 -1.0200232965639999E+00 -1.0200232868073169E+00 -1.0200232764423127E+00 -1.0200232654434511E+00 -1.0200232537842422E+00 -1.0200232414372050E+00 -1.0200232283738302E+00 -1.0200232145645549E+00 -1.0200231999787097E+00 -1.0200231845844849E+00 -1.0200231683488976E+00 -1.0200231512377409E+00 -1.0200231332155429E+00 -1.0200231142455194E+00 -1.0200230942895336E+00 -1.0200230733080395E+00 -1.0200230512600441E+00 -1.0200230281030431E+00 -1.0200230037929705E+00 -1.0200229782841546E+00 -1.0200229515292396E+00 -1.0200229234791514E+00 -1.0200228940830149E+00 -1.0200228632881063E+00 -1.0200228310397756E+00 -1.0200227972813833E+00 -1.0200227619542372E+00 -1.0200227249975078E+00 -1.0200226863481596E+00 -1.0200226459408774E+00 -1.0200226037079729E+00 -1.0200225595793175E+00 -1.0200225134822398E+00 -1.0200224653414545E+00 -1.0200224150789519E+00 -1.0200223626139164E+00 -1.0200223078626174E+00 -1.0200222507383183E+00 -1.0200221911511593E+00 -1.0200221290080529E+00 -1.0200220642125730E+00 -1.0200219966648401E+00 -1.0200219262613834E+00 -1.0200218528950398E+00 -1.0200217764548036E+00 -1.0200216968257052E+00 -1.0200216138886671E+00 -1.0200215275203570E+00 -1.0200214375930474E+00 -1.0200213439744525E+00 -1.0200212465275793E+00 -1.0200211451105476E+00 -1.0200210395764409E+00 -1.0200209297731080E+00 -1.0200208155429957E+00 -1.0200206967229577E+00 -1.0200205731440504E+00 -1.0200204446313408E+00 -1.0200203110036932E+00 -1.0200201720735564E+00 -1.0200200276467311E+00 -1.0200198775221514E+00 -1.0200197214916364E+00 -1.0200195593396433E+00 -1.0200193908430117E+00 -1.0200192157707020E+00 -1.0200190338835162E+00 -1.0200188449338148E+00 -1.0200186486652312E+00 -1.0200184448123517E+00 -1.0200182331004162E+00 -1.0200180132449874E+00 -1.0200177849516152E+00 -1.0200175479154856E+00 -1.0200173018210632E+00 -1.0200170463417246E+00 -1.0200167811393592E+00 -1.0200165058639841E+00 -1.0200162201533280E+00 -1.0200159236323976E+00 -1.0200156159130493E+00 -1.0200152965935139E+00 -1.0200149652579484E+00 -1.0200146214759274E+00 -1.0200142648019475E+00 -1.0200138947748991E+00 -1.0200135109175348E+00 -1.0200131127358960E+00 -1.0200126997187469E+00 -1.0200122713369695E+00 -1.0200118270429435E+00 -1.0200113662699080E+00 -1.0200108884312984E+00 -1.0200103929200548E+00 -1.0200098791079304E+00 -1.0200093463447300E+00 -1.0200087939575773E+00 -1.0200082212501136E+00 -1.0200076275016896E+00 -1.0200070119665281E+00 -1.0200063738728493E+00 -1.0200057124219790E+00 -1.0200050267874092E+00 -1.0200043161138437E+00 -1.0200035795161990E+00 -1.0200028160785768E+00 -1.0200020248531949E+00 -1.0200012048592888E+00 -1.0200003550819692E+00 -1.0199994744710519E+00 -1.0199985619398211E+00 -1.0199976163637869E+00 -1.0199966365793647E+00 -1.0199956213825385E+00 -1.0199945695274486E+00 -1.0199934797249661E+00 -1.0199923506411841E+00 -1.0199911808958793E+00 -1.0199899690609096E+00 -1.0199887136585588E+00 -1.0199874131598363E+00 -1.0199860659826929E+00 -1.0199846704902009E+00 -1.0199832249886571E+00 -1.0199817277256260E+00 -1.0199801768879089E+00 -1.0199785705994553E+00 -1.0199769069191897E+00 -1.0199751838387716E+00 -1.0199733992802762E+00 -1.0199715510937928E+00 -1.0199696370549531E+00 -1.0199676548623458E+00 -1.0199656021348777E+00 -1.0199634764090268E+00 -1.0199612751359886E+00 -1.0199589956787487E+00 -1.0199566353090392E+00 -1.0199541912041952E+00 -1.0199516604439058E+00 -1.0199490400068407E+00 -1.0199463267671860E+00 -1.0199435174910279E+00 -1.0199406088326479E+00 -1.0199375973306548E+00 -1.0199344794040128E+00 -1.0199312513479217E+00 -1.0199279093295492E+00 -1.0199244493836261E+00 -1.0199208674078926E+00 -1.0199171591583764E+00 -1.0199133202445114E+00 -1.0199093461241082E+00 -1.0199052320981143E+00 -1.0199009733052369E+00 -1.0198965647163489E+00 -1.0198920011287105E+00 -1.0198872771600094E+00 -1.0198823872421758E+00 -1.0198773256149851E+00 -1.0198720863194672E+00 -1.0198666631910507E+00 -1.0198610498525058E+00 -1.0198552397066256E+00 -1.0198492259286633E+00 -1.0198430014585067E+00 -1.0198365589925906E+00 -1.0198298909755221E+00 -1.0198229895914219E+00 -1.0198158467549849E+00 -1.0198084541022008E+00 -1.0198008029807906E+00 -1.0197928844402853E+00 -1.0197846892217990E+00 -1.0197762077474137E+00 -1.0197674301092277E+00 -1.0197583460580191E+00 -1.0197489449915147E+00 -1.0197392159422722E+00 -1.0197291475651284E+00 -1.0197187281242366E+00 -1.0197079454796467E+00 -1.0196967870734290E+00 -1.0196852399153209E+00 -1.0196732905678934E+00 -1.0196609251311934E+00 -1.0196481292268669E+00 -1.0196348879817474E+00 -1.0196211860108704E+00 -1.0196070073999095E+00 -1.0195923356870196E+00 -1.0195771538440481E+00 -1.0195614442571108E+00 -1.0195451887065012E+00 -1.0195283683459118E+00 -1.0195109636809516E+00 -1.0194929545469156E+00 -1.0194743200858098E+00 -1.0194550387225876E+00 -1.0194350881405638E+00 -1.0194144452560039E+00 -1.0193930861918372E+00 -1.0193709862504741E+00 -1.0193481198856991E+00 -1.0193244606735972E+00 -1.0192999812825021E+00 -1.0192746534419013E+00 -1.0192484479103001E+00 -1.0192213344419745E+00 -1.0191932817526046E+00 -1.0191642574837290E+00 -1.0191342281659874E+00 -1.0191031591811144E+00 -1.0190710147226538E+00 -1.0190377577553087E+00 -1.0190033499729296E+00 -1.0189677517550721E+00 -1.0189309221220648E+00 -1.0188928186885788E+00 -1.0188533976155778E+00 -1.0188126135606823E+00 -1.0187704196268188E+00 -1.0187267673091454E+00 -1.0186816064401538E+00 -1.0186348851329432E+00 -1.0185865497225504E+00 -1.0185365447052961E+00 -1.0184848126760870E+00 -1.0184312942635894E+00 -1.0183759280632081E+00 -1.0183186505678261E+00 -1.0182593960961548E+00 -1.0181980967187221E+00 -1.0181346821813262E+00 -1.0180690798259273E+00 -1.0180012145088591E+00 -1.0179310085163018E+00 -1.0178583814769031E+00 -1.0177832502714588E+00 -1.0177055289395651E+00 -1.0176251285831375E+00 -1.0175419572666686E+00 -1.0174559199141846E+00 -1.0173669182027207E+00 -1.0172748504522209E+00 -1.0171796115117886E+00 -1.0170810926421119E+00 -1.0169791813939664E+00 -1.0168737614826695E+00 -1.0167647126583599E+00 -1.0166519105719261E+00 -1.0165352266365175E+00 -1.0164145278844214E+00 -1.0162896768192016E+00 -1.0161605312629456E+00 -1.0160269441984211E+00 -1.0158887636060463E+00 -1.0157458322954418E+00 -1.0155979877314543E+00 -1.0154450618544166E+00 -1.0152868808944981E+00 -1.0151232651799658E+00 -1.0149540289391250E+00 -1.0147789800957896E+00 -1.0145979200580244E+00 -1.0144106435000158E+00 -1.0142169381367849E+00 -1.0140165844915747E+00 -1.0138093556556620E+00 -1.0135950170403591E+00 -1.0133733261209534E+00 -1.0131440321723817E+00 -1.0129068759963256E+00 -1.0126615896394935E+00 -1.0124078961028478E+00 -1.0121455090414337E+00 -1.0118741324545946E+00 -1.0115934603662438E+00 -1.0113031764948819E+00 -1.0110029539131054E+00 -1.0106924546962115E+00 -1.0103713295596493E+00 -1.0100392174849349E+00 -1.0096957453336921E+00 -1.0093405274494911E+00 -1.0089731652470841E+00 -1.0085932467887075E+00 -1.0082003463470173E+00 -1.0077940239543031E+00 -1.0073738249375672E+00 -1.0069392794390244E+00 -1.0064899019216318E+00 -1.0060251906591791E+00 -1.0055446272104795E+00 -1.0050476758772320E+00 -1.0045337831450218E+00 -1.0040023771069835E+00 -1.0034528668696265E+00 -1.0028846419402584E+00 -1.0022970715954824E+00 -1.0016895042302021E+00 -1.0010612666865191E+00 -1.0004116635619675E+00 -9.9973997649637703E-01 -9.9904546343681444E-01 -9.9832735787980054E-01 -9.9758486809022906E-01 -9.9681717629612232E-01 -9.9602343785856895E-01 -9.9520278041596244E-01 -9.9435430300175098E-01 -9.9347707513479855E-01 -9.9257013588145804E-01 -9.9163249288837219E-01 -9.9066312138501822E-01 -9.8966096315490482E-01 -9.8862492547431602E-01 -9.8755388001741307E-01 -9.8644666172644180E-01 -9.8530206764574024E-01 -9.8411885571809998E-01 -9.8289574354206521E-01 -9.8163140708850871E-01 -9.8032447937490530E-01 -9.7897354909542977E-01 -9.7757715920503907E-01 -9.7613380545551698E-01 -9.7464193488130590E-01 -9.7309994423286850E-01 -9.7150617835510522E-01 -9.6985892850825506E-01 -9.6815643062849799E-01 -9.6639686352529830E-01 -9.6457834701235690E-01 -9.6269893996882738E-01 -9.6075663832724556E-01 -9.5874937298439056E-01 -9.5667500763108115E-01 -9.5453133649669564E-01 -9.5231608200391848E-01 -9.5002689232902948E-01 -9.4766133886277493E-01 -9.4521691356664694E-01 -9.4269102621917378E-01 -9.4008100154659835E-01 -9.3738407623213016E-01 -9.3459739579783474E-01 -9.3171801135304277E-01 -9.2874287620314600E-01 -9.2566884231258717E-01 -9.2249265661594504E-01 -9.1921095717116996E-01 -9.1582026914933212E-01 -9.1231700065556054E-01 -9.0869743837656425E-01 -9.0495774305080368E-01 -9.0109394475842308E-01 -8.9710193802932348E-01 -8.9297747676937833E-01 -8.8871616900666262E-01 -8.8431347146207917E-01 -8.7976468395151775E-01 -8.7506494363016252E-01 -8.7020921909361404E-01 -8.6519230435526329E-01 -8.6000881272496854E-01 -8.5465317062062585E-01 -8.4911961135167824E-01 -8.4340216892251563E-01 -8.3749467191350713E-01 -8.3139073750901804E-01 -8.2508376575467002E-01 -8.1856693414091131E-01 -8.1183319262662701E-01 -8.0487525923518521E-01 -7.9768561637634505E-01 -7.9025650807074210E-01 -7.8257993827964922E-01 -7.7464767057129225E-01 -7.6645122938650689E-01 -7.5798190320092929E-01 -7.4923074991837157E-01 -7.4018860487052207E-01 -7.3084609184161786E-01 -7.2119363758320221E-01 -7.1122149033316273E-01 -7.0091974290491699E-01 -6.9027836096605943E-01 -6.7928721718084706E-01 -6.6793613194640122E-01 -6.5621492150780103E-01 -6.4411345429083000E-01 -6.3162171634176334E-01 -6.1872988680915020E-01 -6.0542842444123812E-01 -5.9170816610150123E-01 -5.7756043832123638E-01 -5.6297718290838539E-01 -5.4795109761220750E-01 -5.3247579279949819E-01 -5.1654596502480110E-01 -5.0015758826933499E-01 -4.8330812347484536E-01 -4.6599674680349368E-01 -4.4822459680594950E-01 -4.2999504037064362E-01 -4.1131395695013606E-01 -3.9219004010917341E-01 -3.7263511490619627E-01 -3.5266446900005533E-01 -3.3229719466116381E-01 -3.1155653805764078E-01 -2.9047025128050963E-01 -2.6907094156811096E-01 -2.4739641109279270E-01 -2.2548997949011371E-01 -2.0340078005501136E-01 -1.8118401921855340E-01 -1.5890118757808744E-01 -1.3662020941496947E-01 -1.1441551633904463E-01 -9.2368029498671303E-02 -7.0565033751443088E-02 -4.9099926378183494E-02 -2.8071822429017016E-02 -7.5849987172119260E-03 1.2251841058572749E-02 3.1326496446730925E-02 4.9524410055658261E-02 6.6730028528909816E-02 8.2828392052292421E-02 9.7706954289212458E-02 1.1125762760382440E-01 1.2337903962855989E-01 1.3397897647156456E-01 1.4297697497699072E-01 1.5030701133771468E-01 1.5592021599801656E-01 1.5978752529660240E-01 1.6190215902183372E-01 1.6228179061336748E-01 1.6097025419049715E-01 1.5803861150731041E-01 1.5358538462407928E-01 1.4773574971974812E-01 1.4063948828809145E-01 1.3246750941615779E-01 1.2340679772500159E-01 1.1365371399467639E-01 1.0340568885082382E-01 9.2851514388889778E-02 8.2160664748752749E-02 7.1472374257111726E-02 6.0885578733740120E-02 5.0451286357938038E-02 4.0169488430836842E-02 2.9993340076158670E-02 1.9844021224760582E-02 9.6404058199754152E-03 5.9299242076115148E-04 -2.5761282118882348E-04 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 </projector_function> <ae_partial_wave state= "Ni3" grid="log1"> 3.1476841497228049E-04 1.5815429433616009E-03 2.6265448174366828E-03 3.5461061047650563E-03 4.3984983197645332E-03 5.2039324237032041E-03 5.9834349082575136E-03 6.7425540620808487E-03 7.4854818679879866E-03 8.2171681475195820E-03 8.9404106360630713E-03 9.6572952023487712E-03 1.0369839849477815E-02 1.1079529059478444E-02 1.1787619183919270E-02 1.2495200931534004E-02 1.3203206719188121E-02 1.3912455515607764E-02 1.4623674218478291E-02 1.5337514352876887E-02 1.6054565845240638E-02 1.6775367536941907E-02 1.7500415565850129E-02 1.8230170135827898E-02 1.8965061026612599E-02 1.9705492128018583E-02 2.0451845204835149E-02 2.1204483048120448E-02 2.1963752132466843E-02 2.2729984871862396E-02 2.3503501546725068E-02 2.4284611959560519E-02 2.5073616865132035E-02 2.5870809212101730E-02 2.6676475226136236E-02 2.7490895358987126E-02 2.8314345123703375E-02 2.9147095832651342E-02 2.9989415252212999E-02 3.0841568185758322E-02 3.1703816994632657E-02 3.2576422065377454E-02 3.3459642230147239E-02 3.4353735146245637E-02 3.5258957639836407E-02 3.6175566018161666E-02 3.7103816353990286E-02 3.8043964745507204E-02 3.8996267554419942E-02 3.9960981624690112E-02 4.0938364483983379E-02 4.1928674529662945E-02 4.2932171200920716E-02 4.3949115138442366E-02 4.4979768332831162E-02 4.6024394262867238E-02 4.7083258024550330E-02 4.8156626451762073E-02 4.9244768229286216E-02 5.0347953998839179E-02 5.1466456458688969E-02 5.2600550457373781E-02 5.3750513081973296E-02 5.4916623741334783E-02 5.6099164244609499E-02 5.7298418875414953E-02 5.8514674461901804E-02 5.9748220442972053E-02 6.0999348930866157E-02 6.2268354770310647E-02 6.3555535594393670E-02 6.4861191877315941E-02 6.6185626984143736E-02 6.7529147217674557E-02 6.8892061862508930E-02 7.0274683226407855E-02 7.1677326679002049E-02 7.3100310687906317E-02 7.4543956852281448E-02 7.6008589933875464E-02 7.7494537885565623E-02 7.9002131877414297E-02 8.0531706320242702E-02 8.2083598886718345E-02 8.3658150529944547E-02 8.5255705499533638E-02 8.6876611355137287E-02 8.8521218977402408E-02 9.0189882576313829E-02 9.1882959696878597E-02 9.3600811222102481E-02 9.5343801373201226E-02 9.7112297706986428E-02 9.8906671110357516E-02 1.0072729579182869E-01 1.0257454927001337E-01 1.0444881235898300E-01 1.0635046915041398E-01 1.0827990699242941E-01 1.1023751646503924E-01 1.1222369135207622E-01 1.1423882860952153E-01 1.1628332833010825E-01 1.1835759370408591E-01 1.2046203097602587E-01 1.2259704939754110E-01 1.2476306117578984E-01 1.2696048141762817E-01 1.2918972806927037E-01 1.3145122185131358E-01 1.3374538618897527E-01 1.3607264713739037E-01 1.3843343330180746E-01 1.4082817575252027E-01 1.4325730793436514E-01 1.4572126557060969E-01 1.4822048656105399E-01 1.5075541087415997E-01 1.5332648043301936E-01 1.5593413899496669E-01 1.5857883202463716E-01 1.6126100656026601E-01 1.6398111107301830E-01 1.6673959531913710E-01 1.6953691018468658E-01 1.7237350752267019E-01 1.7524983998228860E-01 1.7816636083010703E-01 1.8112352376288876E-01 1.8412178271185101E-01 1.8716159163809359E-01 1.9024340431894216E-01 1.9336767412495037E-01 1.9653485378729135E-01 1.9974539515527209E-01 2.0299974894369313E-01 2.0629836446977612E-01 2.0964168937937377E-01 2.1303016936217509E-01 2.1646424785561028E-01 2.1994436573716164E-01 2.2347096100477565E-01 2.2704446844507215E-01 2.3066531928904310E-01 2.3433394085492432E-01 2.3805075617792859E-01 2.4181618362651591E-01 2.4563063650488420E-01 2.4949452264134955E-01 2.5340824396229394E-01 2.5737219605134765E-01 2.6138676769347763E-01 2.6545234040364774E-01 2.6956928793971802E-01 2.7373797579925113E-01 2.7795876069988756E-01 2.8223199004296168E-01 2.8655800136002035E-01 2.9093712174191733E-01 2.9536966725015107E-01 2.9985594231012080E-01 3.0439623908597685E-01 3.0899083683674433E-01 3.1364000125340930E-01 3.1834398377665085E-01 3.2310302089492288E-01 3.2791733342258361E-01 3.3278712575778702E-01 3.3771258511985508E-01 3.4269388076586199E-01 3.4773116318616892E-01 3.5282456327866479E-01 3.5797419150147630E-01 3.6318013700392721E-01 3.6844246673554515E-01 3.7376122453292204E-01 3.7913643018426546E-01 3.8456807847148222E-01 3.9005613818967433E-01 3.9560055114392839E-01 4.0120123112332756E-01 4.0685806285211878E-01 4.1257090091801207E-01 4.1833956867760719E-01 4.2416385713897953E-01 4.3004352382148980E-01 4.3597829159291268E-01 4.4196784748402529E-01 4.4801184148082246E-01 4.5410988529458496E-01 4.6026155111004974E-01 4.6646637031199895E-01 4.7272383219061159E-01 4.7903338262599482E-01 4.8539442275234379E-01 4.9180630760225064E-01 4.9826834473173998E-01 5.0477979282665830E-01 5.1133986029113099E-01 5.1794770381884125E-01 5.2460242694798553E-01 5.3130307860080506E-01 5.3804865160869408E-01 5.4483808122394917E-01 5.5167024361931616E-01 5.5854395437657400E-01 5.6545796696548678E-01 5.7241097121454987E-01 5.7940159177504735E-01 5.8642838658005036E-01 5.9348984530007209E-01 6.0058438779722501E-01 6.0771036257981592E-01 6.1486604525944777E-01 6.2204963701279614E-01 6.2925926305037450E-01 6.3649297109470471E-01 6.4374872987045062E-01 6.5102442760920931E-01 6.5831787057177316E-01 6.6562678159083977E-01 6.7294879863726309E-01 6.8028147341310907E-01 6.8762226997490594E-01 6.9496856339065172E-01 7.0231763843427197E-01 7.0966668832140312E-01 7.1701281349050860E-01 7.2435302043351613E-01 7.3168422058031612E-01 7.3900322924161999E-01 7.4630676461485457E-01 7.5359144685791368E-01 7.6085379723577196E-01 7.6809023734510729E-01 7.7529708842226175E-01 7.8247057074001281E-01 7.8960680309879105E-01 7.9670180241814537E-01 8.0375148343438396E-01 8.1075165851049580E-01 8.1769803756457138E-01 8.2458622812309346E-01 8.3141173550560410E-01 8.3816996314735293E-01 8.4485621306667302E-01 8.5146568648391763E-01 8.5799348459890779E-01 8.6443460953390605E-01 8.7078396544922887E-01 8.7703635983867534E-01 8.8318650501199225E-01 8.8922901977168090E-01 8.9515843129143213E-01 9.0096917720356584E-01 9.0665560790281963E-01 9.1221198907387713E-01 9.1763250444999767E-01 9.2291125881012248E-01 9.2804228122181243E-01 9.3301952853733361E-01 9.3783688915020436E-01 9.4248818701943660E-01 9.4696718596867246E-01 9.5126759426733087E-01 9.5538306950077623E-01 9.5930722373636845E-01 9.6303362899207601E-01 9.6655582301405929E-01 9.6986731536926130E-01 9.7296159385858072E-01 9.7583213125550783E-01 9.7847239237427719E-01 9.8087584147043227E-01 9.8303594997529120E-01 9.8494620456393600E-01 9.8660011555414862E-01 9.8799122563096231E-01 9.8911311888830566E-01 9.8995943017549060E-01 9.9052385473216986E-01 9.9080015809093946E-01 9.9078218622216974E-01 9.9046387589127416E-01 9.8983926519471777E-01 9.8890250423824599E-01 9.8764786591944564E-01 9.8606975677749553E-01 9.8416272787616954E-01 9.8192148569229598E-01 9.7934090299093912E-01 9.7641602968040242E-01 9.7314210365418363E-01 9.6951456164227767E-01 9.6552905010952084E-01 9.6118143625249464E-01 9.5646781915750967E-01 9.5138454118895743E-01 9.4592819967904784E-01 9.4009565898604852E-01 9.3388406297859017E-01 9.2729084798869710E-01 9.2031375625663303E-01 9.1295084986712782E-01 9.0520052515013338E-01 8.9706152749116097E-01 8.8853296646803759E-01 8.7961433120470944E-01 8.7030550581074062E-01 8.6060678475989250E-01 8.5051888805434384E-01 8.4004297602369371E-01 8.2918066361921461E-01 8.1793403408204968E-01 8.0630565188623426E-01 7.9429857488023037E-01 7.8191636557125066E-01 7.6916310151284772E-01 7.5604338476722088E-01 7.4256235041950813E-01 7.2872567412301026E-01 7.1453957865309070E-01 7.0001083944486553E-01 6.8514678908690108E-01 6.6995532074077213E-01 6.5444489045502341E-01 6.3862451834188327E-01 6.2250378858595667E-01 6.0609284825578569E-01 5.8940240489138995E-01 5.7244372284335898E-01 5.5522861834159543E-01 5.3776945327419778E-01 5.2007912765920350E-01 5.0217107079389289E-01 4.8405923106812287E-01 4.6575806442976259E-01 4.4728252149174219E-01 4.2864803327163359E-01 4.0987049555604360E-01 3.9096625188352846E-01 3.7195207514125073E-01 3.5284514777229187E-01 3.3366304059242047E-01 3.1442369021728500E-01 2.9514537510350547E-01 2.7584669021002373E-01 2.5654652028945013E-01 2.3726401182302587E-01 2.1801854361732909E-01 1.9882969608599552E-01 1.7971721924560466E-01 1.6070099946146746E-01 1.4180102498638891E-01 1.2303735034347042E-01 1.0443005961258429E-01 8.5999228689087132E-02 6.7764886592370038E-02 4.9746975910597131E-02 3.1965312475973701E-02 1.4439544371552085E-02 -2.8108896247070869E-03 -1.9766802050767029E-02 -3.6409299119348974E-02 -5.2719823322182897E-02 -6.8680196184520745E-02 -8.4272661084327169E-02 -9.9479926060172641E-02 -1.1428520653790958E-01 -1.2867226790327907E-01 -1.4262546782820909E-01 -1.5612979821349512E-01 -1.6917092652975618E-01 -1.8173523621349613E-01 -1.9380986560238522E-01 -2.0538274468069614E-01 -2.1644262867621375E-01 -2.2697912734934536E-01 -2.3698272871120474E-01 -2.4644481598187432E-01 -2.5535767693114708E-01 -2.6371450538321867E-01 -2.7150939560922466E-01 -2.7873733149541674E-01 -2.8539417358503727E-01 -2.9147664806751133E-01 -2.9698234215988384E-01 -3.0190970970969500E-01 -3.0625808903292101E-01 -3.1002773218818802E-01 -3.1321984182068763E-01 -3.1583660946389780E-01 -3.1788124865189510E-01 -3.1935801754301574E-01 -3.2027222832787716E-01 -3.2063024339932078E-01 -3.2043946019059133E-01 -3.1970828740760115E-01 -3.1844611529187145E-01 -3.1666328197716603E-01 -3.1437103731150151E-01 -3.1158150491087772E-01 -3.0830764276167338E-01 -3.0456320239520446E-01 -3.0036268649582359E-01 -2.9572130474410346E-01 -2.9065492771194967E-01 -2.8518003869237118E-01 -2.7931368344135982E-01 -2.7307341791424733E-01 -2.6647725417943413E-01 -2.5954360477846267E-01 -2.5229122586746100E-01 -2.4473915951936256E-01 -2.3690667559011949E-01 -2.2881321355823492E-01 -2.2047832473890300E-01 -2.1192161525549724E-01 -2.0316269012527721E-01 -1.9422109878562446E-01 -1.8511628235389246E-01 -1.7586752287950069E-01 -1.6649389481227428E-01 -1.5701421887689718E-01 -1.4744701851020939E-01 -1.3781047898623572E-01 -1.2812240932355534E-01 -1.1840020704106360E-01 -1.0866082580152030E-01 -9.8920745957630882E-02 -8.9195947992913346E-02 -7.9501888829334122E-02 -6.9853480955739858E-02 -6.0265074315510161E-02 -5.0750440878612156E-02 -4.1322761812333089E-02 -3.1994617156322187E-02 -2.2777977901079070E-02 -1.3684200364518156E-02 -4.7240227585181056E-03 4.0924361638178660E-03 1.2755676489387099E-02 2.1256814662967166E-02 2.9587579248258090E-02 3.7740305036644703E-02 4.5707925606280578E-02 5.3483964432441695E-02 6.1062524648968095E-02 6.8438277560093658E-02 7.5606450002220715E-02 8.2562810656041152E-02 8.9303655410736649E-02 9.5825791883492412E-02 1.0212652319872688E-01 1.0820363113189142E-01 1.1405535872174004E-01 1.1968039245214021E-01 1.2507784409927589E-01 1.3024723233211818E-01 1.3518846414325672E-01 1.3990181617375846E-01 1.4438791598027936E-01 1.4864772327620923E-01 1.5268251116265341E-01 1.5649384735141519E-01 1.6008357537294296E-01 1.6345379575964300E-01 1.6660684720093102E-01 1.6954528768222449E-01 1.7227187564601032E-01 1.7478955124808332E-01 1.7710141782331873E-01 1.7921072371866373E-01 1.8112084469091222E-01 1.8283526709718875E-01 1.8435757212122345E-01 1.8569142127413851E-01 1.8684054338261813E-01 1.8780872323092782E-01 1.8859979196019969E-01 1.8921761925504413E-01 1.8966610727167188E-01 1.8994918619124848E-01 1.9007081122395356E-01 1.9003496084792609E-01 1.8984563604503907E-01 1.8950686029188690E-01 1.8902268007689921E-01 1.8839716573923673E-01 1.8763441245756510E-01 1.8673854125257405E-01 1.8571369990245420E-01 1.8456406370262635E-01 1.8329383602791355E-01 1.8190724867609118E-01 1.8040856198596739E-01 1.7880206473107138E-01 1.7709207379212491E-01 1.7528293360843827E-01 1.7337901540096476E-01 1.7138471614877668E-01 1.6930445728706109E-01 1.6714268307928878E-01 1.6490385860007506E-01 1.6259246724959278E-01 1.6021300770663036E-01 1.5776999021702748E-01 1.5526793210892922E-01 1.5271135242769240E-01 1.5010476559284031E-01 1.4745267399830012E-01 1.4475955950579125E-01 1.4202987381946242E-01 1.3926802777653086E-01 1.3647837964169907E-01 1.3366522254954399E-01 1.3083277129527882E-01 1.2798514872632097E-01 1.2512637203100996E-01 1.2226033925336993E-01 1.1939081638113666E-01 1.1652142535604668E-01 1.1365563334391250E-01 1.1079674357116762E-01 1.0794788799415521E-01 1.0511202201458958E-01 1.0229192139231821E-01 9.9490181442808079E-02 9.6709218537561009E-02 9.3951273859004467E-02 9.1218419296502373E-02 8.8512565309707747E-02 8.5835470530623001E-02 8.3188752827539111E-02 8.0573901513421115E-02 7.7992290349201174E-02 7.5445190969781403E-02 7.2933786348361479E-02 7.0459183913997317E-02 6.8022427949004871E-02 6.5624510917542553E-02 6.3266383414575494E-02 6.0948962474857968E-02 5.8673138043141927E-02 5.6439777477195391E-02 5.4249728031220329E-02 5.2103817345061337E-02 5.0002852037107616E-02 4.7947614577572135E-02 4.5938858669734718E-02 4.3977303404095600E-02 4.2063626497944970E-02 4.0198456937941329E-02 3.8382367344762518E-02 3.6615866364629747E-02 3.4899391366611271E-02 3.3233301689798989E-02 3.1617872643610587E-02 3.0053290420445241E-02 2.8539648035283187E-02 2.7076942363733786E-02 2.5665072310190828E-02 2.4303838102338420E-02 2.2992941677992824E-02 2.1731988105479078E-02 2.0520487959415964E-02 1.9357860559644842E-02 1.8243437971645137E-02 1.7176469661575416E-02 1.6156127697455600E-02 1.5181512389347143E-02 1.4251658265096431E-02 1.3365540283736101E-02 1.2522080195491342E-02 1.1720152965091324E-02 1.0958593183370060E-02 1.0236201400660264E-02 9.5517503239931061E-03 8.9039908284276117E-03 8.2916577408013951E-03 7.7134753617143963E-03 7.1681626985583349E-03 6.6544383888402364E-03 6.1710252988980844E-03 5.7166547883627803E-03 5.2900706353919335E-03 4.8900326218059946E-03 4.5153197808203201E-03 4.1647333131197145E-03 3.8370991795980652E-03 3.5312703812218605E-03 3.2461289382087928E-03 2.9805875820794110E-03 2.7335911751765079E-03 2.5041178729894925E-03 2.2911800451030895E-03 2.0938249708435351E-03 1.9111353257512170E-03 1.7422294748948100E-03 1.5862615887841222E-03 1.4424215972617400E-03 1.3099349962784525E-03 1.1880625219046110E-03 1.0760997053166881E-03 9.7337632184131854E-04 8.7925574645195364E-04 7.9313422740828017E-04 7.1444008901624890E-04 6.4263287377584613E-04 5.7720243348228888E-04 5.1766797816015051E-04 4.6357709104403419E-04 4.1450471717762463E-04 3.7005213258806238E-04 3.2984590040657260E-04 2.9353681975026843E-04 2.6079887265462881E-04 2.3132817385117699E-04 2.0484192771998123E-04 1.8107739631080847E-04 1.5979088191900157E-04 1.4075672732106421E-04 1.2376633641905725E-04 1.0862721771069152E-04 9.5162052691887008E-05 8.3207791009024386E-05 7.2614773907655686E-05 6.3245887271709143E-05 5.4975745310923161E-05 4.7689905733249439E-05 4.1284117032259378E-05 3.5663598326299436E-05 3.0742352005533830E-05 2.6442509274474570E-05 2.2693708520640925E-05 1.9432506294219182E-05 1.6601820548722369E-05 1.4150405668445527E-05 1.2032358694817547E-05 1.0206656060437659E-05 8.6367200465534419E-06 7.2900140968969003E-06 6.1376660480466565E-06 5.1541182737131713E-06 4.3168036874026408E-06 3.6058465046221440E-06 3.0037866319126783E-06 2.4953265252600336E-06 2.0670993445037837E-06 1.7074572228571368E-06 1.4062784711277134E-06 1.1547925442053468E-06 9.4542161232630105E-07 7.7163760096404851E-07 6.2783359033212673E-07 5.0920849778743491E-07 4.1166400324874931E-07 3.3171271844286245E-07 2.6639664470768206E-07 2.1321501057418453E-07 1.7006062879023198E-07 1.3516396223548686E-07 1.0704413873519367E-07 8.4466205574861474E-08 6.6403965052683473E-08 5.2007782231921798E-08 4.0576804769751286E-08 3.1535081950629524E-08 2.4411115540655790E-08 1.8820418555151435E-08 1.4450699295484308E-08 1.1049326911994910E-08 8.4127711826691456E-09 6.3777430997046941E-09 4.8137942053819711E-09 3.6171614270935780E-09 2.7056704726247719E-09 2.0145347313119873E-09 1.4929081775711394E-09 1.1010701018262639E-09 8.0813672550859361E-10 5.9021002716866540E-10 4.2888755866751480E-10 3.1006880884288446E-10 2.2300392296351056E-10 1.5953945894609691E-10 1.1352348370074021E-10 8.0338824916362919E-11 5.6538867961266627E-11 3.9564902693339593E-11 2.7527915689032386E-11 1.9041325030614325E-11 1.3093263289573203E-11 8.9491936930460932E-12 6.0797932311886440E-12 4.1060562278369684E-12 2.7558246957559263E-12 1.8376203723558148E-12 1.2172771909108252E-12 8.0094703283213493E-13 </ae_partial_wave> <pseudo_partial_wave state= "Ni3" grid="log1"> 1.4014253963572955E-13 1.6705054680497198E-06 3.3694411108703735E-06 5.0972907787407105E-06 6.8545465565262549E-06 8.6417089038218384E-06 1.0459286797479419E-05 1.2307797876561208E-05 1.4187768589759907E-05 1.6099734345327666E-05 1.8044239663556611E-05 2.0021838331854420E-05 2.2033093562458969E-05 2.4078578152837019E-05 2.6158874648812669E-05 2.8274575510471931E-05 3.0426283280890759E-05 3.2614610757734423E-05 3.4840181167777501E-05 3.7103628344393430E-05 3.9405596908064995E-05 4.1746742449966690E-05 4.4127731718671154E-05 4.6549242810033138E-05 4.9011965360304941E-05 5.1516600742538132E-05 5.4063862266327974E-05 5.6654475380956635E-05 5.9289177881993851E-05 6.1968720121413428E-05 6.4693865221285269E-05 6.7465389291104268E-05 7.0284081648817502E-05 7.3150745045612840E-05 7.6066195894532854E-05 7.9031264502979438E-05 8.2046795309174874E-05 8.5113647122647064E-05 8.8232693368806901E-05 9.1404822337688376E-05 9.4630937436920916E-05 9.7911957449006883E-05 1.0124881679297759E-04 1.0464246579050131E-04 1.0809387093652060E-04 1.1160401517449401E-04 1.1517389817632260E-04 1.1880453662703936E-04 1.2249696451434343E-04 1.2625223342306119E-04 1.3007141283461821E-04 1.3395559043160714E-04 1.3790587240753832E-04 1.4192338378186153E-04 1.4600926872034798E-04 1.5016469086092415E-04 1.5439083364505025E-04 1.5868890065473732E-04 1.6306011595529905E-04 1.6750572444393619E-04 1.7202699220425185E-04 1.7662520686679965E-04 1.8130167797576698E-04 1.8605773736189664E-04 1.9089473952175548E-04 1.9581406200345477E-04 2.0081710579893466E-04 2.0590529574292352E-04 2.1108008091868480E-04 2.1634293507066799E-04 2.2169535702418135E-04 2.2713887111220350E-04 2.3267502760945867E-04 2.3830540317387692E-04 2.4403160129556428E-04 2.4985525275341303E-04 2.5577801607948000E-04 2.6180157803126552E-04 2.6792765407202728E-04 2.7415798885926647E-04 2.8049435674152348E-04 2.8693856226362610E-04 2.9349244068053347E-04 3.0015785847992078E-04 3.0693671391365508E-04 3.1383093753831160E-04 3.2084249276488630E-04 3.2797337641785800E-04 3.3522561930376173E-04 3.4260128678943448E-04 3.5010247939009601E-04 3.5773133336743334E-04 3.6549002133785856E-04 3.7338075289111320E-04 3.8140577521939418E-04 3.8956737375717956E-04 3.9786787283193877E-04 4.0630963632590884E-04 4.1489506834912489E-04 4.2362661392389970E-04 4.3250675968094210E-04 4.4153803456731451E-04 4.5072301056642999E-04 4.6006430343029352E-04 4.6956457342419442E-04 4.7922652608406349E-04 4.8905291298670633E-04 4.9904653253313516E-04 5.0921023074521879E-04 5.1954690207587739E-04 5.3005949023305428E-04 5.4075098901769283E-04 5.5162444317596285E-04 5.6268294926597334E-04 5.7392965653921919E-04 5.8536776783701125E-04 5.9700054050214541E-04 6.0883128730606446E-04 6.2086337739178257E-04 6.3310023723283249E-04 6.4554535160851257E-04 6.5820226459570351E-04 6.7107458057754515E-04 6.8416596526924640E-04 6.9748014676133344E-04 7.1102091658061287E-04 7.2479213076917211E-04 7.3879771098169921E-04 7.5304164560145302E-04 7.6752799087518274E-04 7.8226087206732613E-04 7.9724448463381605E-04 8.1248309541581286E-04 8.2798104385371578E-04 8.4374274322178422E-04 8.5977268188372534E-04 8.7607542456959349E-04 8.9265561367437402E-04 9.0951797057860163E-04 9.2666729699140353E-04 9.4410847631632387E-04 9.6184647504034043E-04 9.7988634414643955E-04 9.9823322055016326E-04 1.0168923285605242E-03 1.0358689813657019E-03 1.0551685825439436E-03 1.0747966276000781E-03 1.0947587055280933E-03 1.1150605004002000E-03 1.1357077929828405E-03 1.1567064623800817E-03 1.1780624877048662E-03 1.1997819497785826E-03 1.2218710328594227E-03 1.2443360264000314E-03 1.2671833268349127E-03 1.2904194393981178E-03 1.3140509799716936E-03 1.3380846769654410E-03 1.3625273732284740E-03 1.3873860279931315E-03 1.4126677188517863E-03 1.4383796437670759E-03 1.4645291231161458E-03 1.4911236017694446E-03 1.5181706512046734E-03 1.5456779716564422E-03 1.5736533943022705E-03 1.6021048834854929E-03 1.6310405389757159E-03 1.6604685982674352E-03 1.6903974389174481E-03 1.7208355809217085E-03 1.7517916891322712E-03 1.7832745757149998E-03 1.8152932026486994E-03 1.8478566842663701E-03 1.8809742898392660E-03 1.9146554462044776E-03 1.9489097404367397E-03 1.9837469225652080E-03 2.0191769083359257E-03 2.0552097820207465E-03 2.0918557992734674E-03 2.1291253900339361E-03 2.1670291614809367E-03 2.2055779010346234E-03 2.2447825794093420E-03 2.2846543537176200E-03 2.3252045706261952E-03 2.3664447695648928E-03 2.4083866859892361E-03 2.4510422546976294E-03 2.4944236132040162E-03 2.5385431051669020E-03 2.5834132838756267E-03 2.6290469157948357E-03 2.6754569841680440E-03 2.7226566926812886E-03 2.7706594691877468E-03 2.8194789694943830E-03 2.8691290812115147E-03 2.9196239276663696E-03 2.9709778718815779E-03 3.0232055206196704E-03 3.0763217284945810E-03 3.1303416021512130E-03 3.1852805045141357E-03 3.2411540591064615E-03 3.2979781544400224E-03 3.3557689484778911E-03 3.4145428731704327E-03 3.4743166390659125E-03 3.5351072399969004E-03 3.5969319578435239E-03 3.6598083673747986E-03 3.7237543411691790E-03 3.7887880546154970E-03 3.8549279909955341E-03 3.9221929466493662E-03 3.9906020362247630E-03 4.0601746980118278E-03 4.1309306993641262E-03 4.2028901422075668E-03 4.2760734686382827E-03 4.3505014666107610E-03 4.4261952757175373E-03 4.5031763930617188E-03 4.5814666792236055E-03 4.6610883643227654E-03 4.7420640541768061E-03 4.8244167365582066E-03 4.9081697875504853E-03 4.9933469780050659E-03 5.0799724801001249E-03 5.1680708740027646E-03 5.2576671546358663E-03 5.3487867385508901E-03 5.4414554709080179E-03 5.5356996325649039E-03 5.6315459472753961E-03 5.7290215889995531E-03 5.8281541893261879E-03 5.9289718450093679E-03 6.0315031256200401E-03 6.1357770813141805E-03 6.2418232507186035E-03 6.3496716689358081E-03 6.4593528756690414E-03 6.5708979234687815E-03 6.6843383861018889E-03 6.7997063670445033E-03 6.9170345080999292E-03 7.0363559981425784E-03 7.1577045819890290E-03 7.2811145693972620E-03 7.4066208441950672E-03 7.5342588735386089E-03 7.6640647173020033E-03 7.7960750375988446E-03 7.9303271084363424E-03 8.0668588255030128E-03 8.2057087160904013E-03 8.3469159491495887E-03 8.4905203454828885E-03 8.6365623880712821E-03 8.7850832325379064E-03 8.9361247177478457E-03 9.0897293765444271E-03 9.2459404466220009E-03 9.4048018815352796E-03 9.5663583618448827E-03 9.7306553063989647E-03 9.8977388837502202E-03 1.0067656023707929E-02 1.0240454429024092E-02 1.0416182587212794E-02 1.0594889782501626E-02 1.0776626107913936E-02 1.0961442477480337E-02 1.1149390638577695E-02 1.1340523184393849E-02 1.1534893566515473E-02 1.1732556107637073E-02 1.1933566014387945E-02 1.2137979390274485E-02 1.2345853248734037E-02 1.2557245526297084E-02 1.2772215095853429E-02 1.2990821780018145E-02 1.3213126364592506E-02 1.3439190612114644E-02 1.3669077275494433E-02 1.3902850111726492E-02 1.4140573895674738E-02 1.4382314433921404E-02 1.4628138578672987E-02 1.4878114241714950E-02 1.5132310408406407E-02 1.5390797151705243E-02 1.5653645646213899E-02 1.5920928182234752E-02 1.6192718179823776E-02 1.6469090202830109E-02 1.6750119972908286E-02 1.7035884383489457E-02 1.7326461513696292E-02 1.7621930642186114E-02 1.7922372260904956E-02 1.8227868088734934E-02 1.8538501085015712E-02 1.8854355462919786E-02 1.9175516702660208E-02 1.9502071564507738E-02 1.9834108101593532E-02 2.0171715672471446E-02 2.0514984953413178E-02 2.0864007950407017E-02 2.1218878010830357E-02 2.1579689834763400E-02 2.1946539485910223E-02 2.2319524402091340E-02 2.2698743405269426E-02 2.3084296711068601E-02 2.3476285937744541E-02 2.3874814114561028E-02 2.4279985689525350E-02 2.4691906536433373E-02 2.5110683961171502E-02 2.5536426707220453E-02 2.5969244960302378E-02 2.6409250352110503E-02 2.6856555963056181E-02 2.7311276323965822E-02 2.7773527416656139E-02 2.8243426673312141E-02 2.8721092974589385E-02 2.9206646646356867E-02 2.9700209454993517E-02 3.0201904601146051E-02 3.0711856711852403E-02 3.1230191830928990E-02 3.1757037407515794E-02 3.2292522282667963E-02 3.2836776673876397E-02 3.3389932157395608E-02 3.3952121648249546E-02 3.4523479377781358E-02 3.5104140868605332E-02 3.5694242906814146E-02 3.6293923511286137E-02 3.6903321899931313E-02 3.7522578452706408E-02 3.8151834671222573E-02 3.8791233134760517E-02 3.9440917452500016E-02 4.0101032211762255E-02 4.0771722922053867E-02 4.1453135954693944E-02 4.2145418477793975E-02 4.2848718386353006E-02 4.3563184227217874E-02 4.4288965118650825E-02 4.5026210664234227E-02 4.5775070860831907E-02 4.6535696000316248E-02 4.7308236564757175E-02 4.8092843114759705E-02 4.8889666170623042E-02 4.9698856085983525E-02 5.0520562913590271E-02 5.1354936262851439E-02 5.2202125148775251E-02 5.3062277831918164E-02 5.3935541648938962E-02 5.4822062833346320E-02 5.5721986326012760E-02 5.6635455575017278E-02 5.7562612324364999E-02 5.8503596391119871E-02 5.9458545430476212E-02 6.0427594688280621E-02 6.1410876740506513E-02 6.2408521219171204E-02 6.3420654524177292E-02 6.4447399520548371E-02 6.5488875220522394E-02 6.6545196449957364E-02 6.7616473498498156E-02 6.8702811752947790E-02 6.9804311313283268E-02 7.0921066590753340E-02 7.2053165887495566E-02 7.3200690957112916E-02 7.4363716545652353E-02 7.5542309912435809E-02 7.6736530330203737E-02 7.7946428564041048E-02 7.9172046328575330E-02 8.0413415722952505E-02 8.1670558643120117E-02 8.2943486170975966E-02 8.4232197939971470E-02 8.5536681476795717E-02 8.6856911518809587E-02 8.8192849306945140E-02 8.9544441853842124E-02 9.0911621187051816E-02 9.2294303567205818E-02 9.3692388681123326E-02 9.5105758809909444E-02 9.6534277972190857E-02 9.7977791042729342E-02 9.9436122846763730E-02 1.0090907723054311E-01 1.0239643610864232E-01 1.0389795848878186E-01 1.0541337947501911E-01 1.0694240925033040E-01 1.0848473203976425E-01 1.1004000505552060E-01 1.1160785742548671E-01 1.1318788910695374E-01 1.1477966978742926E-01 1.1638273777467055E-01 1.1799659887826665E-01 1.1962072528531634E-01 1.2125455443296164E-01 1.2289748788075885E-01 1.2454889018608245E-01 1.2620808778597178E-01 1.2787436788903694E-01 1.2954697738123389E-01 1.3122512174950149E-01 1.3290796402741395E-01 1.3459462376713946E-01 1.3628417604210066E-01 1.3797565048480528E-01 1.3966803036433828E-01 1.4136025170798011E-01 1.4305120247132977E-01 1.4473972176114952E-01 1.4642459911491346E-01 1.4810457384070863E-01 1.4977833442070307E-01 1.5144451798084710E-01 1.5310170982879506E-01 1.5474844306121477E-01 1.5638319824067659E-01 1.5800440314116893E-01 1.5961043255996415E-01 1.6119960819203372E-01 1.6277019856148672E-01 1.6432041900256192E-01 1.6584843168053270E-01 1.6735234564048579E-01 1.6883021686930130E-01 1.7028004835330088E-01 1.7169979011093939E-01 1.7308733917662719E-01 1.7444053950828359E-01 1.7575718178758387E-01 1.7703500307811459E-01 1.7827168630283163E-01 1.7946485949842214E-01 1.8061209480045415E-01 1.8171090710968882E-01 1.8275875238674014E-01 1.8375302551954131E-01 1.8469105770599181E-01 1.8557011329291101E-01 1.8638738601223442E-01 1.8713999455651906E-01 1.8782497743855694E-01 1.8843928708454613E-01 1.8897978311719138E-01 1.8944322479466397E-01 1.8982626258395752E-01 1.9012542886324682E-01 1.9033712776782347E-01 1.9045762421849821E-01 1.9048303220044591E-01 1.9040930239474696E-01 1.9023220930472240E-01 1.8994733806487621E-01 1.8955007117208195E-01 1.8903557543667615E-01 1.8839878951531552E-01 1.8763441245756510E-01 1.8673854125257405E-01 1.8571369990245420E-01 1.8456406370262635E-01 1.8329383602791355E-01 1.8190724867609118E-01 1.8040856198596739E-01 1.7880206473107138E-01 1.7709207379212491E-01 1.7528293360843827E-01 1.7337901540096476E-01 1.7138471614877668E-01 1.6930445728706109E-01 1.6714268307928878E-01 1.6490385860007506E-01 1.6259246724959278E-01 1.6021300770663036E-01 1.5776999021702748E-01 1.5526793210892922E-01 1.5271135242769240E-01 1.5010476559284031E-01 1.4745267399830012E-01 1.4475955950579125E-01 1.4202987381946242E-01 1.3926802777653086E-01 1.3647837964169907E-01 1.3366522254954399E-01 1.3083277129527882E-01 1.2798514872632097E-01 1.2512637203100996E-01 1.2226033925336993E-01 1.1939081638113666E-01 1.1652142535604668E-01 1.1365563334391250E-01 1.1079674357116762E-01 1.0794788799415521E-01 1.0511202201458958E-01 1.0229192139231821E-01 9.9490181442808079E-02 9.6709218537561009E-02 9.3951273859004467E-02 9.1218419296502373E-02 8.8512565309707747E-02 8.5835470530623001E-02 8.3188752827539111E-02 8.0573901513421115E-02 7.7992290349201174E-02 7.5445190969781403E-02 7.2933786348361479E-02 7.0459183913997317E-02 6.8022427949004871E-02 6.5624510917542553E-02 6.3266383414575494E-02 6.0948962474857968E-02 5.8673138043141927E-02 5.6439777477195391E-02 5.4249728031220329E-02 5.2103817345061337E-02 5.0002852037107616E-02 4.7947614577572135E-02 4.5938858669734718E-02 4.3977303404095600E-02 4.2063626497944970E-02 4.0198456937941329E-02 3.8382367344762518E-02 3.6615866364629747E-02 3.4899391366611271E-02 3.3233301689798989E-02 3.1617872643610587E-02 3.0053290420445241E-02 2.8539648035283187E-02 2.7076942363733786E-02 2.5665072310190828E-02 2.4303838102338420E-02 2.2992941677992824E-02 2.1731988105479078E-02 2.0520487959415964E-02 1.9357860559644842E-02 1.8243437971645137E-02 1.7176469661575416E-02 1.6156127697455600E-02 1.5181512389347143E-02 1.4251658265096431E-02 1.3365540283736101E-02 1.2522080195491342E-02 1.1720152965091324E-02 1.0958593183370060E-02 1.0236201400660264E-02 9.5517503239931061E-03 8.9039908284276117E-03 8.2916577408013951E-03 7.7134753617143963E-03 7.1681626985583349E-03 6.6544383888402364E-03 6.1710252988980844E-03 5.7166547883627803E-03 5.2900706353919335E-03 4.8900326218059946E-03 4.5153197808203201E-03 4.1647333131197145E-03 3.8370991795980652E-03 3.5312703812218605E-03 3.2461289382087928E-03 2.9805875820794110E-03 2.7335911751765079E-03 2.5041178729894925E-03 2.2911800451030895E-03 2.0938249708435351E-03 1.9111353257512170E-03 1.7422294748948100E-03 1.5862615887841222E-03 1.4424215972617400E-03 1.3099349962784525E-03 1.1880625219046110E-03 1.0760997053166881E-03 9.7337632184131854E-04 8.7925574645195364E-04 7.9313422740828017E-04 7.1444008901624890E-04 6.4263287377584613E-04 5.7720243348228888E-04 5.1766797816015051E-04 4.6357709104403419E-04 4.1450471717762463E-04 3.7005213258806238E-04 3.2984590040657260E-04 2.9353681975026843E-04 2.6079887265462881E-04 2.3132817385117699E-04 2.0484192771998123E-04 1.8107739631080847E-04 1.5979088191900157E-04 1.4075672732106421E-04 1.2376633641905725E-04 1.0862721771069152E-04 9.5162052691887008E-05 8.3207791009024386E-05 7.2614773907655686E-05 6.3245887271709143E-05 5.4975745310923161E-05 4.7689905733249439E-05 4.1284117032259378E-05 3.5663598326299436E-05 3.0742352005533830E-05 2.6442509274474570E-05 2.2693708520640925E-05 1.9432506294219182E-05 1.6601820548722369E-05 1.4150405668445527E-05 1.2032358694817547E-05 1.0206656060437659E-05 8.6367200465534419E-06 7.2900140968969003E-06 6.1376660480466565E-06 5.1541182737131713E-06 4.3168036874026408E-06 3.6058465046221440E-06 3.0037866319126783E-06 2.4953265252600336E-06 2.0670993445037837E-06 1.7074572228571368E-06 1.4062784711277134E-06 1.1547925442053468E-06 9.4542161232630105E-07 7.7163760096404851E-07 6.2783359033212673E-07 5.0920849778743491E-07 4.1166400324874931E-07 3.3171271844286245E-07 2.6639664470768206E-07 2.1321501057418453E-07 1.7006062879023198E-07 1.3516396223548686E-07 1.0704413873519367E-07 8.4466205574861474E-08 6.6403965052683473E-08 5.2007782231921798E-08 4.0576804769751286E-08 3.1535081950629524E-08 2.4411115540655790E-08 1.8820418555151435E-08 1.4450699295484308E-08 1.1049326911994910E-08 8.4127711826691456E-09 6.3777430997046941E-09 4.8137942053819711E-09 3.6171614270935780E-09 2.7056704726247719E-09 2.0145347313119873E-09 1.4929081775711394E-09 1.1010701018262639E-09 8.0813672550859361E-10 5.9021002716866540E-10 4.2888755866751480E-10 3.1006880884288446E-10 2.2300392296351056E-10 1.5953945894609691E-10 1.1352348370074021E-10 8.0338824916362919E-11 5.6538867961266627E-11 3.9564902693339593E-11 2.7527915689032386E-11 1.9041325030614325E-11 1.3093263289573203E-11 8.9491936930460932E-12 6.0797932311886440E-12 4.1060562278369684E-12 2.7558246957559263E-12 1.8376203723558148E-12 1.2172771909108252E-12 8.0094703283213493E-13 </pseudo_partial_wave> <projector_function state= "Ni3" grid="log1"> 5.6342420540287513E-10 7.3056662444209269E-05 1.4735652023506725E-04 2.2292096645960341E-04 2.9977139738230219E-04 3.7792977586930852E-04 4.5741832448661902E-04 5.3825965931370912E-04 6.2047685178227808E-04 7.0409327063375373E-04 7.8913276910128494E-04 8.7561952307436790E-04 9.6357820331271745E-04 1.0530338327503870E-03 1.1440119028666125E-03 1.2365383185800247E-03 1.3306394373403516E-03 1.4263420572027483E-03 1.5236734163834266E-03 1.6226612551468093E-03 1.7233337641297524E-03 1.8257196013722020E-03 1.9298479442350904E-03 2.0357484280736646E-03 2.1434512257159271E-03 2.2529870051519263E-03 2.3643869580350285E-03 2.4776828255748096E-03 2.5929068609057576E-03 2.7100918785061198E-03 2.8292712615196739E-03 2.9504789452479783E-03 3.0737494513814099E-03 3.1991178849178543E-03 3.3266199500257146E-03 3.4562919620302057E-03 3.5881708478401912E-03 3.7222941674254699E-03 3.8587001195620856E-03 3.9974275489942082E-03 4.1385159707494172E-03 4.2820055569534332E-03 4.4279371792031825E-03 4.5763523978855662E-03 4.7272934797980819E-03 4.8808034115849280E-03 5.0369259141192961E-03 5.1957054478158028E-03 5.3571872341262785E-03 5.5214172624201358E-03 5.6884423054586013E-03 5.8583099276251441E-03 6.0310685100874182E-03 6.2067672513401104E-03 6.3854561914472203E-03 6.5671862188451712E-03 6.7520090896984845E-03 6.9399774408790329E-03 7.1311448053473902E-03 7.3255656248791641E-03 7.5232952707280721E-03 7.7243900553659829E-03 7.9289072487847417E-03 8.1369050977943263E-03 8.3484428371938570E-03 8.5635807136284995E-03 8.7823799962336978E-03 9.0049029981921058E-03 9.2312130915697711E-03 9.4613747300146909E-03 9.6954534612775246E-03 9.9335159493854699E-03 1.0175629994164418E-02 1.0421864547962472E-02 1.0672289735648282E-02 1.0926976878221861E-02 1.1185998507875532E-02 1.1449428393369756E-02 1.1717341557635584E-02 1.1989814299960076E-02 1.2266924219080095E-02 1.2548750234345592E-02 1.2835372607484852E-02 1.3126872966565815E-02 1.3423334329211485E-02 1.3724841124885211E-02 1.4031479221004220E-02 1.4343335945165420E-02 1.4660500112056791E-02 1.4983062048509167E-02 1.5311113616324781E-02 1.5644748242823803E-02 1.5984060943533999E-02 1.6329148352298019E-02 1.6680108747023262E-02 1.7037042078158083E-02 1.7400049997666520E-02 1.7769235884990252E-02 1.8144704882634474E-02 1.8526563919996394E-02 1.8914921747195942E-02 1.9309888963942288E-02 1.9711578052967010E-02 2.0120103411472311E-02 2.0535581382836968E-02 2.0958130290591379E-02 2.1387870471895484E-02 2.1824924311884760E-02 2.2269416278300851E-02 2.2721472956699004E-02 2.3181223087927617E-02 2.3648797601943175E-02 2.4124329658678414E-02 2.4607954683123205E-02 2.5099810404242043E-02 2.5600036896760551E-02 2.6108776617093172E-02 2.6626174447357882E-02 2.7152377733543856E-02 2.7687536330707540E-02 2.8231802643244944E-02 2.8785331669145108E-02 2.9348281043750823E-02 2.9920811085463492E-02 3.0503084840150043E-02 3.1095268128621342E-02 3.1697529593401719E-02 3.2310040746568854E-02 3.2932976019075341E-02 3.3566512809683390E-02 3.4210831535904665E-02 3.4866115685586896E-02 3.5532551868628637E-02 3.6210329870663568E-02 3.6899642706215756E-02 3.7600686674394930E-02 3.8313661414188196E-02 3.9038769962400709E-02 3.9776218809985726E-02 4.0526217961433825E-02 4.1288980995056984E-02 4.2064725122829535E-02 4.2853671252464538E-02 4.3656044050993180E-02 4.4472072007720881E-02 4.5301987499874519E-02 4.6146026858455230E-02 4.7004430435363037E-02 4.7877442671774802E-02 4.8765312168517858E-02 4.9668291755186410E-02 5.0586638563963358E-02 5.1520614100964236E-02 5.2470484321677759E-02 5.3436519706824656E-02 5.4418995337859995E-02 5.5418190977220491E-02 5.6434391146118631E-02 5.7467885206684735E-02 5.8518967443032283E-02 5.9587937146247959E-02 6.0675098699215071E-02 6.1780761661514513E-02 6.2905240859976633E-02 6.4048856476304303E-02 6.5211934139134564E-02 6.6394805015363823E-02 6.7597805906314201E-02 6.8821279341089489E-02 7.0065573675551995E-02 7.1331043190799540E-02 7.2618048193758500E-02 7.3926955119441737E-02 7.5258136635615910E-02 7.6611971747769375E-02 7.7988845907926194E-02 7.9389151122711221E-02 8.0813286065800030E-02 8.2261656190797380E-02 8.3734673845988511E-02 8.5232758392048746E-02 8.6756336320533173E-02 8.8305841375121583E-02 8.9881714674839686E-02 9.1484404838852840E-02 9.3114368114402629E-02 9.4772068505342630E-02 9.6457977904768205E-02 9.8172576227940248E-02 9.9916351548805640E-02 1.0168980023863630E-01 1.0349342710592543E-01 1.0532774554037165E-01 1.0719327765759910E-01 1.0909055444783311E-01 1.1102011592570780E-01 1.1298251128332462E-01 1.1497829904608656E-01 1.1700804723063787E-01 1.1907233350515058E-01 1.2117174535401559E-01 1.2330688024265464E-01 1.2547834578748995E-01 1.2768675992737588E-01 1.2993275109849720E-01 1.3221695841158096E-01 1.3454003183317179E-01 1.3690263236859879E-01 1.3930543224911604E-01 1.4174911512147184E-01 1.4423437624070529E-01 1.4676192266675689E-01 1.4933247346348602E-01 1.5194675990176143E-01 1.5460552566510724E-01 1.5730952705998100E-01 1.6005953322783664E-01 1.6285632636262418E-01 1.6570070193020836E-01 1.6859346889245039E-01 1.7153544993471087E-01 1.7452748169692689E-01 1.7757041500851498E-01 1.8066511512767292E-01 1.8381246198382251E-01 1.8701335042453140E-01 1.9026869046651176E-01 1.9357940755030140E-01 1.9694644279947046E-01 2.0037075328430592E-01 2.0385331228891965E-01 2.0739510958352866E-01 2.1099715170093478E-01 2.1466046221723736E-01 2.1838608203741150E-01 2.2217506968522907E-01 2.2602850159799320E-01 2.2994747242606611E-01 2.3393309533705153E-01 2.3798650232495680E-01 2.4210884452413028E-01 2.4630129252851052E-01 2.5056503671547681E-01 2.5490128757537300E-01 2.5931127604563892E-01 2.6379625385079736E-01 2.6835749384734708E-01 2.7299629037403655E-01 2.7771395960797035E-01 2.8251183992588497E-01 2.8739129227097815E-01 2.9235370052580845E-01 2.9740047189031721E-01 3.0253303726610115E-01 3.0775285164617389E-01 3.1306139451088327E-01 3.1846017022950995E-01 3.2395070846809032E-01 3.2953456460303987E-01 3.3521332014119248E-01 3.4098858314565572E-01 3.4686198866804502E-01 3.5283519918696687E-01 3.5890990505261711E-01 3.6508782493784409E-01 3.7137070629554414E-01 3.7776032582227609E-01 3.8425848992840173E-01 3.9086703521465493E-01 3.9758782895497818E-01 4.0442276958604223E-01 4.1137378720288348E-01 4.1844284406117260E-01 4.2563193508589464E-01 4.3294308838628859E-01 4.4037836577726880E-01 4.4793986330707364E-01 4.5562971179114636E-01 4.6345007735236948E-01 4.7140316196716625E-01 4.7949120401794099E-01 4.8771647885113362E-01 4.9608129934129885E-01 5.0458801646070495E-01 5.1323901985455511E-01 5.2203673842151677E-01 5.3098364089929717E-01 5.4008223645526565E-01 5.4933507528165348E-01 5.5874474919521877E-01 5.6831389224092355E-01 5.7804518129955174E-01 5.8794133669844828E-01 5.9800512282555141E-01 6.0823934874573771E-01 6.1864686881944919E-01 6.2923058332259785E-01 6.3999343906775230E-01 6.5093843002532392E-01 6.6206859794460271E-01 6.7338703297361113E-01 6.8489687427700208E-01 6.9660131065112108E-01 7.0850358113530265E-01 7.2060697561829101E-01 7.3291483543865843E-01 7.4543055397799463E-01 7.5815757724557131E-01 7.7109940445285396E-01 7.8425958857650990E-01 7.9764173690802487E-01 8.1124951158817293E-01 8.2508663012433636E-01 8.3915686588840122E-01 8.5346404859303815E-01 8.6801206474377524E-01 8.8280485806403497E-01 8.9784642989034869E-01 9.1314083953439718E-01 9.2869220460852797E-01 9.4450470131096498E-01 9.6058256466673053E-01 9.7693008871989473E-01 9.9355162667246666E-01 1.0104515909649410E+00 1.0276344532929365E+00 1.0451047445541009E+00 1.0628670547189483E+00 1.0809260326187338E+00 1.0992863856430759E+00 1.1179528793391704E+00 1.1369303369043349E+00 1.1562236385623481E+00 1.1758377208138153E+00 1.1957775755497368E+00 1.2160482490168270E+00 1.2366548406220164E+00 1.2576025015629437E+00 1.2788964332697830E+00 1.3005418856431383E+00 1.3225441550711710E+00 1.3449085822080391E+00 1.3676405494944501E+00 1.3907454783993565E+00 1.4142288263607850E+00 1.4380960834015581E+00 1.4623527683943576E+00 1.4870044249483345E+00 1.5120566168876934E+00 1.5375149232903496E+00 1.5633849330523781E+00 1.5896722389418425E+00 1.6163824311023778E+00 1.6435210899647403E+00 1.6710937785209170E+00 1.6991060339128041E+00 1.7275633582834611E+00 1.7564712088359835E+00 1.7858349870406534E+00 1.8156600269274408E+00 1.8459515823963968E+00 1.8767148134740415E+00 1.9079547714391480E+00 1.9396763827362395E+00 1.9718844315898969E+00 2.0045835412274235E+00 2.0377781536116002E+00 2.0714725075792688E+00 2.1056706152751223E+00 2.1403762367635424E+00 2.1755928526944235E+00 2.2113236348920347E+00 2.2475714147286125E+00 2.2843386491368962E+00 2.3216273841083859E+00 2.3594392155161041E+00 2.3977752470931701E+00 2.4366360453903773E+00 2.4760215915283137E+00 2.5159312295519380E+00 2.5563636111878720E+00 2.5973166367977658E+00 2.6387873923140930E+00 2.6807720819387795E+00 2.7232659563794921E+00 2.7662632363939319E+00 2.8097570314090050E+00 2.8537392529797092E+00 2.8982005228519876E+00 2.9431300753952718E+00 2.9885156541740510E+00 3.0343434024339366E+00 3.0805977472869701E+00 3.1272612773935347E+00 3.1743146139547291E+00 3.2217362748502305E+00 3.2695025317826758E+00 3.3175872603215208E+00 3.3659617827775121E+00 3.4145947038844300E+00 3.4634517393181414E+00 3.5124955371453255E+00 3.5616854923663310E+00 3.6109775547994873E+00 3.6603240306488942E+00 3.7096733782051743E+00 3.7589699982502180E+00 3.8081540198735357E+00 3.8571610825605593E+00 3.9059221155833912E+00 3.9543631159130643E+00 4.0024049260801817E+00 4.0499630136393998E+00 4.0969472541424850E+00 4.1432617197962696E+00 4.1888044762752230E+00 4.2334673904746669E+00 4.2771359523286900E+00 4.3196891141768994E+00 4.3609991515445925E+00 4.4009315496003891E+00 4.4393449199715009E+00 4.4760909530263886E+00 4.5110144111740569E+00 4.5439531691731192E+00 4.5747383078869106E+00 4.6031942683551188E+00 4.6291390734703288E+00 4.6523846249384579E+00 4.6727370835550568E+00 4.6899973411310487E+00 4.7039615926376950E+00 4.7144220172949058E+00 4.7211675773820021E+00 4.7239849434857790E+00 4.7226595546970298E+00 4.7169768219007668E+00 4.7067234817541195E+00 4.6916891081852343E+00 4.6716677872511632E+00 4.6464599599377472E+00 4.6158744359449217E+00 4.5797305796515300E+00 4.5378606672708663E+00 4.4901124116686626E+00 4.4363516483964878E+00 4.3764651731750766E+00 4.3103637173223239E+00 4.2379850434395445E+00 4.1592971390246447E+00 4.0743014805475068E+00 3.9830363348716826E+00 3.8855800587008593E+00 3.7820543499224613E+00 3.6726273972549750E+00 3.5575168664066488E+00 3.4369926519308134E+00 3.3113793140117673E+00 3.1810581084168836E+00 3.0464685056848975E+00 2.9081090821801143E+00 2.7665376508600681E+00 2.6223704834932251E+00 2.4762804587747884E+00 2.3289939526942094E+00 2.1812862693047781E+00 2.0339753928995195E+00 1.8879138283150780E+00 1.7439782873287570E+00 1.6030569796475627E+00 1.4660342819606513E+00 1.3337725947636461E+00 1.2070912629658448E+00 1.0867425436937312E+00 9.7338476665943630E-01 8.6755306489989148E-01 7.6962837488325830E-01 6.7980583515954496E-01 5.9806427343341440E-01 5.2413918501599521E-01 4.5750249205273191E-01 3.9735345157576663E-01 3.4262636701200289E-01 2.9202226465852082E-01 2.4407343402402212E-01 1.9725171015479254E-01 1.5013361516431689E-01 1.0163800684096716E-01 5.1354753923132233E-02 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 </projector_function> <ae_partial_wave state= "Ni4" grid="log1"> -6.4844160272185922E-05 2.1801166466771947E-05 6.9248284504383321E-05 1.6948017595205998E-04 3.4511141368399905E-04 5.4938816133718313E-04 6.6895286271470317E-04 7.7790147761649020E-04 8.8221257528609963E-04 9.7703782706377363E-04 1.0690664943952114E-03 1.1590220218932426E-03 1.2474406897889445E-03 1.3349351121380666E-03 1.4218244150864365E-03 1.5083608182422750E-03 1.5947395646856359E-03 1.6811141295174255E-03 1.7676106548587148E-03 1.8543351360405449E-03 1.9413786329094500E-03 2.0288208620693532E-03 2.1167327286774102E-03 2.2051781756273555E-03 2.2942155599391476E-03 2.3838986988363700E-03 2.4742776795151850E-03 2.5653994963001155E-03 2.6573085594214828E-03 2.7500471066974892E-03 2.8436555406411860E-03 2.9381727074999689E-03 3.0336361304859872E-03 3.1300822064671903E-03 3.2275463731927618E-03 3.3260632525282698E-03 3.4256667739916893E-03 3.5263902819806770E-03 3.6282666293936928E-03 3.7313282598275704E-03 3.8356072801223411E-03 3.9411355247016208E-03 4.0479446128993332E-03 4.1560660002631635E-03 4.2655310246657819E-03 4.3763709479030218E-03 4.4886169933809590E-03 4.6023003803707776E-03 4.7174523552622515E-03 4.8341042201716583E-03 4.9522873592169961E-03 5.0720332627227985E-03 5.1933735495854052E-03 5.3163399880045287E-03 5.4409645147457794E-03 5.5672792530908066E-03 5.6953165296078469E-03 5.8251088898588921E-03 5.9566891131442798E-03 6.0900902263708884E-03 6.2253455171404157E-03 6.3624885461013303E-03 6.5015531586493655E-03 6.6425734960214589E-03 6.7855840058363140E-03 6.9306194521177719E-03 7.0777149248512370E-03 7.2269058490976755E-03 7.3782279936977987E-03 7.5317174796022271E-03 7.6874107878388657E-03 7.8453447671459845E-03 8.0055566412943219E-03 8.1680840161063618E-03 8.3329648861947721E-03 8.5002376414293982E-03 8.6699410731455023E-03 8.8421143801077021E-03 9.0167971742292283E-03 9.1940294860691982E-03 9.3738517700960207E-03 9.5563049097356374E-03 9.7414302222133039E-03 9.9292694631766317E-03 1.0119864831115983E-02 1.0313258971586796E-02 1.0509494981219177E-02 1.0708616411538396E-02 1.0910667272582816E-02 1.1115692036321246E-02 1.1323735639873871E-02 1.1534843488530608E-02 1.1749061458573861E-02 1.1966435899899531E-02 1.2187013638428088E-02 1.2410841978323223E-02 1.2637968703987371E-02 1.2868442081864979E-02 1.3102310862019967E-02 1.3339624279508367E-02 1.3580432055522644E-02 1.3824784398324267E-02 1.4072732003951011E-02 1.4324326056684994E-02 1.4579618229305456E-02 1.4838660683097943E-02 1.5101506067624325E-02 1.5368207520252291E-02 1.5638818665437114E-02 1.5913393613755732E-02 1.6191986960692795E-02 1.6474653785154319E-02 1.6761449647739877E-02 1.7052430588729479E-02 1.7347653125828699E-02 1.7647174251623713E-02 1.7951051430772299E-02 1.8259342596914016E-02 1.8572106149309840E-02 1.8889400949197690E-02 1.9211286315861813E-02 1.9537822022432764E-02 1.9869068291382727E-02 2.0205085789756771E-02 2.0545935624103430E-02 2.0891679335138386E-02 2.1242378892101392E-02 2.1598096686854331E-02 2.1958895527698846E-02 2.2324838632888942E-02 2.2695989623911214E-02 2.3072412518476360E-02 2.3454171723248089E-02 2.3841332026331805E-02 2.4233958589488819E-02 2.4632116940152056E-02 2.5035872963164420E-02 2.5445292892346434E-02 2.5860443301830294E-02 2.6281391097202355E-02 2.6708203506493507E-02 2.7140948070981545E-02 2.7579692635869926E-02 2.8024505340848820E-02 2.8475454610543016E-02 2.8932609144914009E-02 2.9396037909576032E-02 2.9865810126131473E-02 3.0341995262508869E-02 3.0824663023315265E-02 3.1313883340324034E-02 3.1809726363040781E-02 3.2312262449441513E-02 3.2821562156924181E-02 3.3337696233516109E-02 3.3860735609352044E-02 3.4390751388559723E-02 3.4927814841520896E-02 3.5471997397618416E-02 3.6023370638539901E-02 3.6582006292164834E-02 3.7147976227150749E-02 3.7721352448266347E-02 3.8302207092597775E-02 3.8890612426636606E-02 3.9486640844418289E-02 4.0090364866776945E-02 4.0701857141792065E-02 4.1321190446614746E-02 4.1948437690643652E-02 4.2583671920353360E-02 4.3226966325722864E-02 4.3878394248533757E-02 4.4538029192581562E-02 4.5205944835970645E-02 4.5882215045700031E-02 4.6566913894580300E-02 4.7260115680751363E-02 4.7961894949946529E-02 4.8672326520616711E-02 4.9391485512189783E-02 5.0119447376622127E-02 5.0856287933413583E-02 5.1602083408363128E-02 5.2356910476200856E-02 5.3120846307402506E-02 5.3893968619333266E-02 5.4676355732114719E-02 5.5468086629203522E-02 5.6269241023263590E-02 5.7079899427304126E-02 5.7900143231609309E-02 5.8730054786515599E-02 5.9569717491509799E-02 6.0419215890864554E-02 6.1278635776110597E-02 6.2148064295711257E-02 6.3027590072217532E-02 6.3917303327266098E-02 6.4817296014740178E-02 6.5727661962448516E-02 6.6648497022657571E-02 6.7579899231856019E-02 6.8521968980116144E-02 6.9474809190365944E-02 7.0438525508014160E-02 7.1413226501268662E-02 7.2399023872471963E-02 7.3396032680964257E-02 7.4404371577688450E-02 7.5424163052023319E-02 7.6455533691197869E-02 7.7498614452587697E-02 7.8553540949398551E-02 7.9620453749903203E-02 8.0699498690746815E-02 8.1790827204591951E-02 8.2894596662378195E-02 8.4010970730623732E-02 8.5140119743912404E-02 8.6282221092996284E-02 8.7437459628637415E-02 8.8606028081455221E-02 8.9788127497989631E-02 9.0983967693159015E-02 9.2193767719123645E-02 9.3417756350849382E-02 9.4656172588164597E-02 9.5909266174527566E-02 9.7177298132337775E-02 9.8460541314639369E-02 9.9759280973157907E-02 1.0107381534230878E-01 1.0240445623895514E-01 1.0375152967745704E-01 1.0511537649954371E-01 1.0649635301847789E-01 1.0789483167668136E-01 1.0931120171637761E-01 1.1074586986193020E-01 1.1219926101320916E-01 1.1367181894871320E-01 1.1516400703709533E-01 1.1667630895584083E-01 1.1820922941536172E-01 1.1976329488686480E-01 1.2133905433202732E-01 1.2293707993239000E-01 1.2455796781622287E-01 1.2620233878027204E-01 1.2787083900383339E-01 1.2956414075199946E-01 1.3128294306520824E-01 1.3302797243142106E-01 1.3479998343746188E-01 1.3659975939546654E-01 1.3842811294040713E-01 1.4028588659404562E-01 1.4217395329064522E-01 1.4409321685951945E-01 1.4604461245876685E-01 1.4802910695476554E-01 1.5004769924147585E-01 1.5210142049289424E-01 1.5419133434255880E-01 1.5631853698267853E-01 1.5848415717588524E-01 1.6068935617182453E-01 1.6293532752071124E-01 1.6522329677529582E-01 1.6755452107281577E-01 1.6993028858768022E-01 1.7235191784513354E-01 1.7482075688637408E-01 1.7733818227418710E-01 1.7990559792828550E-01 1.8252443377850061E-01 1.8519614422341002E-01 1.8792220638114437E-01 1.9070411811787397E-01 1.9354339583880292E-01 1.9644157202486379E-01 1.9940019249721602E-01 2.0242081339001983E-01 2.0550499781084910E-01 2.0865431216637012E-01 2.1187032213001347E-01 2.1515458822762096E-01 2.1850866101628649E-01 2.2193407583245175E-01 2.2543234708591747E-01 2.2900496207866716E-01 2.3265337432985025E-01 2.3637899639213325E-01 2.4018319214856038E-01 2.4406726858394825E-01 2.4803246702922807E-01 2.5207995388182225E-01 2.5621081080915908E-01 2.6042602444536217E-01 2.6472647559349183E-01 2.6911292794664765E-01 2.7358601634110535E-01 2.7814623455296744E-01 2.8279392264736453E-01 2.8752925388469530E-01 2.9235222118370052E-01 2.9726262313521978E-01 3.0226004955453523E-01 3.0734386655543561E-01 3.1251320112542114E-01 3.1776692518056587E-01 3.2310363908027490E-01 3.2852165458680305E-01 3.3401897726102392E-01 3.3959328829499819E-01 3.4524192579032759E-01 3.5096186550050434E-01 3.5674970106339199E-01 3.6260162375664029E-01 3.6851340181438635E-01 3.7448035934831347E-01 3.8049735491956466E-01 3.8655875981234800E-01 3.9265843606322759E-01 3.9878971430442356E-01 4.0494537148423432E-01 4.1111760853260731E-01 4.1729802804590754E-01 4.2347761207109158E-01 4.2964670007624256E-01 4.3579496720127597E-01 4.4191140289003816E-01 4.4798429001194034E-01 4.5400118458902738E-01 4.5994889625113156E-01 4.6581346954943037E-01 4.7158016626539134E-01 4.7723344885902169E-01 4.8275696520693484E-01 4.8813353478683058E-01 4.9334513647081496E-01 4.9837289809536534E-01 5.0319708798033924E-01 5.0779710857358895E-01 5.1215149240097768E-01 5.1623790050407614E-01 5.2003312354936204E-01 5.2351308579321343E-01 5.2665285208659895E-01 5.2942663810171608E-01 5.3180782396046622E-01 5.3376897144099866E-01 5.3528184493451092E-01 5.3631743631956841E-01 5.3684599391614363E-01 5.3683705567646944E-01 5.3625948676511070E-01 5.3508152167663825E-01 5.3327081103639962E-01 5.3079447322805973E-01 5.2761915099095280E-01 5.2371107313012177E-01 5.1903612148122558E-01 5.1355990326937695E-01 5.0724782899252563E-01 5.0006519594228538E-01 4.9197727744311759E-01 4.8294941783836032E-01 4.7294713317289827E-01 4.6193621741180263E-01 4.4988285389052401E-01 4.3675373151949493E-01 4.2251616507974643E-01 4.0713821877620077E-01 3.9058883210913015E-01 3.7283794714574836E-01 3.5385663649262544E-01 3.3361723174404029E-01 3.1209345292815610E-01 2.8926054043870764E-01 2.6509539198284149E-01 2.3957670796146016E-01 2.1268514913540087E-01 1.8440351011960338E-01 1.5471691095993800E-01 1.2361300674065680E-01 9.1082212122853196E-02 5.7117934623799410E-02 2.1716808340276526E-02 -1.5121080346699071E-02 -5.3391981455060508E-02 -9.3088287152827007E-02 -1.3419835337779462E-01 -1.7670633346306863E-01 -2.2059201913789936E-01 -2.6583068513875208E-01 -3.1239293533704021E-01 -3.6024454995104971E-01 -4.0934633460888387E-01 -4.5965397267824232E-01 -5.1111788248278178E-01 -5.6368308092930575E-01 -6.1728905479717333E-01 -6.7186964058118193E-01 -7.2735291339876951E-01 -7.8366108512301691E-01 -8.4071041162022664E-01 -8.9841110877600172E-01 -9.5666727689227993E-01 -1.0153768330230137E+00 -1.0744314508729598E+00 -1.1337165079932274E+00 -1.1931110401505141E+00 -1.2524877029084913E+00 -1.3117127406283693E+00 -1.3706459632637569E+00 -1.4291407314891966E+00 -1.4870439508605924E+00 -1.5441960758596749E+00 -1.6004311248247081E+00 -1.6555767069168390E+00 -1.7094540624168537E+00 -1.7618781177912042E+00 -1.8126575571090200E+00 -1.8615949115330717E+00 -1.9084866687468287E+00 -1.9531234043157648E+00 -1.9952899371131263E+00 -2.0347655110672247E+00 -2.0713240056083735E+00 -2.1047341773076864E+00 -2.1347599353067714E+00 -2.1611606532365686E+00 -2.1836915204149419E+00 -2.2021039351967788E+00 -2.2161459434274340E+00 -2.2255627250214460E+00 -2.2300971317542051E+00 -2.2294902794157747E+00 -2.2234821975339067E+00 -2.2118125399280890E+00 -2.1942213594073712E+00 -2.1704499499712702E+00 -2.1402417599128354E+00 -2.1033433792500613E+00 -2.0595056049246305E+00 -2.0084845871930792E+00 -1.9500430605867001E+00 -1.8839516627240820E+00 -1.8099903441040794E+00 -1.7279498717789394E+00 -1.6376334294886832E+00 -1.5388583164132494E+00 -1.4314577461587206E+00 -1.3152827469242723E+00 -1.1902041629940399E+00 -1.0561147567598570E+00 -9.1293140941041462E-01 -7.6059741722911989E-01 -5.9908487913748254E-01 -4.2839716971669478E-01 -2.4857149044711260E-01 -5.9681490326767068E-02 1.3816005464345621E-01 3.4479851541587053E-01 5.6003465156770005E-01 7.8362183717268463E-01 1.0152632899036087E+00 1.2546093253866488E+00 1.5012546623667968E+00 1.7547358084146558E+00 2.0145285607490866E+00 2.2800456622426672E+00 2.5506346587117532E+00 2.8255760099791600E+00 3.1040815136714883E+00 3.3852931069633265E+00 3.6682821171876401E+00 3.9520490371076922E+00 4.2355239044709396E+00 4.5175673681062101E+00 4.7969725242366472E+00 5.0724676068826753E+00 5.3427196152751790E+00 5.6063389591317332E+00 5.8618851994676140E+00 6.1078739582424966E+00 6.3427850644256933E+00 6.5650719967573590E+00 6.7731726742830292E+00 6.9655216342903001E+00 7.1405636232022998E+00 7.2967686089036476E+00 7.4326482025343674E+00 7.5467734536633708E+00 7.6377939546829818E+00 7.7044581580558482E+00 7.7456347735950120E+00 7.7603350722768365E+00 7.7477358783200341E+00 7.7072029827176491E+00 7.6383146595736431E+00 7.5408849121781492E+00 7.4149860196952124E+00 7.2609698988325286E+00 7.0794877393761233E+00 6.8715073197373293E+00 6.6383273606650057E+00 6.3815882342569292E+00 6.1032783138083353E+00 5.8057352304950500E+00 5.4916412981919978E+00 5.1640123807899210E+00 4.8261795102203671E+00 4.4817626211519874E+00 4.1346358531785459E+00 3.7888839865250090E+00 3.4487497260753126E+00 3.1185717339659620E+00 2.8027135358409914E+00 2.5054836922609205E+00 2.2310479359675948E+00 1.9833343272687449E+00 1.7659328717019955E+00 1.5819914713407091E+00 1.4341105356074650E+00 1.3242390474623473E+00 1.2535753499172650E+00 1.2224763650517407E+00 1.2303793568950174E+00 1.2757406696072224E+00 1.3559960776070148E+00 1.4675474351471527E+00 1.6057801674101757E+00 1.7651157611277273E+00 1.9391027498765290E+00 2.1205487129771372E+00 2.3016944922515585E+00 2.4744301667673589E+00 2.6305503200180778E+00 2.7620438185475007E+00 2.8614107561360451E+00 2.9219964960986466E+00 2.9383299938677978E+00 2.9064509666521006E+00 2.8242081946727673E+00 2.6915095169229764E+00 2.5105031730409810E+00 2.2856702985385335E+00 2.0238098531143840E+00 1.7339002708585860E+00 1.4268268273690532E+00 1.1149701982290672E+00 8.1165989034987840E-01 5.3050596412404738E-01 2.8463334874840351E-01 8.5854498311089933E-02 -5.6172660569338208E-02 -1.3474458754889468E-01 -1.4680537606104543E-01 -9.3465184412594965E-02 1.9723110370202097E-02 1.8278854295179217E-01 3.8171293482497054E-01 5.9917094231249768E-01 8.1563298985499211E-01 1.0107895923095920E+00 1.1652165946628228E+00 1.2621614431590615E+00 1.2892951172950775E+00 1.2402479818707723E+00 1.1157361377741930E+00 9.2409318840042665E-01 6.8105494231387920E-01 4.0870362734980153E-01 1.3356280224918726E-01 -1.1606055679624606E-01 -3.1327378289267815E-01 -4.3600929177641740E-01 -4.7022850402375871E-01 -4.1244644600689701E-01 -2.7111180529294238E-01 -6.6459184049652023E-02 1.7138670048459961E-01 4.0603748499554687E-01 5.9989090667185208E-01 7.1999316010628478E-01 7.4384039687373416E-01 6.6408567317181511E-01 4.9111988920054805E-01 2.5270355834779135E-01 -9.7477327347618367E-03 -2.4801161526785304E-01 -4.1612246712543827E-01 -4.8006702791115419E-01 -4.2607563665168280E-01 -2.6539967007643245E-01 -3.3895159782722020E-02 2.1431101751731810E-01 4.1842626030343139E-01 5.2570645600861743E-01 5.0584747118503270E-01 3.6103951962285008E-01 1.2813813599200852E-01 -1.2893558005868491E-01 -3.3581227758131238E-01 -4.2954182821456394E-01 -3.7948334338438117E-01 -2.0010066312468405E-01 5.0022163865607649E-02 2.8478141310601307E-01 4.1916328319848267E-01 4.0094560611699415E-01 2.3360521410060828E-01 -2.0196771346243678E-02 -2.5908964280911712E-01 -3.8245638933313431E-01 -3.3443966847658796E-01 -1.3311385979199297E-01 1.3129465516680627E-01 3.3322904465904646E-01 3.7082479243894850E-01 2.2018373995254886E-01 -4.4803892029351519E-02 -2.8355320902880304E-01 -3.6142667012788326E-01 -2.2825532702021531E-01 4.3555529419591531E-02 2.9157927671091832E-01 3.5740767320570593E-01 1.9049193275072032E-01 -1.0687746736876946E-01 -3.3458174720154193E-01 -3.2697084234119084E-01 -7.7926282751803605E-02 2.3727564566619591E-01 3.7779058920844122E-01 2.2150489792275899E-01 -1.2180859057158659E-01 -3.7595619461661328E-01 -3.1646412944904573E-01 2.5562541814593331E-02 3.6122782570339385E-01 3.7993892884900071E-01 4.0334748934969668E-02 -3.5716593747937780E-01 -4.2531603043262411E-01 -6.9529245463115799E-02 3.7942859735412515E-01 4.6027657360837204E-01 5.7258192834919799E-02 -4.3322876342564814E-01 -4.7956553864918272E-01 5.3268552291382181E-03 5.1467112623388556E-01 4.6628584074991436E-01 -1.2556715432211066E-01 -6.0481597242332352E-01 -3.9380238357226888E-01 3.0057397018459059E-01 6.6701768141602436E-01 2.3695296033239802E-01 -5.0422625617685846E-01 -6.5096517889020744E-01 9.7560108878515760E-03 6.8077139270264464E-01 5.1124467324736489E-01 -3.1246267531092103E-01 -7.5480110353732965E-01 -2.3649609319007675E-01 5.9239232162339184E-01 6.6355778219633599E-01 -1.2822939034357553E-01 -7.4384014577663304E-01 -3.9711073454911333E-01 4.2270724314049707E-01 1.0950105095881897E+00 -2.0118485627624274E+00 7.9497986733923875E+00 -3.1392647203546918E+01 8.6484269815850311E+01 -1.0301655803123639E+02 -8.7477679709431663E+02 9.6581401195452909E+03 -6.5002308314191941E+04 3.5664366775494773E+05 -1.6741945529901101E+06 6.4801892803116813E+06 -1.6311780921830075E+07 -3.0448614283052120E+07 8.5126295190994596E+08 -8.2538537879431839E+09 6.1950906984752480E+10 -4.0041689735808038E+11 2.2535393853038257E+12 -1.0385017174593926E+13 2.7907104678253406E+13 1.4575940723307450E+14 -3.4605628220738260E+15 </ae_partial_wave> <pseudo_partial_wave state= "Ni4" grid="log1"> -2.8282679475320760E-12 -3.3713538873073287E-05 -6.8000845274766074E-05 -1.0287168409140693E-04 -1.3833598639623369E-04 -1.7440385227766132E-04 -2.1108555371568332E-04 -2.4839153750722188E-04 -2.8633242824125982E-04 -3.2491903132460639E-04 -3.6416233605914992E-04 -4.0407351877147924E-04 -4.4466394599576895E-04 -4.8594517771082029E-04 -5.2792897063219635E-04 -5.7062728156037808E-04 -6.1405227078589568E-04 -6.5821630555240823E-04 -7.0313196357871537E-04 -7.4881203664070388E-04 -7.9526953421424557E-04 -8.4251768718009103E-04 -8.9056995159181123E-04 -9.3944001250784864E-04 -9.8914178788878614E-04 -1.0396894325609342E-03 -1.0910973422473642E-03 -1.1433801576675323E-03 -1.1965527687066704E-03 -1.2506303186561260E-03 -1.3056282085258481E-03 -1.3615621014302706E-03 -1.4184479270488131E-03 -1.4763018861622811E-03 -1.5351404552664790E-03 -1.5949803912643026E-03 -1.6558387362376747E-03 -1.7177328223006978E-03 -1.7806802765353623E-03 -1.8446990260112511E-03 -1.9098073028906571E-03 -1.9760236496205496E-03 -2.0433669242129028E-03 -2.1118563056148538E-03 -2.1815112991702382E-03 -2.2523517421740554E-03 -2.3243978095214240E-03 -2.3976700194526602E-03 -2.4721892393961211E-03 -2.5479766919104278E-03 -2.6250539607277946E-03 -2.7034429969001960E-03 -2.7831661250500832E-03 -2.8642460497274322E-03 -2.9467058618749945E-03 -3.0305690454034686E-03 -3.1158594838785955E-03 -3.2026014673219787E-03 -3.2908196991276095E-03 -3.3805393030960631E-03 -3.4717858305883414E-03 -3.5645852678014346E-03 -3.6589640431676225E-03 -3.7549490348796578E-03 -3.8525675785439513E-03 -3.9518474749639489E-03 -4.0528169980558817E-03 -4.1555049028991669E-03 -4.2599404339237670E-03 -4.3661533332367639E-03 -4.4741738490905814E-03 -4.5840327444952086E-03 -4.6957613059769501E-03 -4.8093913524860799E-03 -4.9249552444560214E-03 -5.0424858930165914E-03 -5.1620167693638939E-03 -5.2835819142896022E-03 -5.4072159478722407E-03 -5.5329540793333078E-03 -5.6608321170609332E-03 -5.7908864788040523E-03 -5.9231542020398388E-03 -6.0576729545174556E-03 -6.1944810449810345E-03 -6.3336174340750265E-03 -6.4751217454348401E-03 -6.6190342769661143E-03 -6.7653960123157343E-03 -6.9142486325377466E-03 -7.0656345279576675E-03 -7.2195968102384258E-03 -7.3761793246513345E-03 -7.5354266625556714E-03 -7.6973841740903721E-03 -7.8620979810813015E-03 -8.0296149901679711E-03 -8.1999829061532217E-03 -8.3732502455798382E-03 -8.5494663505377051E-03 -8.7286814027056261E-03 -8.9109464376316925E-03 -9.0963133592561821E-03 -9.2848349546811749E-03 -9.4765649091910487E-03 -9.6715578215280373E-03 -9.8698692194272696E-03 -1.0071555575415479E-02 -1.0276674322878172E-02 -1.0485283872399493E-02 -1.0697443628379356E-02 -1.0913214005932962E-02 -1.1132656448076896E-02 -1.1355833443207125E-02 -1.1582808542873415E-02 -1.1813646379855585E-02 -1.2048412686546273E-02 -1.2287174313645743E-02 -1.2529999249173680E-02 -1.2776956637803641E-02 -1.3028116800525234E-02 -1.3283551254639873E-02 -1.3543332734095510E-02 -1.3807535210166087E-02 -1.4076233912481660E-02 -1.4349505350414810E-02 -1.4627427334829600E-02 -1.4910079000199014E-02 -1.5197540827096977E-02 -1.5489894665071667E-02 -1.5787223755905841E-02 -1.6089612757271381E-02 -1.6397147766783932E-02 -1.6709916346465164E-02 -1.7028007547618629E-02 -1.7351511936126763E-02 -1.7680521618175817E-02 -1.8015130266415751E-02 -1.8355433146562690E-02 -1.8701527144450981E-02 -1.9053510793542588E-02 -1.9411484302901162E-02 -1.9775549585639044E-02 -2.0145810287844269E-02 -2.0522371817996595E-02 -2.0905341376879355E-02 -2.1294827987996871E-02 -2.1690942528504342E-02 -2.2093797760659922E-02 -2.2503508363806667E-02 -2.2920190966893895E-02 -2.3343964181546186E-02 -2.3774948635689502E-02 -2.4213267007743521E-02 -2.4659044061389350E-02 -2.5112406680922256E-02 -2.5573483907198758E-02 -2.6042406974188293E-02 -2.6519309346138768E-02 -2.7004326755366515E-02 -2.7497597240680505E-02 -2.7999261186451539E-02 -2.8509461362336282E-02 -2.9028342963667596E-02 -2.9556053652521383E-02 -3.0092743599471016E-02 -3.0638565526040492E-02 -3.1193674747867949E-02 -3.1758229218590138E-02 -3.2332389574460350E-02 -3.2916319179711093E-02 -3.3510184172673228E-02 -3.4114153512664142E-02 -3.4728399027657314E-02 -3.5353095462744413E-02 -3.5988420529404458E-02 -3.6634554955590995E-02 -3.7291682536651570E-02 -3.7959990187091334E-02 -3.8639667993195292E-02 -3.9330909266521351E-02 -4.0033910598278877E-02 -4.0748871914605411E-02 -4.1475996532756611E-02 -4.2215491218222330E-02 -4.2967566242783771E-02 -4.3732435443526112E-02 -4.4510316282820747E-02 -4.5301429909291958E-02 -4.6106001219783498E-02 -4.6924258922338924E-02 -4.7756435600211977E-02 -4.8602767776921893E-02 -4.9463495982368683E-02 -5.0338864820024802E-02 -5.1229123035218413E-02 -5.2134523584524015E-02 -5.3055323706277288E-02 -5.3991784992228904E-02 -5.4944173460354961E-02 -5.5912759628839369E-02 -5.6897818591245382E-02 -5.7899630092892285E-02 -5.8918478608454117E-02 -5.9954653420797706E-02 -6.1008448701075448E-02 -6.2080163590091136E-02 -6.3170102280955140E-02 -6.4278574103046354E-02 -6.5405893607296234E-02 -6.6552380652815060E-02 -6.7718360494874091E-02 -6.8904163874262903E-02 -7.0110127108038336E-02 -7.1336592181680952E-02 -7.2583906842677723E-02 -7.3852424695545774E-02 -7.5142505298315621E-02 -7.6454514260489118E-02 -7.7788823342489183E-02 -7.9145810556617513E-02 -8.0525860269536106E-02 -8.1929363306287945E-02 -8.3356717055874413E-02 -8.4808325578401095E-02 -8.6284599713810681E-02 -8.7785957192214478E-02 -8.9312822745839238E-02 -9.0865628222600345E-02 -9.2444812701317422E-02 -9.4050822608582038E-02 -9.5684111837292085E-02 -9.7345141866863841E-02 -9.9034381885130154E-02 -1.0075230891193852E-01 -1.0249940792445482E-01 -1.0427617198418389E-01 -1.0608310236571206E-01 -1.0792070868717858E-01 -1.0978950904248364E-01 -1.1169003013523174E-01 -1.1362280741441935E-01 -1.1558838521186431E-01 -1.1758731688137809E-01 -1.1962016493967928E-01 -1.2168750120904601E-01 -1.2378990696170071E-01 -1.2592797306592146E-01 -1.2810230013387044E-01 -1.3031349867112940E-01 -1.3256218922792593E-01 -1.3484900255203999E-01 -1.3717457974336400E-01 -1.3953957241010539E-01 -1.4194464282659705E-01 -1.4439046409269699E-01 -1.4687772029473892E-01 -1.4940710666800572E-01 -1.5197932976068315E-01 -1.5459510759925266E-01 -1.5725516985527951E-01 -1.5996025801353939E-01 -1.6271112554143286E-01 -1.6550853805962398E-01 -1.6835327351383808E-01 -1.7124612234774356E-01 -1.7418788767684174E-01 -1.7717938546327883E-01 -1.8022144469148960E-01 -1.8331490754457194E-01 -1.8646062958128345E-01 -1.8965947991355078E-01 -1.9291234138436270E-01 -1.9622011074591675E-01 -1.9958369883787511E-01 -2.0300403076557669E-01 -2.0648204607804460E-01 -2.1001869894560984E-01 -2.1361495833696342E-01 -2.1727180819544092E-01 -2.2099024761431965E-01 -2.2477129101090085E-01 -2.2861596829913819E-01 -2.3252532506054252E-01 -2.3650042271309299E-01 -2.4054233867785627E-01 -2.4465216654299834E-01 -2.4883101622485232E-01 -2.5308001412568876E-01 -2.5740030328780661E-01 -2.6179304354353927E-01 -2.6625941166074968E-01 -2.7080060148335516E-01 -2.7541782406640114E-01 -2.8011230780516039E-01 -2.8488529855772365E-01 -2.8973805976048467E-01 -2.9467187253591720E-01 -2.9968803579198094E-01 -3.0478786631246246E-01 -3.0997269883751932E-01 -3.1524388613363324E-01 -3.2060279905216144E-01 -3.2605082657558304E-01 -3.3158937585052978E-01 -3.3721987220659305E-01 -3.4294375915986952E-01 -3.4876249840012813E-01 -3.5467756976041970E-01 -3.6069047116787639E-01 -3.6680271857438462E-01 -3.7301584586571146E-01 -3.7933140474760924E-01 -3.8575096460731806E-01 -3.9227611234878185E-01 -3.9890845219982124E-01 -4.0564960548937845E-01 -4.1250121039283633E-01 -4.1946492164331356E-01 -4.2654241020669054E-01 -4.3373536291800346E-01 -4.4104548207668876E-01 -4.4847448499801618E-01 -4.5602410351789974E-01 -4.6369608344808089E-01 -4.7149218397852716E-01 -4.7941417702368055E-01 -4.8746384650899593E-01 -4.9564298759400005E-01 -5.0395340582786019E-01 -5.1239691623323202E-01 -5.2097534231387810E-01 -5.2969051498129438E-01 -5.3854427139529537E-01 -5.4753845371318499E-01 -5.5667490774183315E-01 -5.6595548148663388E-01 -5.7538202359094814E-01 -5.8495638165924235E-01 -5.9468040045675197E-01 -6.0455591997800873E-01 -6.1458477337617057E-01 -6.2476878474454511E-01 -6.3510976674121289E-01 -6.4560951804707456E-01 -6.5626982064707684E-01 -6.6709243692373354E-01 -6.7807910655139803E-01 -6.8923154317903956E-01 -7.0055143088850502E-01 -7.1204042041450233E-01 -7.2370012511162407E-01 -7.3553211665291207E-01 -7.4753792044343370E-01 -7.5971901073139891E-01 -7.7207680539821999E-01 -7.8461266040782007E-01 -7.9732786389424981E-01 -8.1022362986543806E-01 -8.2330109149947750E-01 -8.3656129400849899E-01 -8.5000518704356043E-01 -8.6363361661244376E-01 -8.7744731648048546E-01 -8.9144689902279550E-01 -9.0563284549425804E-01 -9.2000549568172985E-01 -9.3456503690064008E-01 -9.4931149229601297E-01 -9.6424470840545229E-01 -9.7936434193917421E-01 -9.9466984572945183E-01 -1.0101604537990869E+00 -1.0258351654954916E+00 -1.0416927286339597E+00 -1.0577316215902917E+00 -1.0739500342796742E+00 -1.0903458479549897E+00 -1.1069166137540225E+00 -1.1236595299210734E+00 -1.1405714176244048E+00 -1.1576486952866265E+00 -1.1748873513406921E+00 -1.1922829153195593E+00 -1.2098304271827451E+00 -1.2275244047781086E+00 -1.2453588093320598E+00 -1.2633270088561861E+00 -1.2814217393529330E+00 -1.2996350636975285E+00 -1.3179583280678402E+00 -1.3363821157882745E+00 -1.3548961984482701E+00 -1.3734894841504017E+00 -1.3921499627376599E+00 -1.4108646478442224E+00 -1.4296195156088747E+00 -1.4483994398855016E+00 -1.4671881237806872E+00 -1.4859680273444944E+00 -1.5047202912372941E+00 -1.5234246561928628E+00 -1.5420593780964678E+00 -1.5606011384960272E+00 -1.5790249503652125E+00 -1.5973040589396095E+00 -1.6154098374511185E+00 -1.6333116775918053E+00 -1.6509768745468549E+00 -1.6683705064475098E+00 -1.6854553081090322E+00 -1.7021915389366575E+00 -1.7185368449042058E+00 -1.7344461145365755E+00 -1.7498713288585963E+00 -1.7647614053102236E+00 -1.7790620356715843E+00 -1.7927155180923662E+00 -1.8056605833789197E+00 -1.8178322157603002E+00 -1.8291614684320046E+00 -1.8395752742648235E+00 -1.8489962521664707E+00 -1.8573425096973042E+00 -1.8645274426691807E+00 -1.8704595325998004E+00 -1.8750421430552522E+00 -1.8781733160917924E+00 -1.8797455702061006E+00 -1.8796457014223378E+00 -1.8777545893859546E+00 -1.8739470105995863E+00 -1.8680914612268800E+00 -1.8600499922070579E+00 -1.8496780597672757E+00 -1.8368243947925729E+00 -1.8213308949147311E+00 -1.8030325436125560E+00 -1.7817573610761521E+00 -1.7573263920768407E+00 -1.7295537366010489E+00 -1.6982466295488048E+00 -1.6632055763632949E+00 -1.6242245520428151E+00 -1.5810912715867116E+00 -1.5335875405355188E+00 -1.4814896948755421E+00 -1.4245691401802560E+00 -1.3625930004438416E+00 -1.2953248876129519E+00 -1.2225258033257842E+00 -1.1439551848042668E+00 -1.0593721071954585E+00 -9.6853665489735252E-01 -8.7121147450558933E-01 -7.6716352195064719E-01 -6.5616601612548819E-01 -5.3800061079476535E-01 -4.1245979578669445E-01 -2.7934953735440621E-01 -1.3849216610651158E-01 1.0270481002127629E-02 1.6707366051134634E-01 3.3202606293090092E-01 5.0520589614303135E-01 6.8665671814970186E-01 8.7638303038681120E-01 1.0743456483594751E+00 1.2804568726458789E+00 1.4945754903996489E+00 1.7165016453631095E+00 1.9459716230818058E+00 2.1826526074559722E+00 2.4261374749234204E+00 2.6759397033548753E+00 2.9314884840331183E+00 3.1921241367167257E+00 3.4570939395425415E+00 3.7255484971321047E+00 3.9965387814094235E+00 4.2690139899244706E+00 4.5418203754571840E+00 4.8137012078346659E+00 5.0832980336527012E+00 5.3491534013153856E+00 5.6097152168144362E+00 5.8633428892426851E+00 6.1083154134485671E+00 6.3428415197693475E+00 6.5650719967573590E+00 6.7731726742830292E+00 6.9655216342903001E+00 7.1405636232022998E+00 7.2967686089036476E+00 7.4326482025343674E+00 7.5467734536633708E+00 7.6377939546829818E+00 7.7044581580558482E+00 7.7456347735950120E+00 7.7603350722768365E+00 7.7477358783200341E+00 7.7072029827176491E+00 7.6383146595736431E+00 7.5408849121781492E+00 7.4149860196952124E+00 7.2609698988325286E+00 7.0794877393761233E+00 6.8715073197373293E+00 6.6383273606650057E+00 6.3815882342569292E+00 6.1032783138083353E+00 5.8057352304950500E+00 5.4916412981919978E+00 5.1640123807899210E+00 4.8261795102203671E+00 4.4817626211519874E+00 4.1346358531785459E+00 3.7888839865250090E+00 3.4487497260753126E+00 3.1185717339659620E+00 2.8027135358409914E+00 2.5054836922609205E+00 2.2310479359675948E+00 1.9833343272687449E+00 1.7659328717019955E+00 1.5819914713407091E+00 1.4341105356074650E+00 1.3242390474623473E+00 1.2535753499172650E+00 1.2224763650517407E+00 1.2303793568950174E+00 1.2757406696072224E+00 1.3559960776070148E+00 1.4675474351471527E+00 1.6057801674101757E+00 1.7651157611277273E+00 1.9391027498765290E+00 2.1205487129771372E+00 2.3016944922515585E+00 2.4744301667673589E+00 2.6305503200180778E+00 2.7620438185475007E+00 2.8614107561360451E+00 2.9219964960986466E+00 2.9383299938677978E+00 2.9064509666521006E+00 2.8242081946727673E+00 2.6915095169229764E+00 2.5105031730409810E+00 2.2856702985385335E+00 2.0238098531143840E+00 1.7339002708585860E+00 1.4268268273690532E+00 1.1149701982290672E+00 8.1165989034987840E-01 5.3050596412404738E-01 2.8463334874840351E-01 8.5854498311089933E-02 -5.6172660569338208E-02 -1.3474458754889468E-01 -1.4680537606104543E-01 -9.3465184412594965E-02 1.9723110370202097E-02 1.8278854295179217E-01 3.8171293482497054E-01 5.9917094231249768E-01 8.1563298985499211E-01 1.0107895923095920E+00 1.1652165946628228E+00 1.2621614431590615E+00 1.2892951172950775E+00 1.2402479818707723E+00 1.1157361377741930E+00 9.2409318840042665E-01 6.8105494231387920E-01 4.0870362734980153E-01 1.3356280224918726E-01 -1.1606055679624606E-01 -3.1327378289267815E-01 -4.3600929177641740E-01 -4.7022850402375871E-01 -4.1244644600689701E-01 -2.7111180529294238E-01 -6.6459184049652023E-02 1.7138670048459961E-01 4.0603748499554687E-01 5.9989090667185208E-01 7.1999316010628478E-01 7.4384039687373416E-01 6.6408567317181511E-01 4.9111988920054805E-01 2.5270355834779135E-01 -9.7477327347618367E-03 -2.4801161526785304E-01 -4.1612246712543827E-01 -4.8006702791115419E-01 -4.2607563665168280E-01 -2.6539967007643245E-01 -3.3895159782722020E-02 2.1431101751731810E-01 4.1842626030343139E-01 5.2570645600861743E-01 5.0584747118503270E-01 3.6103951962285008E-01 1.2813813599200852E-01 -1.2893558005868491E-01 -3.3581227758131238E-01 -4.2954182821456394E-01 -3.7948334338438117E-01 -2.0010066312468405E-01 5.0022163865607649E-02 2.8478141310601307E-01 4.1916328319848267E-01 4.0094560611699415E-01 2.3360521410060828E-01 -2.0196771346243678E-02 -2.5908964280911712E-01 -3.8245638933313431E-01 -3.3443966847658796E-01 -1.3311385979199297E-01 1.3129465516680627E-01 3.3322904465904646E-01 3.7082479243894850E-01 2.2018373995254886E-01 -4.4803892029351519E-02 -2.8355320902880304E-01 -3.6142667012788326E-01 -2.2825532702021531E-01 4.3555529419591531E-02 2.9157927671091832E-01 3.5740767320570593E-01 1.9049193275072032E-01 -1.0687746736876946E-01 -3.3458174720154193E-01 -3.2697084234119084E-01 -7.7926282751803605E-02 2.3727564566619591E-01 3.7779058920844122E-01 2.2150489792275899E-01 -1.2180859057158659E-01 -3.7595619461661328E-01 -3.1646412944904573E-01 2.5562541814593331E-02 3.6122782570339385E-01 3.7993892884900071E-01 4.0334748934969668E-02 -3.5716593747937780E-01 -4.2531603043262411E-01 -6.9529245463115799E-02 3.7942859735412515E-01 4.6027657360837204E-01 5.7258192834919799E-02 -4.3322876342564814E-01 -4.7956553864918272E-01 5.3268552291382181E-03 5.1467112623388556E-01 4.6628584074991436E-01 -1.2556715432211066E-01 -6.0481597242332352E-01 -3.9380238357226888E-01 3.0057397018459059E-01 6.6701768141602436E-01 2.3695296033239802E-01 -5.0422625617685846E-01 -6.5096517889020744E-01 9.7560108878515760E-03 6.8077139270264464E-01 5.1124467324736489E-01 -3.1246267531092103E-01 -7.5480110353732965E-01 -2.3649609319007675E-01 5.9239232162339184E-01 6.6355778219633599E-01 -1.2822939034357553E-01 -7.4384014577663304E-01 -3.9711073454911333E-01 4.2270724314049707E-01 1.0950105095881897E+00 -2.0118485627624274E+00 7.9497986733923875E+00 -3.1392647203546918E+01 8.6484269815850311E+01 -1.0301655803123639E+02 -8.7477679709431663E+02 9.6581401195452909E+03 -6.5002308314191941E+04 3.5664366775494773E+05 -1.6741945529901101E+06 6.4801892803116813E+06 -1.6311780921830075E+07 -3.0448614283052120E+07 8.5126295190994596E+08 -8.2538537879431839E+09 6.1950906984752480E+10 -4.0041689735808038E+11 2.2535393853038257E+12 -1.0385017174593926E+13 2.7907104678253406E+13 1.4575940723307450E+14 -3.4605628220738260E+15 </pseudo_partial_wave> <projector_function state= "Ni4" grid="log1"> 1.4111572343598541E-11 -1.2784019757135030E-05 -2.5785616313404542E-05 -3.9008488078747106E-05 -5.2456401402643011E-05 -6.6133176462541938E-05 -8.0042713835560422E-05 -9.4188975541010806E-05 -1.0857599286066067E-04 -1.2320786901745003E-04 -1.3808875321428746E-04 -1.5322290029134823E-04 -1.6861460809224397E-04 -1.8426827062498750E-04 -2.0018833948372275E-04 -2.1637935182571333E-04 -2.3284591518684549E-04 -2.4959272103958804E-04 -2.6662454094248544E-04 -2.8394622294409172E-04 -3.0156270042123979E-04 -3.1947899124851740E-04 -3.3770019589511130E-04 -3.5623150604804948E-04 -3.7507819764246445E-04 -3.9424563907408542E-04 -4.1373929107809939E-04 -4.3356470067690164E-04 -4.5372751747505257E-04 -4.7423348307208858E-04 -4.9508843681065208E-04 -5.1629831831448230E-04 -5.3786916698843942E-04 -5.5980712804969536E-04 -5.8211844933868905E-04 -6.0480948231054685E-04 -6.2788669119652918E-04 -6.5135664855008860E-04 -6.7522603647811503E-04 -6.9950165495744477E-04 -7.2419041606402816E-04 -7.4929935188479185E-04 -7.7483561243992460E-04 -8.0080647056973524E-04 -8.2721932301393528E-04 -8.5408169066524084E-04 -8.8140122419620519E-04 -9.0918570534084331E-04 -9.3744304504145412E-04 -9.6618129103047087E-04 -9.9540862821633912E-04 -1.0251333799394496E-03 -1.0553640112050534E-03 -1.0861091316423921E-03 -1.1173774971054899E-03 -1.1491780121056607E-03 -1.1815197336872449E-03 -1.2144118714560832E-03 -1.2478637933370697E-03 -1.2818850256691354E-03 -1.3164852575220148E-03 -1.3516743422716713E-03 -1.3874623009051249E-03 -1.4238593258155123E-03 -1.4608757822916259E-03 -1.4985222112987424E-03 -1.5368093346055970E-03 -1.5757480555886887E-03 -1.6153494631067872E-03 -1.6556248350421950E-03 -1.6965856405471616E-03 -1.7382435452569873E-03 -1.7806104117089891E-03 -1.8236983055101750E-03 -1.8675194971131970E-03 -1.9120864656124461E-03 -1.9574119024928717E-03 -2.0035087156563092E-03 -2.0503900322967447E-03 -2.0980692027804640E-03 -2.1465598049251328E-03 -2.1958756475976807E-03 -2.2460307744028643E-03 -2.2970394680084326E-03 -2.3489162543093751E-03 -2.4016759059364806E-03 -2.4553334471548224E-03 -2.5099041579864749E-03 -2.5654035781451584E-03 -2.6218475114627958E-03 -2.6792520317583820E-03 -2.7376334849718857E-03 -2.7970084962385096E-03 -2.8573939726437999E-03 -2.9188071098804106E-03 -2.9812653953309610E-03 -3.0447866142042008E-03 -3.1093888547849839E-03 -3.1750905120693416E-03 -3.2419102948044159E-03 -3.3098672296072475E-03 -3.3789806669972571E-03 -3.4492702866717861E-03 -3.5207561028262392E-03 -3.5934584703685396E-03 -3.6673980904098169E-03 -3.7425960162108507E-03 -3.8190736589709456E-03 -3.8968527943987231E-03 -3.9759555683663954E-03 -4.0564045033820058E-03 -4.1382225052778504E-03 -4.2214328692566994E-03 -4.3060592866759400E-03 -4.3921258521565729E-03 -4.4796570696753676E-03 -4.5686778604056436E-03 -4.6592135686315730E-03 -4.7512899707094318E-03 -4.8449332802543467E-03 -4.9401701572424862E-03 -5.0370277147573231E-03 -5.1355335270881928E-03 -5.2357156371760092E-03 -5.3376025650719999E-03 -5.4412233153076292E-03 -5.5466073859061250E-03 -5.6537847761713297E-03 -5.7627859954877828E-03 -5.8736420718970579E-03 -5.9863845608435617E-03 -6.1010455541929487E-03 -6.2176576893661489E-03 -6.3362541582801402E-03 -6.4568687172846997E-03 -6.5795356962101573E-03 -6.7042900084658807E-03 -6.8311671606608275E-03 -6.9602032626911899E-03 -7.0914350381740083E-03 -7.2248998345880401E-03 -7.3606356340175025E-03 -7.4986810637728335E-03 -7.6390754073122312E-03 -7.7818586154669708E-03 -7.9270713175680595E-03 -8.0747548330913927E-03 -8.2249511832648819E-03 -8.3777031028146008E-03 -8.5330540521479196E-03 -8.6910482296980226E-03 -8.8517305840998782E-03 -9.0151468272783100E-03 -9.1813434470234701E-03 -9.3503677200435474E-03 -9.5222677257217198E-03 -9.6970923590207272E-03 -9.8748913448073235E-03 -1.0055715251438446E-02 -1.0239615505382405E-02 -1.0426644405260551E-02 -1.0616855136697823E-02 -1.0810301787509470E-02 -1.1007039362506982E-02 -1.1207123799137499E-02 -1.1410611983043365E-02 -1.1617561764286227E-02 -1.1828031973158527E-02 -1.2042082436960026E-02 -1.2259773996575584E-02 -1.2481168523521933E-02 -1.2706328937280430E-02 -1.2935319222960290E-02 -1.3168204448797674E-02 -1.3405050784671279E-02 -1.3645925520402162E-02 -1.3890897084499008E-02 -1.4140035063124303E-02 -1.4393410219603081E-02 -1.4651094513886352E-02 -1.4913161122659637E-02 -1.5179684459571793E-02 -1.5450740195862950E-02 -1.5726405281342542E-02 -1.6006757965534489E-02 -1.6291877819413676E-02 -1.6581845757352408E-02 -1.6876744059244705E-02 -1.7176656393508134E-02 -1.7481667839624526E-02 -1.7791864911837305E-02 -1.8107335582789881E-02 -1.8428169307565689E-02 -1.8754457048167049E-02 -1.9086291298313612E-02 -1.9423766108714970E-02 -1.9766977112750588E-02 -2.0116021552302459E-02 -2.0470998304151042E-02 -2.0832007906900502E-02 -2.1199152588010309E-02 -2.1572536291495911E-02 -2.1952264705802953E-02 -2.2338445292370165E-02 -2.2731187314254823E-02 -2.3130601865636421E-02 -2.3536801901243052E-02 -2.3949902266646214E-02 -2.4370019728619963E-02 -2.4797273006180072E-02 -2.5231782802072843E-02 -2.5673671834468982E-02 -2.6123064869289073E-02 -2.6580088752959554E-02 -2.7044872445618269E-02 -2.7517547054595408E-02 -2.7998245868633954E-02 -2.8487104392329318E-02 -2.8984260381077952E-02 -2.9489853876622080E-02 -3.0004027242744747E-02 -3.0526925201779520E-02 -3.1058694871278367E-02 -3.1599485801289733E-02 -3.2149450012016696E-02 -3.2708742031983644E-02 -3.3277518936586974E-02 -3.3855940387106501E-02 -3.4444168670219412E-02 -3.5042368737763681E-02 -3.5650708247260646E-02 -3.6269357602502113E-02 -3.6898489994728001E-02 -3.7538281444306133E-02 -3.8188910842603639E-02 -3.8850559994421205E-02 -3.9523413660719618E-02 -4.0207659601765824E-02 -4.0903488620625032E-02 -4.1611094606921521E-02 -4.2330674581176557E-02 -4.3062428739105395E-02 -4.3806560496559295E-02 -4.4563276534451204E-02 -4.5332786844227063E-02 -4.6115304773314394E-02 -4.6911047070961887E-02 -4.7720233934244606E-02 -4.8543089054119186E-02 -4.9379839661733115E-02 -5.0230716574845964E-02 -5.1095954244170141E-02 -5.1975790799939345E-02 -5.2870468098288312E-02 -5.3780231767761283E-02 -5.4705331255539655E-02 -5.5646019873697432E-02 -5.6602554845156326E-02 -5.7575197349461454E-02 -5.8564212568196501E-02 -5.9569869730081153E-02 -6.0592442155634051E-02 -6.1632207301314829E-02 -6.2689446803123161E-02 -6.3764446519532822E-02 -6.4857496573676079E-02 -6.5968891394725601E-02 -6.7098929758412001E-02 -6.8247914826427045E-02 -6.9416154184749890E-02 -7.0603959880774517E-02 -7.1811648459085678E-02 -7.3039540995661650E-02 -7.4287963130612006E-02 -7.5557245099064876E-02 -7.6847721760172419E-02 -7.8159732624106165E-02 -7.9493621876775694E-02 -8.0849738402175020E-02 -8.2228435802144562E-02 -8.3630072413298603E-02 -8.5055011321081314E-02 -8.6503620370437656E-02 -8.7976272173211092E-02 -8.9473344111719949E-02 -9.0995218338443540E-02 -9.2542281771475998E-02 -9.4114926085439574E-02 -9.5713547697623039E-02 -9.7338547748903520E-02 -9.8990332079256060E-02 -1.0066931119735877E-01 -1.0237590024401816E-01 -1.0411051894893419E-01 -1.0587359158044747E-01 -1.0766554688776059E-01 -1.0948681803525331E-01 -1.1133784252827185E-01 -1.1321906212998827E-01 -1.1513092276875043E-01 -1.1707387443525924E-01 -1.1904837106911201E-01 -1.2105487043391511E-01 -1.2309383398043110E-01 -1.2516572669692100E-01 -1.2727101694603071E-01 -1.2941017628737198E-01 -1.3158367928497094E-01 -1.3379200329875632E-01 -1.3603562825909954E-01 -1.3831503642346096E-01 -1.4063071211416442E-01 -1.4298314143615071E-01 -1.4537281197361090E-01 -1.4780021246436167E-01 -1.5026583245059577E-01 -1.5277016190482567E-01 -1.5531369082952032E-01 -1.5789690882906313E-01 -1.6052030465245895E-01 -1.6318436570517966E-01 -1.6588957752848771E-01 -1.6863642324445952E-01 -1.7142538296478774E-01 -1.7425693316149690E-01 -1.7713154599741127E-01 -1.8004968861432316E-01 -1.8301182237649141E-01 -1.8601840206713596E-01 -1.8906987503545949E-01 -1.9216668029150008E-01 -1.9530924754612755E-01 -1.9849799619325773E-01 -2.0173333423128201E-01 -2.0501565712053618E-01 -2.0834534657346132E-01 -2.1172276927400979E-01 -2.1514827552261212E-01 -2.1862219780292511E-01 -2.2214484926631167E-01 -2.2571652212991597E-01 -2.2933748598392503E-01 -2.3300798600345371E-01 -2.3672824106027973E-01 -2.4049844172940382E-01 -2.4431874818525337E-01 -2.4818928798206952E-01 -2.5211015371278583E-01 -2.5608140054051931E-01 -2.6010304359646924E-01 -2.6417505523783930E-01 -2.6829736215909356E-01 -2.7246984234960264E-01 -2.7669232189050746E-01 -2.8096457158330723E-01 -2.8528630340242134E-01 -2.8965716676375447E-01 -2.9407674460093280E-01 -2.9854454924069207E-01 -3.0306001806859756E-01 -3.0762250897600441E-01 -3.1223129557898149E-01 -3.1688556219959702E-01 -3.2158439859983773E-01 -3.2632679445816659E-01 -3.3111163357859047E-01 -3.3593768782194894E-01 -3.4080361074903742E-01 -3.4570793096508862E-01 -3.5064904515516915E-01 -3.5562521080005077E-01 -3.6063453856221922E-01 -3.6567498433193629E-01 -3.7074434092347663E-01 -3.7584022941209294E-01 -3.8096009010275861E-01 -3.8610117312237546E-01 -3.9126052862792293E-01 -3.9643499662401444E-01 -4.0162119638448579E-01 -4.0681551547403771E-01 -4.1201409836760750E-01 -4.1721283466707371E-01 -4.2240734691717036E-01 -4.2759297802506108E-01 -4.3276477829106785E-01 -4.3791749206151326E-01 -4.4304554401854623E-01 -4.4814302512637566E-01 -4.5320367825842328E-01 -4.5822088353572232E-01 -4.6318764341340751E-01 -4.6809656755954449E-01 -4.7293985757876589E-01 -4.7770929164249426E-01 -4.8239620909785103E-01 -4.8699149513888157E-01 -4.9148556563655438E-01 -4.9586835223818815E-01 -5.0012928786268274E-01 -5.0425729273527098E-01 -5.0824076112454419E-01 -5.1206754896546391E-01 -5.1572496257491462E-01 -5.1919974869131802E-01 -5.2247808609691870E-01 -5.2554557911073685E-01 -5.2838725327183655E-01 -5.3098755356658711E-01 -5.3333034559000858E-01 -5.3539892007000800E-01 -5.3717600122431275E-01 -5.3864375946300003E-01 -5.3978382899455157E-01 -5.4057733093993876E-01 -5.4100490260706635E-01 -5.4104673362632916E-01 -5.4068260969649173E-01 -5.3989196473766365E-01 -5.3865394229379082E-01 -5.3694746706960950E-01 -5.3475132752486565E-01 -5.3204427047996061E-01 -5.2880510871010755E-01 -5.2501284251699731E-01 -5.2064679626509491E-01 -5.1568677085103809E-01 -5.1011321303525714E-01 -5.0390740250119193E-01 -4.9705165741461610E-01 -4.8952955912889928E-01 -4.8132619651606157E-01 -4.7242843019263303E-01 -4.6282517664754252E-01 -4.5250771196028194E-01 -4.4146999441512391E-01 -4.2970900486476094E-01 -4.1722510316855987E-01 -4.0402239842083548E-01 -3.9010912998865022E-01 -3.7549805559305688E-01 -3.6020684179040691E-01 -3.4425845124194920E-01 -3.2768152010321044E-01 -3.1051071772659922E-01 -2.9278707966193085E-01 -2.7455830367653733E-01 -2.5587899722165713E-01 -2.3681086347468147E-01 -2.1742281182598394E-01 -1.9779097750297003E-01 -1.7799863399219940E-01 -1.5813598110626995E-01 -1.3829979103276049E-01 -1.1859289460233417E-01 -9.9123490444376960E-02 -8.0004260803436922E-02 -6.1351279732152555E-02 -4.3282702341758857E-02 -2.5917227987685237E-02 -9.3723359228719411E-03 6.2377006910396679E-03 2.0804007213802041E-02 3.4225479689448744E-02 4.6411296114242245E-02 5.7283509699652298E-02 6.6779647934269964E-02 7.4855219696993339E-02 8.1486009063682488E-02 8.6670009575624665E-02 9.0428827931739356E-02 9.2808363376503653E-02 9.3878551458240117E-02 9.3731952460850018E-02 9.2480971188243652E-02 9.0253523020892498E-02 8.7187020116608033E-02 8.3420651887292877E-02 7.9086087614364364E-02 7.4296949561475673E-02 6.9137705858047155E-02 6.3653026638605947E-02 5.7839145044076432E-02 5.1639373333911588E-02 4.4946644357721000E-02 3.7616773550200912E-02 2.9497051826138043E-02 2.0475762279243102E-02 1.0559231969303211E-02 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 </projector_function> <ae_partial_wave state= "Ni5" grid="log1"> -1.4880773847593772E-08 1.2738140629138488E-07 4.0338072069867430E-07 7.9747845358124954E-07 1.3000736223690134E-06 1.9076029777147970E-06 2.6176555171750561E-06 3.4297898783449420E-06 4.3446174419627037E-06 5.3638997451652704E-06 6.4894891223562235E-06 7.7232376329446282E-06 9.0679779510350955E-06 1.0526592580627892E-05 1.2102213840920473E-05 1.3798314033185385E-05 1.5618579476413060E-05 1.7566937504662505E-05 1.9647549558952182E-05 2.1864802874143280E-05 2.4223310051200112E-05 2.6727908418650243E-05 2.9383660763726368E-05 3.2195857312171719E-05 3.5170018602004740E-05 3.8311899184469084E-05 4.1627492050304269E-05 4.5123033701977618E-05 4.8805009812424606E-05 5.2680161422843554E-05 5.6755491642643820E-05 6.1038272823126132E-05 6.5536054183319348E-05 7.0256669871998921E-05 7.5208247454513222E-05 8.0399216816847313E-05 8.5838319482520355E-05 9.1534618340568399E-05 9.7497507785112628E-05 1.0373672426892958E-04 1.1026235727509474E-04 1.1708486071221169E-04 1.2421506474000700E-04 1.3166418803320471E-04 1.3944385049261110E-04 1.4756608641327491E-04 1.5604335812044296E-04 1.6488857008483719E-04 1.7411508352953105E-04 1.8373673154142918E-04 1.9376783470104078E-04 2.0422321724491538E-04 2.1511822377576198E-04 2.2646873653591864E-04 2.3829119326047976E-04 2.5060260562702195E-04 2.6342057831950128E-04 2.7676332872453454E-04 2.9064970727891114E-04 3.0509921848782899E-04 3.2013204263399821E-04 3.3576905819841541E-04 3.5203186501427992E-04 3.6894280817620221E-04 3.8652500272754592E-04 4.0480235914944690E-04 4.2379960967576933E-04 4.4354233545898687E-04 4.6405699461272407E-04 4.8537095115744886E-04 5.0751250489658331E-04 5.3051092225109026E-04 5.5439646808140043E-04 5.7920043852636657E-04 6.0495519488977826E-04 6.3169419860582062E-04 6.5945204731574501E-04 6.8826451208891246E-04 7.1816857582228085E-04 7.4920247285334418E-04 7.8140572982247762E-04 8.1481920782162313E-04 8.4948514586722279E-04 8.8544720573633425E-04 9.2275051820587867E-04 9.6144173073602860E-04 1.0015690566397995E-03 1.0431823257820139E-03 1.0863330368518929E-03 1.1310744112546711E-03 1.1774614486687767E-03 1.2255509843162723E-03 1.2754017479954488E-03 1.3270744249256569E-03 1.3806317184556851E-03 1.4361384146882475E-03 1.4936614490743624E-03 1.5532699750327250E-03 1.6150354346504338E-03 1.6790316315227385E-03 1.7453348057908248E-03 1.8140237114379555E-03 1.8851796959056498E-03 1.9588867820929594E-03 2.0352317528032379E-03 2.1143042377042265E-03 2.1961968028686302E-03 2.2810050429638044E-03 2.3688276761605308E-03 2.4597666418323164E-03 2.5539272011180412E-03 2.6514180404221947E-03 2.7523513779283784E-03 2.8568430732031458E-03 2.9650127399686592E-03 3.0769838621240555E-03 3.1928839130967966E-03 3.3128444786066596E-03 3.4370013829263667E-03 3.5654948187242431E-03 3.6984694805755418E-03 3.8360747022304436E-03 3.9784645977279272E-03 4.1257982064460373E-03 4.2782396421801143E-03 4.4359582463418985E-03 4.5991287453733230E-03 4.7679314124700247E-03 4.9425522337104644E-03 5.1231830786875711E-03 5.3100218757406266E-03 5.5032727918858737E-03 5.7031464175451322E-03 5.9098599561721483E-03 6.1236374188770887E-03 6.3447098241498521E-03 6.5733154027832752E-03 6.8096998080973683E-03 7.0541163315659267E-03 7.3068261239464813E-03 7.5680984220146789E-03 7.8382107810033939E-03 8.1174493128465391E-03 8.4061089303267070E-03 8.7044935972247373E-03 9.0129165845682837E-03 9.3317007330748700E-03 9.6611787218835489E-03 1.0001693343667089E-02 1.0353597786214825E-02 1.0717255920573565E-02 1.1093042595831508E-02 1.1481343940626903E-02 1.1882557671459900E-02 1.2297093407882452E-02 1.2725372994636823E-02 1.3167830830809052E-02 1.3624914206058642E-02 1.4097083643980747E-02 1.4584813252650968E-02 1.5088591082397150E-02 1.5608919490835524E-02 1.6146315515201331E-02 1.6701311251996687E-02 1.7274454243969478E-02 1.7866307874428739E-02 1.8477451768892064E-02 1.9108482204050488E-02 1.9760012524025442E-02 2.0432673563880736E-02 2.1127114080340095E-02 2.1844001189647893E-02 2.2584020812496591E-02 2.3347878125929627E-02 2.4136298022113221E-02 2.4950025573853372E-02 2.5789826506717628E-02 2.6656487677601988E-02 2.7550817559564584E-02 2.8473646732726416E-02 2.9425828381018839E-02 3.0408238794533513E-02 3.1421777877208019E-02 3.2467369659553894E-02 3.3545962816108554E-02 3.4658531187264308E-02 3.5806074305098835E-02 3.6989617922801615E-02 3.8210214547258092E-02 3.9468943974321533E-02 4.0766913826266571E-02 4.2105260090883480E-02 4.3485147661633271E-02 4.4907770878245740E-02 4.6374354067100561E-02 4.7886152080689380E-02 4.9444450835413087E-02 5.1050567846920997E-02 5.2705852762153123E-02 5.4411687887194513E-02 5.6169488710002172E-02 5.7980704417009067E-02 5.9846818402557317E-02 6.1769348770053592E-02 6.3749848823683036E-02 6.5789907549455226E-02 6.7891150084295526E-02 7.0055238171829043E-02 7.2283870603438771E-02 7.4578783643112170E-02 7.6941751434518757E-02 7.9374586388691978E-02 8.1879139550612476E-02 8.4457300942917729E-02 8.7110999884882634E-02 8.9842205284741003E-02 9.2652925903334668E-02 9.5545210586997095E-02 9.8521148467496322E-02 1.0158286912677542E-01 1.0473254272414670E-01 1.0797238008350697E-01 1.1130463273805659E-01 1.1473159292991425E-01 1.1825559356193527E-01 1.2187900809894846E-01 1.2560425041554102E-01 1.2943377458743052E-01 1.3337007462337516E-01 1.3741568413448704E-01 1.4157317593772342E-01 1.4584516159024899E-01 1.5023429085127382E-01 1.5474325106789344E-01 1.5937476648137264E-01 1.6413159745024072E-01 1.6901653958648799E-01 1.7403242280108183E-01 1.7918211025495576E-01 1.8446849721155442E-01 1.8989450978696573E-01 1.9546310359361002E-01 2.0117726227341201E-01 2.0703999591633829E-01 2.1305433936014320E-01 2.1922335036714347E-01 2.2555010767381656E-01 2.3203770890901124E-01 2.3868926837655111E-01 2.4550791469802491E-01 2.5249678831157785E-01 2.5965903882254726E-01 2.6699782220183876E-01 2.7451629782799492E-01 2.8221762536899303E-01 2.9010496149990361E-01 2.9818145645266236E-01 3.0645025039434587E-01 3.1491446963051406E-01 3.2357722263037125E-01 3.3244159587072747E-01 3.4151064949600068E-01 3.5078741279178927E-01 3.6027487946988629E-01 3.6997600276297260E-01 3.7989369032764742E-01 3.9003079895490245E-01 4.0039012908764404E-01 4.1097441914539157E-01 4.2178633965682472E-01 4.3282848720141576E-01 4.4410337816191459E-01 4.5561344228997153E-01 4.6736101608759489E-01 4.7934833600745946E-01 4.9157753147518446E-01 5.0405061773659821E-01 5.1676948853255222E-01 5.2973590860303532E-01 5.4295150602103381E-01 5.5641776435479662E-01 5.7013601465482344E-01 5.8410742725903986E-01 5.9833300340635975E-01 6.1281356664528908E-01 6.2754975402073931E-01 6.4254200701909969E-01 6.5779056224940824E-01 6.7329544183764578E-01 6.8905644351240547E-01 7.0507313036391861E-01 7.2134482026507518E-01 7.3787057495283981E-01 7.5464918878115084E-01 7.7167917717165080E-01 7.8895876480548088E-01 8.0648587361701474E-01 8.2425811066740151E-01 8.4227275599109908E-01 8.6052675052096372E-01 8.7901668420607848E-01 8.9773878444054933E-01 9.1668890492055499E-01 9.3586251504050422E-01 9.5525468992708540E-01 9.7486010119239142E-01 9.9467300846467266E-01 1.0146872517290968E+00 1.0348962444832284E+00 1.0552929676858769E+00 1.0758699644565628E+00 1.0966193354691252E+00 1.1175327349785646E+00 1.1386013674253035E+00 1.1598159845741909E+00 1.1811668831639428E+00 1.2026439030630269E+00 1.2242364259470224E+00 1.2459333745279080E+00 1.2677232123761681E+00 1.2895939443820947E+00 1.3115331179036862E+00 1.3335278246465501E+00 1.3555647033174381E+00 1.3776299430887873E+00 1.3997092879078832E+00 1.4217880416815569E+00 1.4438510743659276E+00 1.4658828289905814E+00 1.4878673296475515E+00 1.5097881904771955E+00 1.5316286256852583E+00 1.5533714606277234E+00 1.5749991440023088E+00 1.5964937611873682E+00 1.6178370487704667E+00 1.6390104103098615E+00 1.6599949333724038E+00 1.6807714078911249E+00 1.7013203458846242E+00 1.7216220025785960E+00 1.7416563989670253E+00 1.7614033458469747E+00 1.7808424693561138E+00 1.7999532380362553E+00 1.8187149914390814E+00 1.8371069702817102E+00 1.8551083481499897E+00 1.8726982647361217E+00 1.8898558605847444E+00 1.9065603133078421E+00 1.9227908752143954E+00 1.9385269122856879E+00 1.9537479444126049E+00 1.9684336867976637E+00 1.9825640924133949E+00 1.9961193954011081E+00 2.0090801552919140E+00 2.0214273019367899E+00 2.0331421810463044E+00 2.0442066002650532E+00 2.0546028757418986E+00 2.0643138792048004E+00 2.0733230856065799E+00 2.0816146214711173E+00 2.0891733141298965E+00 2.0959847420833260E+00 2.1020352867302132E+00 2.1073121856547670E+00 2.1118035875088541E+00 2.1154986082364746E+00 2.1183873879151172E+00 2.1204611468002104E+00 2.1217122382454559E+00 2.1221341950719137E+00 2.1217217647869853E+00 2.1204709280272778E+00 2.1183788940366277E+00 2.1154440672929464E+00 2.1116659809637515E+00 2.1070451959793859E+00 2.1015831692042051E+00 2.0952821001256750E+00 2.0881447719253519E+00 2.0801744085621801E+00 2.0713745729477058E+00 2.0617491304941087E+00 2.0513022955324396E+00 2.0400387648732288E+00 2.0279639252203427E+00 2.0150841042406822E+00 2.0014068250640591E+00 1.9869410250594930E+00 1.9716972114403093E+00 1.9556875434995393E+00 1.9389258472884490E+00 1.9214275785068666E+00 1.9032097522393769E+00 1.8842908558974583E+00 1.8646907571639821E+00 1.8444306140399813E+00 1.8235327903037972E+00 1.8020207770474785E+00 1.7799191193237809E+00 1.7572533460911806E+00 1.7340499013675645E+00 1.7103360746173892E+00 1.6861399287574887E+00 1.6614902246564516E+00 1.6364163415283308E+00 1.6109481931146739E+00 1.5851161399650504E+00 1.5589508984431981E+00 1.5324834473001057E+00 1.5057449327756547E+00 1.4787665732331161E+00 1.4515795643143961E+00 1.4242149855464283E+00 1.3967037092456716E+00 1.3690763124702154E+00 1.3413629926662134E+00 1.3135934875528319E+00 1.2857969996914178E+00 1.2580021260918097E+00 1.2302367931227982E+00 1.2025281969146386E+00 1.1749027493693751E+00 1.1473860298290290E+00 1.1200027423923506E+00 1.0927766788173117E+00 1.0657306868988685E+00 1.0388866441693749E+00 1.0122654367323767E+00 9.8588694300930579E-01 9.5977002215269791E-01 9.3393250685901463E-01 9.0839120029882880E-01 8.8316187687198622E-01 8.5825928649016425E-01 8.3369716208894740E-01 8.0948823007567938E-01 7.8564422342780027E-01 7.6217589716839929E-01 7.3909304596111725E-01 7.1640452358463724E-01 6.9411826406644883E-01 6.7224130427702733E-01 6.5077980780648981E-01 6.2973908996598671E-01 6.0912364377831840E-01 5.8893716682620789E-01 5.6918258885891782E-01 5.4986210005737368E-01 5.3097717985889648E-01 5.1252862624995577E-01 4.9451658543019583E-01 4.7694058174401932E-01 4.5979954776642723E-01 4.4309185441875737E-01 4.2681534097906487E-01 4.1096734484288228E-01 3.9554473088496134E-01 3.8054392027317835E-01 3.6596091859376095E-01 3.5179134316365973E-01 3.3803044943174720E-01 3.2467315640533384E-01 3.1171407108071625E-01 2.9914751190350208E-01 2.8696753133235797E-01 2.7516793762380898E-01 2.6374231599042736E-01 2.5268404930509936E-01 2.4198633852601448E-01 2.3164222299843509E-01 2.2164460075063977E-01 2.1198624884595388E-01 2.0265984378640989E-01 1.9365798189405900E-01 1.8497319953173491E-01 1.7659799297385750E-01 1.6852483770545348E-01 1.6074620691693661E-01 1.5325458897320221E-01 1.4604250366534444E-01 1.3910251709681420E-01 1.3242725510718034E-01 1.2600941518983458E-01 1.1984177690990303E-01 1.1391721087151875E-01 1.0822868631724959E-01 1.0276927746607328E-01 9.7532168710235817E-02 9.2510658796768702E-02 8.7698164118006919E-02 8.3088221228861087E-02 7.8674488698527820E-02 7.4450748392213092E-02 7.0410906265481688E-02 6.6548992740940366E-02 6.2859162724789211E-02 5.9335695309812753E-02 5.5972993201950011E-02 5.2765581899911339E-02 4.9708108651519631E-02 4.6795341206620260E-02 4.4022166384520868E-02 4.1383588473915843E-02 3.8874727484950564E-02 3.6490817276218598E-02 3.4227203583677999E-02 3.2079341983218199E-02 3.0042795823335647E-02 2.8113234168435038E-02 2.6286429796037049E-02 2.4558257292100281E-02 2.2924691287299691E-02 2.1381804873191922E-02 1.9925768231091288E-02 1.8552847497589550E-02 1.7259403880716888E-02 1.6041893029264308E-02 1.4896864646033233E-02 1.3820962324814546E-02 1.2810923580559849E-02 1.1863580033965855E-02 1.0975857705379835E-02 1.0144777368987268E-02 9.3674549166435257E-03 8.6411016813443750E-03 7.9630246729570954E-03 7.3306266831340257E-03 6.7414062219464639E-03 6.1929572553438292E-03 5.6829687197140757E-03 5.2092237972837805E-03 4.7695989435771078E-03 4.3620626654195527E-03 3.9846740548260540E-03 3.6355810903851366E-03 3.3130187232913457E-03 3.0153067698580967E-03 2.7408476360498805E-03 2.4881239022184116E-03 2.2556957977546859E-03 2.0421985957626452E-03 1.8463399571535014E-03 1.6668972518421648E-03 1.5027148821400679E-03 1.3527016301713157E-03 1.2158280474131812E-03 1.0911239005145018E-03 9.7767568360926068E-04 8.7462420362714093E-04 7.8116224177981770E-04 6.9653229159487870E-04 6.2002437165091290E-04 5.5097390955953030E-04 4.8875969272167978E-04 4.3280188090083900E-04 3.8256007562498576E-04 3.3753144176001362E-04 2.9724887719287499E-04 2.6127922733041497E-04 2.2922154197592697E-04 2.0070537301905298E-04 1.7538911220896797E-04 1.5295836903364964E-04 1.3312438937072163E-04 1.1562251609121204E-04 1.0021069317998903E-04 8.6668015187076685E-05 7.4793323950051870E-05 6.4403854541040631E-05 5.5333932307014264E-05 4.7433722705024804E-05 4.0568035401072009E-05 3.4615183818400645E-05 2.9465901003207159E-05 2.5022312336686234E-05 2.1196965274220674E-05 1.7911915945811468E-05 1.5097872115368679E-05 1.2693391677429195E-05 1.0644135573867322E-05 8.9021737444414724E-06 7.4253424865111514E-06 6.1766513927656580E-06 5.1237378621486739E-06 4.2383670383210789E-06 3.4959749212595115E-06 2.8752523196500569E-06 2.3577672628673780E-06 1.9276234694454020E-06 1.5711524717186456E-06 1.2766370212520471E-06 1.0340634442036472E-06 8.3490067727560627E-07 6.7190379083160378E-07 5.3893989359272329E-07 4.3083441068029786E-07 3.4323583140168082E-07 2.7249713298308990E-07 2.1557219952766815E-07 1.6992567008768986E-07 1.3345476434931985E-07 1.0442174769031780E-07 8.1395808128688023E-08 6.3203224960222455E-08 4.8884811887438225E-08 3.7659715539097785E-08 2.8894742989529616E-08 2.2078478872319158E-08 1.6799533732813454E-08 1.2728340280708407E-08 9.6019831893378853E-09 7.2116111289704587E-09 5.3920369759683417E-09 4.0131838254210163E-09 2.9730808158262495E-09 2.1921541499425959E-09 1.6085953905623446E-09 1.1746214639870555E-09 8.5346916544518318E-10 6.1699167818773351E-10 4.4374603473826564E-10 3.1747889758137842E-10 2.2593383590821535E-10 1.5991672592915256E-10 1.1256728609686780E-10 7.8794335634495010E-11 5.4840373413233627E-11 3.7947730740570263E-11 2.6104050435098538E-11 1.7849358939318256E-11 1.2130681234248966E-11 8.1931340765607462E-12 5.4988380988081540E-12 3.6669140072478834E-12 2.4293583104053924E-12 1.5988024935969496E-12 1.0451075376861132E-12 6.7848424670212893E-13 4.3740128330720971E-13 2.7998183611266482E-13 1.7792474295812446E-13 1.1223952411296610E-13 7.0275456772895625E-14 4.3667109380506150E-14 2.6924132873596022E-14 1.6470554047974967E-14 9.9952957717218085E-15 6.0165130254529504E-15 3.5916639768535089E-15 2.1261164693718176E-15 1.2478340433013666E-15 7.2600891563034979E-16 4.1867626788437471E-16 2.3927697491146917E-16 1.3550132375857203E-16 7.6021964418160717E-17 4.2249286270721331E-17 2.3254937444035028E-17 1.2675240230675020E-17 6.8402362133051879E-18 3.6541591593820468E-18 1.9321097300151482E-18 1.0109496201346358E-18 5.2336537097570014E-19 2.6802879894617401E-19 1.3576290384714647E-19 6.8002526403696643E-20 3.3676988748363414E-20 1.6486355199999303E-20 7.9765867645017049E-21 3.8135315736936744E-21 1.8012380730297996E-21 8.4035552645510250E-22 3.8718344659087769E-22 1.7613467342543790E-22 7.9096789087365181E-23 3.5056562783987293E-23 1.5331543530609302E-23 6.6148062497198106E-24 2.8149506071543723E-24 1.1812821171628847E-24 4.8873289835319409E-25 1.9931029376065538E-25 8.0099988661728915E-26 3.1716323027046823E-26 1.2370407285712671E-26 4.7516035208189951E-27 1.7969784724657369E-27 6.6896294255252083E-28 2.4516248849724466E-28 8.8320838367623993E-29 3.1071727375619558E-29 1.0741647757452689E-29 3.6479629798417285E-30 1.2166690389255606E-30 </ae_partial_wave> <pseudo_partial_wave state= "Ni5" grid="log1"> 8.2136952690904712E-15 5.3091390216554607E-11 2.1599516782489251E-10 4.9431878225520594E-10 8.9389345083405393E-10 1.4207823724796314E-09 2.0812892324106666E-09 2.8819670080126686E-09 3.8296270863563089E-09 4.9313487042253890E-09 6.1944887218874655E-09 7.6266917422284409E-09 9.2359005872742420E-09 1.1030367144538054E-08 1.3018663596061885E-08 1.5209694043465403E-08 1.7612706542775337E-08 2.0237305563284430E-08 2.3093464885181408E-08 2.6191540951201876E-08 2.9542286688077778E-08 3.3156865814107133E-08 3.7046867649729647E-08 4.1224322448576416E-08 4.5701717267066067E-08 5.0492012391241809E-08 5.5608658340190986E-08 6.1065613466054480E-08 6.6877362171325238E-08 7.3058933764849034E-08 7.9625921978677993E-08 8.6594505168694413E-08 9.3981467222710200E-08 1.0180421920056643E-07 1.1008082173160381E-07 1.1883000819574806E-07 1.2807120871536027E-07 1.3782457498594076E-07 1.4811100597473758E-07 1.5895217451731960E-07 1.7037055484320471E-07 1.8238945106270760E-07 1.9503302664828263E-07 2.0832633494477764E-07 2.2229535074421052E-07 2.3696700296189481E-07 2.5236920845202412E-07 2.6853090700212520E-07 2.8548209754715652E-07 3.0325387564542830E-07 3.2187847225997764E-07 3.4138929389052946E-07 3.6182096410273636E-07 3.8320936650299080E-07 4.0559168920877325E-07 4.2900647086621153E-07 4.5349364826832142E-07 4.7909460562921971E-07 5.0585222557152195E-07 5.3381094188610050E-07 5.6301679412541041E-07 5.9351748409370653E-07 6.2536243429965588E-07 6.5860284843908683E-07 6.9329177397797864E-07 7.2948416690817371E-07 7.6723695875081949E-07 8.0660912588510570E-07 8.4766176128254938E-07 8.9045814872982222E-07 9.3506383962599818E-07 9.8154673244301787E-07 1.0299771549412611E-06 1.0804279492352502E-06 1.1329745598077765E-06 1.1876951245741610E-06 1.2446705691018004E-06 1.3039847040938188E-06 1.3657243262493553E-06 1.4299793226169062E-06 1.4968427785611341E-06 1.5664110894676963E-06 1.6387840763149494E-06 1.7140651052457793E-06 1.7923612112774242E-06 1.8737832262918745E-06 1.9584459114543603E-06 2.0464680942124679E-06 2.1379728100337195E-06 2.2330874490448478E-06 2.3319439077416008E-06 2.4346787459437468E-06 2.5414333491759089E-06 2.6523540966611263E-06 2.7675925351204071E-06 2.8873055585781893E-06 3.0116555943805465E-06 3.1408107956400070E-06 3.2749452403282570E-06 3.4142391372455915E-06 3.5588790391038266E-06 3.7090580629675258E-06 3.8649761183068049E-06 4.0268401429236855E-06 4.1948643470229790E-06 4.3692704657079253E-06 4.5502880201905448E-06 4.7381545880165076E-06 4.9331160826147205E-06 5.1354270424923909E-06 5.3453509304074340E-06 5.5631604428614027E-06 5.7891378302679550E-06 6.0235752281640768E-06 6.2667749998437756E-06 6.5190500908071919E-06 6.7807243954313556E-06 7.0521331362828774E-06 7.3336232565073067E-06 7.6255538257447097E-06 7.9282964600365675E-06 8.2422357562048991E-06 8.5677697412012963E-06 8.9053103369401637E-06 9.2552838411487613E-06 9.6181314247841212E-06 9.9943096465866557E-06 1.0384290985358939E-05 1.0788564390579137E-05 1.1207635851978778E-05 1.1642028988736661E-05 1.2092285658962868E-05 1.2558966590169654E-05 1.3042652031450594E-05 1.3543942428113214E-05 1.4063459119536747E-05 1.4601845061052288E-05 1.5159765570670751E-05 1.5737909101511439E-05 1.6336988040814300E-05 1.6957739536447990E-05 1.7600926351858303E-05 1.8267337750433073E-05 1.8957790410293232E-05 1.9673129370554769E-05 2.0414229010141232E-05 2.1181994060264482E-05 2.1977360651728357E-05 2.2801297398251043E-05 2.3654806517040928E-05 2.4538924987905066E-05 2.5454725752211180E-05 2.6403318953070980E-05 2.7385853218158136E-05 2.8403516986623086E-05 2.9457539881617300E-05 3.0549194129990066E-05 3.1679796030776011E-05 3.2850707474144954E-05 3.4063337512544906E-05 3.5319143985825919E-05 3.6619635202195513E-05 3.7966371676918798E-05 3.9360967930740647E-05 4.0805094350077548E-05 4.2300479111093238E-05 4.3848910169847277E-05 4.5452237320778424E-05 4.7112374325863070E-05 4.8831301116867681E-05 5.0611066073197871E-05 5.2453788377930756E-05 5.4361660454706269E-05 5.6336950488244315E-05 5.8382005031347041E-05 6.0499251701346389E-05 6.2691201969053312E-05 6.4960454043373552E-05 6.7309695854858098E-05 6.9741708141571866E-05 7.2259367640774581E-05 7.4865650390031513E-05 7.7563635141488979E-05 8.0356506893181822E-05 8.3247560541366644E-05 8.6240204658012963E-05 8.9337965397723272E-05 9.2544490538497572E-05 9.5863553660908475E-05 9.9299058470405356E-05 1.0285504326762926E-04 1.0653568557178052E-04 1.1034530690225662E-04 1.1428837772394838E-04 1.1836952256177063E-04 1.2259352529018602E-04 1.2696533460367689E-04 1.3149006967432361E-04 1.3617302600284794E-04 1.4101968146970338E-04 1.4603570259300448E-04 1.5122695100032820E-04 1.5659949012164232E-04 1.6215959211087264E-04 1.6791374500386115E-04 1.7386866012073470E-04 1.8003127972096827E-04 1.8640878491970285E-04 1.9300860387416808E-04 1.9983842024934783E-04 2.0690618197234106E-04 2.1422011028517237E-04 2.2178870910614503E-04 2.2962077471014826E-04 2.3772540573869505E-04 2.4611201355080093E-04 2.5479033292620399E-04 2.6377043313279008E-04 2.7306272937048357E-04 2.8267799460427389E-04 2.9262737179944919E-04 3.0292238657256011E-04 3.1357496027205366E-04 3.2459742350299692E-04 3.3600253011076552E-04 3.4780347163906406E-04 3.6001389227814157E-04 3.7264790431958513E-04 3.8572010413460219E-04 3.9924558869324417E-04 4.1323997264260251E-04 4.2771940596256626E-04 4.4270059221834915E-04 4.5820080742959310E-04 4.7423791957649781E-04 4.9083040876406788E-04 5.0799738806625236E-04 5.2575862507242858E-04 5.4413456415939102E-04 5.6314634951275494E-04 5.8281584892239580E-04 6.0316567837735908E-04 6.2421922748644013E-04 6.4600068575143630E-04 6.6853506972095118E-04 6.9184825105343629E-04 7.1596698551908101E-04 7.4091894297101401E-04 7.6673273831726280E-04 7.9343796352581862E-04 8.2106522069614381E-04 8.4964615623147222E-04 8.7921349614722216E-04 9.0980108255195780E-04 9.4144391133833632E-04 9.7417817112261035E-04 1.0080412834723462E-03 1.0430719444631832E-03 1.0793101676066044E-03 1.1167973281918750E-03 1.1555762090865393E-03 1.1956910480410447E-03 1.2371875865444075E-03 1.2801131202790073E-03 1.3245165512239829E-03 1.3704484414579451E-03 1.4179610687131397E-03 1.4671084837344698E-03 1.5179465694982075E-03 1.5705331023466030E-03 1.6249278150959651E-03 1.6811924621772693E-03 1.7393908868696790E-03 1.7995890906888977E-03 1.8618553049935711E-03 1.9262600648745436E-03 1.9928762853930805E-03 2.0617793402356735E-03 2.1330471428543957E-03 2.2067602301632707E-03 2.2830018488624168E-03 2.3618580444631464E-03 2.4434177530885388E-03 2.5277728961252250E-03 2.6150184778035530E-03 2.7052526857843117E-03 2.7985769948315285E-03 2.8950962736517768E-03 2.9949188949816466E-03 3.0981568490057675E-03 3.2049258601887431E-03 3.3153455076050738E-03 3.4295393488516465E-03 3.5476350476280612E-03 3.6697645050701869E-03 3.7960639949226691E-03 3.9266743026359361E-03 4.0617408684732745E-03 4.2014139347128785E-03 4.3458486970292956E-03 4.4952054601375517E-03 4.6496497977823164E-03 4.8093527171526405E-03 4.9744908278010541E-03 5.1452465151436543E-03 5.3218081186148167E-03 5.5043701145475682E-03 5.6931333038465533E-03 5.8883050045168677E-03 6.0900992491069068E-03 6.2987369871186092E-03 6.5144462924320943E-03 6.7374625757852550E-03 6.9680288023414817E-03 7.2063957143701429E-03 7.4528220590557867E-03 7.7075748214414080E-03 7.9709294625003712E-03 8.2431701623188955E-03 8.5245900683581424E-03 8.8154915487494451E-03 9.1161864505607919E-03 9.4269963629545796E-03 9.7482528851375212E-03 1.0080297898983017E-02 1.0423483846183098E-02 1.0778174009762782E-02 1.1144742799762453E-02 1.1523576042865573E-02 1.1915071275716933E-02 1.2319638041643382E-02 1.2737698190451771E-02 1.3169686180940030E-02 1.3616049385714145E-02 1.4077248397858342E-02 1.4553757338956461E-02 1.5046064167909058E-02 1.5554670989934738E-02 1.6080094365082176E-02 1.6622865615514508E-02 1.7183531130756855E-02 1.7762652670023520E-02 1.8360807660660006E-02 1.8978589491649586E-02 1.9616607801042404E-02 2.0275488756066131E-02 2.0955875324574158E-02 2.1658427536374193E-02 2.2383822732862539E-02 2.3132755803262232E-02 2.3905939405629441E-02 2.4704104170649159E-02 2.5527998886090239E-02 2.6378390659628048E-02 2.7256065057573931E-02 2.8161826216868757E-02 2.9096496927507903E-02 3.0060918682362756E-02 3.1055951691150083E-02 3.2082474855077196E-02 3.3141385698452423E-02 3.4233600253301931E-02 3.5360052892770534E-02 3.6521696108810509E-02 3.7719500229371795E-02 3.8954453070005335E-02 4.0227559514474973E-02 4.1539841018641603E-02 4.2892335031541162E-02 4.4286094327216391E-02 4.5722186240493311E-02 4.7201691799501899E-02 4.8725704747347769E-02 5.0295330444923285E-02 5.1911684646423435E-02 5.3575892138698636E-02 5.5289085235126538E-02 5.7052402114233465E-02 5.8866984992828525E-02 6.0733978122954120E-02 6.2654525601476260E-02 6.4629768980672631E-02 6.6660844667706776E-02 6.8748881100411413E-02 7.0894995686350076E-02 7.3100291491695307E-02 7.5365853666029520E-02 7.7692745588796547E-02 8.0082004722755368E-02 8.2534638159479562E-02 8.5051617841661376E-02 8.7633875446769968E-02 9.0282296916458796E-02 9.2997716616047207E-02 9.5780911108423294E-02 9.8632592526838064E-02 1.0155340153130400E-01 1.0454389983369866E-01 1.0760456227720278E-01 1.1073576845641975E-01 1.1393779386542681E-01 1.1721080056213599E-01 1.2055482733871374E-01 1.2396977938944530E-01 1.2745541746938541E-01 1.3101134653939153E-01 1.3463700389578817E-01 1.3833164678594365E-01 1.4209433951450418E-01 1.4592394004898876E-01 1.4981908613789882E-01 1.5377818095951939E-01 1.5779937832519689E-01 1.6188056746714341E-01 1.6601935744776283E-01 1.7021306123516056E-01 1.7445867949797159E-01 1.7875288418188748E-01 1.8309200194041905E-01 1.8747199750343166E-01 1.9188845707896107E-01 1.9633657189671669E-01 2.0081112201556647E-01 2.0530646053216611E-01 2.0981649834373864E-01 2.1433468963485067E-01 2.1885401827576798E-01 2.2336698533863988E-01 2.2786559795721298E-01 2.3234135977595652E-01 2.3678526325524851E-01 2.4118778412045130E-01 2.4553887826412107E-01 2.4982798143196169E-01 2.5404401204419791E-01 2.5817537752440445E-01 2.6220998452712757E-01 2.6613525347332667E-01 2.6993813781827997E-01 2.7360514848941436E-01 2.7712238394089322E-01 2.8047556627689230E-01 2.8365008389540697E-01 2.8663104109820187E-01 2.8940331509900880E-01 2.9195162084013854E-01 2.9426058399599631E-01 2.9631482249922458E-01 2.9809903686985390E-01 2.9959810955844429E-01 3.0079721342913818E-01 3.0168192940626209E-01 3.0223837318700647E-01 3.0245333078124814E-01 3.0231440247634611E-01 3.0181015463842686E-01 3.0093027855127114E-01 2.9966575525865624E-01 2.9800902511558985E-01 2.9595416046848577E-01 2.9349703957482542E-01 2.9063551954084821E-01 2.8736960570391173E-01 2.8370161451801856E-01 2.7963632662164772E-01 2.7518112638285752E-01 2.7034612383584172E-01 2.6514425455567264E-01 2.5959135267594879E-01 2.5370619195170002E-01 2.4751048952385554E-01 2.4102886687085570E-01 2.3428876235913193E-01 2.2732028985111313E-01 2.2015603802330103E-01 2.1283080541595956E-01 2.0538126680969088E-01 1.9784556733312256E-01 1.9026284178058009E-01 1.8267265798827928E-01 1.7511438480895927E-01 1.6762648726040139E-01 1.6024575381888972E-01 1.5300646359145201E-01 1.4593950422607774E-01 1.3907145488752551E-01 1.3242365240014692E-01 1.2601126267857951E-01 1.1984238374684801E-01 1.1391721087151875E-01 1.0822868631724959E-01 1.0276927746607328E-01 9.7532168710235817E-02 9.2510658796768702E-02 8.7698164118006919E-02 8.3088221228861087E-02 7.8674488698527820E-02 7.4450748392213092E-02 7.0410906265481688E-02 6.6548992740940366E-02 6.2859162724789211E-02 5.9335695309812753E-02 5.5972993201950011E-02 5.2765581899911339E-02 4.9708108651519631E-02 4.6795341206620260E-02 4.4022166384520868E-02 4.1383588473915843E-02 3.8874727484950564E-02 3.6490817276218598E-02 3.4227203583677999E-02 3.2079341983218199E-02 3.0042795823335647E-02 2.8113234168435038E-02 2.6286429796037049E-02 2.4558257292100281E-02 2.2924691287299691E-02 2.1381804873191922E-02 1.9925768231091288E-02 1.8552847497589550E-02 1.7259403880716888E-02 1.6041893029264308E-02 1.4896864646033233E-02 1.3820962324814546E-02 1.2810923580559849E-02 1.1863580033965855E-02 1.0975857705379835E-02 1.0144777368987268E-02 9.3674549166435257E-03 8.6411016813443750E-03 7.9630246729570954E-03 7.3306266831340257E-03 6.7414062219464639E-03 6.1929572553438292E-03 5.6829687197140757E-03 5.2092237972837805E-03 4.7695989435771078E-03 4.3620626654195527E-03 3.9846740548260540E-03 3.6355810903851366E-03 3.3130187232913457E-03 3.0153067698580967E-03 2.7408476360498805E-03 2.4881239022184116E-03 2.2556957977546859E-03 2.0421985957626452E-03 1.8463399571535014E-03 1.6668972518421648E-03 1.5027148821400679E-03 1.3527016301713157E-03 1.2158280474131812E-03 1.0911239005145018E-03 9.7767568360926068E-04 8.7462420362714093E-04 7.8116224177981770E-04 6.9653229159487870E-04 6.2002437165091290E-04 5.5097390955953030E-04 4.8875969272167978E-04 4.3280188090083900E-04 3.8256007562498576E-04 3.3753144176001362E-04 2.9724887719287499E-04 2.6127922733041497E-04 2.2922154197592697E-04 2.0070537301905298E-04 1.7538911220896797E-04 1.5295836903364964E-04 1.3312438937072163E-04 1.1562251609121204E-04 1.0021069317998903E-04 8.6668015187076685E-05 7.4793323950051870E-05 6.4403854541040631E-05 5.5333932307014264E-05 4.7433722705024804E-05 4.0568035401072009E-05 3.4615183818400645E-05 2.9465901003207159E-05 2.5022312336686234E-05 2.1196965274220674E-05 1.7911915945811468E-05 1.5097872115368679E-05 1.2693391677429195E-05 1.0644135573867322E-05 8.9021737444414724E-06 7.4253424865111514E-06 6.1766513927656580E-06 5.1237378621486739E-06 4.2383670383210789E-06 3.4959749212595115E-06 2.8752523196500569E-06 2.3577672628673780E-06 1.9276234694454020E-06 1.5711524717186456E-06 1.2766370212520471E-06 1.0340634442036472E-06 8.3490067727560627E-07 6.7190379083160378E-07 5.3893989359272329E-07 4.3083441068029786E-07 3.4323583140168082E-07 2.7249713298308990E-07 2.1557219952766815E-07 1.6992567008768986E-07 1.3345476434931985E-07 1.0442174769031780E-07 8.1395808128688023E-08 6.3203224960222455E-08 4.8884811887438225E-08 3.7659715539097785E-08 2.8894742989529616E-08 2.2078478872319158E-08 1.6799533732813454E-08 1.2728340280708407E-08 9.6019831893378853E-09 7.2116111289704587E-09 5.3920369759683417E-09 4.0131838254210163E-09 2.9730808158262495E-09 2.1921541499425959E-09 1.6085953905623446E-09 1.1746214639870555E-09 8.5346916544518318E-10 6.1699167818773351E-10 4.4374603473826564E-10 3.1747889758137842E-10 2.2593383590821535E-10 1.5991672592915256E-10 1.1256728609686780E-10 7.8794335634495010E-11 5.4840373413233627E-11 3.7947730740570263E-11 2.6104050435098538E-11 1.7849358939318256E-11 1.2130681234248966E-11 8.1931340765607462E-12 5.4988380988081540E-12 3.6669140072478834E-12 2.4293583104053924E-12 1.5988024935969496E-12 1.0451075376861132E-12 6.7848424670212893E-13 4.3740128330720971E-13 2.7998183611266482E-13 1.7792474295812446E-13 1.1223952411296610E-13 7.0275456772895625E-14 4.3667109380506150E-14 2.6924132873596022E-14 1.6470554047974967E-14 9.9952957717218085E-15 6.0165130254529504E-15 3.5916639768535089E-15 2.1261164693718176E-15 1.2478340433013666E-15 7.2600891563034979E-16 4.1867626788437471E-16 2.3927697491146917E-16 1.3550132375857203E-16 7.6021964418160717E-17 4.2249286270721331E-17 2.3254937444035028E-17 1.2675240230675020E-17 6.8402362133051879E-18 3.6541591593820468E-18 1.9321097300151482E-18 1.0109496201346358E-18 5.2336537097570014E-19 2.6802879894617401E-19 1.3576290384714647E-19 6.8002526403696643E-20 3.3676988748363414E-20 1.6486355199999303E-20 7.9765867645017049E-21 3.8135315736936744E-21 1.8012380730297996E-21 8.4035552645510250E-22 3.8718344659087769E-22 1.7613467342543790E-22 7.9096789087365181E-23 3.5056562783987293E-23 1.5331543530609302E-23 6.6148062497198106E-24 2.8149506071543723E-24 1.1812821171628847E-24 4.8873289835319409E-25 1.9931029376065538E-25 8.0099988661728915E-26 3.1716323027046823E-26 1.2370407285712671E-26 4.7516035208189951E-27 1.7969784724657369E-27 6.6896294255252083E-28 2.4516248849724466E-28 8.8320838367623993E-29 3.1071727375619558E-29 1.0741647757452689E-29 3.6479629798417285E-30 1.2166690389255606E-30 </pseudo_partial_wave> <projector_function state= "Ni5" grid="log1"> -6.2275876136055483E-16 2.3101785798040865E-10 9.3987002212037914E-10 2.1509519361457737E-09 3.8896458971341286E-09 6.1823204327558906E-09 9.0564156249229158E-09 1.2540445824013907E-08 1.6664047200914992E-08 2.1458022089471375E-08 2.6954386285958417E-08 3.3186401504708991E-08 4.0188635555510481E-08 4.7996987261673090E-08 5.6648758743888139E-08 6.6182699182733711E-08 7.6639046137457192E-08 8.8059591430277525E-08 1.0048774384788976E-07 1.1396855501404076E-07 1.2854881825988376E-07 1.4427711750503505E-07 1.6120387508793903E-07 1.7938143993243771E-07 1.9886414915364803E-07 2.1970839778216127E-07 2.4197271075819970E-07 2.6571782729773915E-07 2.9100677569910278E-07 3.1790495098514640E-07 3.4648020952664568E-07 3.7680294895493254E-07 4.0894619977993666E-07 4.4298572292802382E-07 4.7900010557616383E-07 5.1707086885525010E-07 5.5728255500149647E-07 5.9972285240506825E-07 6.4448270085436069E-07 6.9165640159617261E-07 7.4134174854472502E-07 7.9364015213491591E-07 8.4865675262881847E-07 9.0650056380650459E-07 9.6728461080139302E-07 1.0311260712417894E-06 1.0981464258202890E-06 1.1684715916703022E-06 1.2422321071397730E-06 1.3195632847601560E-06 1.4006053679146455E-06 1.4855037218927220E-06 1.5744090037057464E-06 1.6674773545471379E-06 1.7648705904676014E-06 1.8667564131589940E-06 1.9733085925990095E-06 2.0847072092021952E-06 2.2011388577913522E-06 2.3227968838296957E-06 2.4498816258926061E-06 2.5826006384712350E-06 2.7211689918499592E-06 2.8658094699127149E-06 3.0167529175604815E-06 3.1742384530433347E-06 3.3385138092245047E-06 3.5098356102398146E-06 3.6884696894761600E-06 3.8746914191081871E-06 4.0687860272654501E-06 4.2710489651489930E-06 4.4817862496862750E-06 4.7013148374990292E-06 4.9299630143067446E-06 5.1680707768638952E-06 5.4159902644591636E-06 5.6740861517140054E-06 5.9427361251932679E-06 6.2223313079181777E-06 6.5132767394475777E-06 6.8159918679159042E-06 7.1309110379218343E-06 7.4584840254429142E-06 7.7991765774338434E-06 8.1534709428617745E-06 8.5218664853318683E-06 8.9048802581005752E-06 9.3030476149423528E-06 9.7169228687000537E-06 1.0147079932772586E-05 1.0594113012946927E-05 1.1058637319893033E-05 1.1541289782146609E-05 1.2042729816969046E-05 1.2563640105607550E-05 1.3104727412594886E-05 1.3666723408107523E-05 1.4250385552121231E-05 1.4856497957370077E-05 1.5485872373279085E-05 1.6139349081063324E-05 1.6817797932268875E-05 1.7522119357881329E-05 1.8253245425634794E-05 1.9012140949370990E-05 1.9799804613499812E-05 2.0617270162466037E-05 2.1465607608039341E-05 2.2345924488419270E-05 2.3259367170165564E-05 2.4207122197850106E-05 2.5190417678602443E-05 2.6210524738450887E-05 2.7268758996259215E-05 2.8366482111275563E-05 2.9505103383114450E-05 3.0686081399091613E-05 3.1910925735146537E-05 3.3181198736542285E-05 3.4498517327314071E-05 3.5864554903540707E-05 3.7281043307777101E-05 3.8749774822719417E-05 4.0272604275156616E-05 4.1851451203373217E-05 4.3488302097107246E-05 4.5185212699685578E-05 4.6944310418716017E-05 4.8767796790198175E-05 5.0657950043937224E-05 5.2617127767029169E-05 5.4647769635615893E-05 5.6752400249705044E-05 5.8933632065956147E-05 6.1194168449778605E-05 6.3536806790459225E-05 6.5964441770110220E-05 6.8480068705067645E-05 7.1086787039477932E-05 7.3787803921513632E-05 7.6586437933060816E-05 7.9486122936124338E-05 8.2490412043006815E-05 8.5602981730400530E-05 8.8827636115305580E-05 9.2168311328319979E-05 9.5629080088024769E-05 9.9214156407380255E-05 1.0292790046052014E-04 1.0677482363296023E-04 1.1075959372107419E-04 1.1488704032949576E-04 1.1916216045707176E-04 1.2359012424896786E-04 1.2817628097649408E-04 1.3292616520817077E-04 1.3784550318676628E-04 1.4294021942418722E-04 1.4821644356148472E-04 1.5368051738732106E-04 1.5933900219258649E-04 1.6519868628625477E-04 1.7126659283241486E-04 1.7754998793129495E-04 1.8405638897585059E-04 1.9079357330566266E-04 1.9776958714674576E-04 2.0499275486578151E-04 2.1247168852442451E-04 2.2021529780701351E-04 2.2823280021956762E-04 2.3653373169932928E-04 2.4512795755187691E-04 2.5402568378520143E-04 2.6323746879867207E-04 2.7277423552517812E-04 2.8264728393703834E-04 2.9286830400097685E-04 3.0344938909137144E-04 3.1440304983461077E-04 3.2574222843588871E-04 3.3748031352596883E-04 3.4963115545487471E-04 3.6220908215943632E-04 3.7522891556872356E-04 3.8870598853591517E-04 4.0265616238482606E-04 4.1709584503361755E-04 4.3204200975063438E-04 4.4751221453995384E-04 4.6352462220121681E-04 4.8009802105482345E-04 4.9725184639247118E-04 5.1500620264893987E-04 5.3338188633624451E-04 5.5240040974603667E-04 5.7208402548008044E-04 5.9245575178394714E-04 6.1353939879925921E-04 6.3535959563819648E-04 6.5794181842998545E-04 6.8131241930302947E-04 7.0549865634872303E-04 7.3052872462879331E-04 7.5643178818274651E-04 7.8323801318348947E-04 8.1097860217476151E-04 8.3968582948851483E-04 8.6939307785539096E-04 9.0013487626316709E-04 9.3194693908575708E-04 9.6486620655496301E-04 9.9893088657807775E-04 1.0341804979868395E-03 1.0706559152410884E-03 1.1083994146489165E-03 1.1474547221312322E-03 1.1878670626102293E-03 1.2296832110679581E-03 1.2729515453059189E-03 1.3177221004916269E-03 1.3640466255448577E-03 1.4119786414012294E-03 1.4615735012641303E-03 1.5128884528426091E-03 1.5659827026864230E-03 1.6209174827060268E-03 1.6777561188602637E-03 1.7365641022087487E-03 1.7974091622733614E-03 1.8603613429077682E-03 1.9254930806335217E-03 1.9928792856499533E-03 2.0625974254798530E-03 2.1347276114385971E-03 2.2093526879511474E-03 2.2865583248234803E-03 2.3664331125945819E-03 2.4490686610062853E-03 2.5345597007664007E-03 2.6230041886129716E-03 2.7145034158924533E-03 2.8091621206665918E-03 2.9070886035238823E-03 3.0083948471510799E-03 3.1131966398781174E-03 3.2216137031604261E-03 3.3337698233399725E-03 3.4497929875732178E-03 3.5698155242433944E-03 3.6939742478984544E-03 3.8224106088877532E-03 3.9552708478074504E-03 4.0927061549244480E-03 4.2348728347276583E-03 4.3819324757500529E-03 4.5340521257961871E-03 4.6914044727762779E-03 4.8541680312891525E-03 5.0225273350739622E-03 5.1966731356171726E-03 5.3768026069444565E-03 5.5631195568892605E-03 5.7558346449430569E-03 5.9551656069238568E-03 6.1613374865960146E-03 6.3745828745067458E-03 6.5951421541290828E-03 6.8232637556242589E-03 7.0592044173140439E-03 7.3032294551517224E-03 7.5556130403488858E-03 7.8166384853748296E-03 8.0865985385427316E-03 8.3657956874083322E-03 8.6545424711619249E-03 8.9531618022647037E-03 9.2619872975196783E-03 9.5813636188294311E-03 9.9116468238038113E-03 1.0253204726508544E-02 1.0606417268511983E-02 1.0971676900485547E-02 1.1349388974561820E-02 1.1739972147673160E-02 1.2143858796076453E-02 1.2561495441282836E-02 1.2993343187604636E-02 1.3439878171507618E-02 1.3901592022974217E-02 1.4378992339092050E-02 1.4872603170028685E-02 1.5382965517546221E-02 1.5910637846319721E-02 1.6456196608114655E-02 1.7020236779020762E-02 1.7603372409899950E-02 1.8206237190119771E-02 1.8829485024737296E-02 1.9473790625192087E-02 2.0139850113580091E-02 2.0828381640612466E-02 2.1540126017237298E-02 2.2275847359951084E-02 2.3036333749844110E-02 2.3822397905267759E-02 2.4634877868102589E-02 2.5474637703523959E-02 2.6342568213145023E-02 2.7239587661355671E-02 2.8166642514695629E-02 2.9124708193994250E-02 3.0114789839027514E-02 3.1137923085370889E-02 3.2195174853057590E-02 3.3287644146709622E-02 3.4416462866583120E-02 3.5582796630122114E-02 3.6787845603404999E-02 3.8032845341871249E-02 3.9319067639717861E-02 4.0647821387169464E-02 4.2020453434917511E-02 4.3438349464820232E-02 4.4902934866064857E-02 4.6415675615725675E-02 4.7978079162839839E-02 4.9591695314849825E-02 5.1258117125340640E-02 5.2978981781918261E-02 5.4755971493043697E-02 5.6590814372529816E-02 5.8485285320509360E-02 6.0441206899516244E-02 6.2460450204442873E-02 6.4544935725000807E-02 6.6696634199467031E-02 6.8917567458386425E-02 7.1209809257091791E-02 7.3575486095814949E-02 7.6016778026452111E-02 7.8535919444931088E-02 8.1135199868509991E-02 8.3816964697401006E-02 8.6583615960310598E-02 8.9437613043932745E-02 9.2381473406534131E-02 9.5417773276327167E-02 9.8549148335725992E-02 1.0177829439299800E-01 1.0510796804358206E-01 1.0854098732387291E-01 1.1208023236111937E-01 1.1572864602391493E-01 1.1948923457876080E-01 1.2336506835922932E-01 1.2735928245556716E-01 1.3147507743384498E-01 1.3571572009532468E-01 1.4008454428842618E-01 1.4458495178741826E-01 1.4922041325411092E-01 1.5399446930095734E-01 1.5891073167642397E-01 1.6397288459618076E-01 1.6918468624641880E-01 1.7454997048877249E-01 1.8007264879961382E-01 1.8575671248002754E-01 1.9160623517660164E-01 1.9762537575711489E-01 2.0381838158955159E-01 2.1018959227719336E-01 2.1674344390732889E-01 2.2348447387576573E-01 2.3041732635437509E-01 2.3754675847387738E-01 2.4487764729900727E-01 2.5241499767836401E-01 2.6016395105585532E-01 2.6812979533542897E-01 2.7631797589488349E-01 2.8473410784826070E-01 2.9338398965931550E-01 3.0227361821072846E-01 3.1140920543444994E-01 3.2079719660840694E-01 3.3044429042225154E-01 3.4035746091082697E-01 3.5054398134704129E-01 3.6101145017617814E-01 3.7176781906043654E-01 3.8282142308523698E-01 3.9418101315689297E-01 4.0585579059398508E-01 4.1785544388126383E-01 4.3019018751456950E-01 4.4287080281690694E-01 4.5590868054869432E-01 4.6931586506822431E-01 4.8310509972034976E-01 4.9728987304140310E-01 5.1188446526508213E-01 5.2690399449620828E-01 5.4236446178618902E-01 5.5828279419377469E-01 5.7467688474722112E-01 5.9156562803744928E-01 6.0896894996604423E-01 6.2690782994630312E-01 6.4540431360971817E-01 6.6448151380466836E-01 6.8416359738933019E-01 7.0447575501819015E-01 7.2544415080329050E-01 7.4709584840030330E-01 7.6945870972992692E-01 7.9256126220192313E-01 8.1643252996942328E-01 8.4110182441282599E-01 8.6659848874611811E-01 8.9295159136553026E-01 9.2018956233565186E-01 9.4833976724798474E-01 9.7742801261053192E-01 1.0074779769563953E+00 1.0385105620186681E+00 1.0705431586356866E+00 1.1035888225543564E+00 1.1376553560219440E+00 1.1727442920324835E+00 1.2088497793581345E+00 1.2459573680843272E+00 1.2840426973165187E+00 1.3230700890693508E+00 1.3629910551176416E+00 1.4037427268085476E+00 1.4452462215247133E+00 1.4874049636584918E+00 1.5301029826044970E+00 1.5732032153833451E+00 1.6165458470361742E+00 1.6599467278181612E+00 1.7031959123841904E+00 1.7460563724869715E+00 1.7882629410502289E+00 1.8295215516551997E+00 1.8695088432683455E+00 1.9078722051844836E+00 1.9442303413662489E+00 1.9781744362956997E+00 2.0092700057498480E+00 2.0370595151743616E+00 2.0610658451418522E+00 2.0807966773149076E+00 2.0957498649604878E+00 2.1054198389673129E+00 2.1093050831170586E+00 2.1069166907191459E+00 2.0977879883726946E+00 2.0814851813976780E+00 2.0576189393292856E+00 2.0258567988938152E+00 1.9859362163619909E+00 1.9376780516076610E+00 1.8810002133517396E+00 1.8159311400208293E+00 1.7426227348431329E+00 1.6613623191098574E+00 1.5725831162945521E+00 1.4768727348042108E+00 1.3749790819111849E+00 1.2678131197246174E+00 1.1564478700631158E+00 1.0421130929915468E+00 9.2618510738694215E-01 8.1017129395782439E-01 6.9568892250396319E-01 5.8443807376587997E-01 4.7816857579825828E-01 3.7864103415981654E-01 2.8758218747420117E-01 2.0663494297561075E-01 1.3730351513098699E-01 8.0894080011133518E-02 3.8451253147041120E-02 1.0690504185764544E-02 -2.0736191125730629E-03 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 </projector_function> <ae_partial_wave state= "Ni6" grid="log1"> 1.4451109795892851E-07 -1.3120203171965237E-06 -4.1533442573345573E-06 -8.2062307952117645E-06 -1.3366692491893894E-05 -1.9599984396755848E-05 -2.6893200836063774E-05 -3.5236498837582297E-05 -4.4633632546096825E-05 -5.5104730005441329E-05 -6.6668073886603087E-05 -7.9342488128409709E-05 -9.3157218239145806E-05 -1.0814181711634934E-04 -1.2432845563542532E-04 -1.4175280774226214E-04 -1.6045273927695110E-04 -1.8046859527557198E-04 -2.0184312624103111E-04 -2.2462140247451700E-04 -2.4885080978669717E-04 -2.7458104279121153E-04 -3.0186411237858630E-04 -3.3075436602751000E-04 -3.6130851730706640E-04 -3.9358568388467980E-04 -4.2764743298928816E-04 -4.6355783351334913E-04 -5.0138351414199265E-04 -5.4119372702121497E-04 -5.8306041658564450E-04 -6.2705829325364045E-04 -6.7326491176789851E-04 -7.2176075401733143E-04 -7.7262931622329445E-04 -8.2595720041232302E-04 -8.8183421013010241E-04 -9.4035345037867359E-04 -1.0016114317819933E-03 -1.0657081790046558E-03 -1.1327473434655910E-03 -1.2028363204033528E-03 -1.2760863703626518E-03 -1.3526127451834161E-03 -1.4325348185841317E-03 -1.5159762214407989E-03 -1.6030649818716313E-03 -1.6939336702459025E-03 -1.7887195492430699E-03 -1.8875647290957660E-03 -1.9906163281572971E-03 -2.0980266389412595E-03 -2.2099532997875856E-03 -2.3265594723159600E-03 -2.4480140248341431E-03 -2.5744917218752201E-03 -2.7061734200443158E-03 -2.8432462703618581E-03 -2.9859039272970194E-03 -3.1343467646915667E-03 -3.2887820987810850E-03 -3.4494244185272541E-03 -3.6164956234817722E-03 -3.7902252694094652E-03 -3.9708508219052250E-03 -4.1586179182466531E-03 -4.3537806377316191E-03 -4.5566017807574218E-03 -4.7673531569059615E-03 -4.9863158823070242E-03 -5.2137806865598085E-03 -5.4500482295009277E-03 -5.6954294281154009E-03 -5.9502457938956010E-03 -6.2148297809618298E-03 -6.4895251452668961E-03 -6.7746873152162209E-03 -7.0706837740440610E-03 -7.3778944542959015E-03 -7.6967121447766348E-03 -8.0275429103338850E-03 -8.3708065248558217E-03 -8.7269369178729784E-03 -9.0963826351639770E-03 -9.4796073137755257E-03 -9.8770901718780099E-03 -1.0289326513888719E-02 -1.0716828251306218E-02 -1.1160124439710404E-02 -1.1619761832394644E-02 -1.2096305451108057E-02 -1.2590339174397886E-02 -1.3102466344054214E-02 -1.3633310390171511E-02 -1.4183515475354062E-02 -1.4753747158605229E-02 -1.5344693079452980E-02 -1.5957063662877767E-02 -1.6591592845621613E-02 -1.7249038824470837E-02 -1.7930184827118591E-02 -1.8635839906226862E-02 -1.9366839757321442E-02 -2.0124047561167691E-02 -2.0908354851288499E-02 -2.1720682407300587E-02 -2.2561981174759209E-02 -2.3433233212215923E-02 -2.4335452666208391E-02 -2.5269686774915891E-02 -2.6237016901228524E-02 -2.7238559595992688E-02 -2.8275467692210156E-02 -2.9348931430982262E-02 -3.0460179620005422E-02 -3.1610480825438374E-02 -3.2801144597976097E-02 -3.4033522733979166E-02 -3.5309010572521407E-02 -3.6629048329232722E-02 -3.7995122467826943E-02 -3.9408767110218713E-02 -4.0871565486145081E-02 -4.2385151423221870E-02 -4.3951210878375044E-02 -4.5571483511601139E-02 -4.7247764303020245E-02 -4.8981905214197506E-02 -5.0775816894717579E-02 -5.2631470435007495E-02 -5.4550899166411239E-02 -5.6536200509527082E-02 -5.8589537871827455E-02 -6.0713142595585017E-02 -6.2909315957135920E-02 -6.5180431218513940E-02 -6.7528935732493078E-02 -6.9957353102076916E-02 -7.2468285395475049E-02 -7.5064415417603114E-02 -7.7748509039143834E-02 -8.0523417584198745E-02 -8.3392080277556485E-02 -8.6357526752594921E-02 -8.9422879620823972E-02 -9.2591357104064784E-02 -9.5866275730245254E-02 -9.9251053093777394E-02 -1.0274921068145881E-01 -1.0636437676482402E-01 -1.1010028935984004E-01 -1.1396079925481876E-01 -1.1794987310738292E-01 -1.2207159661128991E-01 -1.2633017773388036E-01 -1.3072995002487392E-01 -1.3527537599719164E-01 -1.3997105058043138E-01 -1.4482170464757241E-01 -1.4983220861541993E-01 -1.5500757611924357E-01 -1.6035296776198971E-01 -1.6587369493837359E-01 -1.7157522373408135E-01 -1.7746317890022004E-01 -1.8354334790306728E-01 -1.8982168504906949E-01 -1.9630431568493606E-01 -2.0299754047256163E-01 -2.0990783973839197E-01 -2.1704187789671844E-01 -2.2440650794625505E-01 -2.3200877603920569E-01 -2.3985592612187656E-01 -2.4795540464573329E-01 -2.5631486534762254E-01 -2.6494217409770865E-01 -2.7384541381347532E-01 -2.8303288943795218E-01 -2.9251313298010301E-01 -3.0229490861510327E-01 -3.1238721784198598E-01 -3.2279930469590234E-01 -3.3354066101197322E-01 -3.4462103173744563E-01 -3.5605042028857703E-01 -3.6783909394837405E-01 -3.7999758930100330E-01 -3.9253671769835674E-01 -4.0546757075392437E-01 -4.1880152585875713E-01 -4.3255025171394146E-01 -4.4672571387361021E-01 -4.6134018029211665E-01 -4.7640622686856937E-01 -4.9193674298149265E-01 -5.0794493700592003E-01 -5.2444434180474764E-01 -5.4144882018569707E-01 -5.5897257031470271E-01 -5.7703013107604184E-01 -5.9563638736894020E-01 -6.1480657532985483E-01 -6.3455628746902037E-01 -6.5490147770926066E-01 -6.7585846631442703E-01 -6.9744394469419102E-01 -7.1967498007125119E-01 -7.4256901999632641E-01 -7.6614389669561878E-01 -7.9041783123468778E-01 -8.1540943748196204E-01 -8.4113772585433155E-01 -8.6762210682651419E-01 -8.9488239418506366E-01 -9.2293880800712025E-01 -9.5181197734312972E-01 -9.8152294258195727E-01 -1.0120931574759480E+00 -1.0435444908026128E+00 -1.0758992276387589E+00 -1.1091800702219683E+00 -1.1434101383734574E+00 -1.1786129694554062E+00 -1.2148125178349793E+00 -1.2520331538262985E+00 -1.2902996620807452E+00 -1.3296372393950326E+00 -1.3700714919055750E+00 -1.4116284316367944E+00 -1.4543344723700622E+00 -1.4982164247991370E+00 -1.5433014909370337E+00 -1.5896172577384495E+00 -1.6371916899009926E+00 -1.6860531218076920E+00 -1.7362302485724501E+00 -1.7877521161493661E+00 -1.8406481104661656E+00 -1.8949479455412508E+00 -1.9506816505433373E+00 -2.0078795557519986E+00 -2.0665722773769764E+00 -2.1267907011936589E+00 -2.1885659649517115E+00 -2.2519294395135967E+00 -2.3169127086794252E+00 -2.3835475476545511E+00 -2.4518659001161587E+00 -2.5218998538352753E+00 -2.5936816148107886E+00 -2.6672434798723530E+00 -2.7426178077096042E+00 -2.8198369882856147E+00 -2.8989334105934472E+00 -2.9799394287155367E+00 -3.0628873261469258E+00 -3.1478092783447535E+00 -3.2347373134681088E+00 -3.3237032712743702E+00 -3.4147387601403985E+00 -3.5078751121796725E+00 -3.6031433364293339E+00 -3.7005740700846648E+00 -3.8001975277622049E+00 -3.9020434487770621E+00 -4.0061410424245354E+00 -4.1125189312612482E+00 -4.2212050923863984E+00 -4.3322267967292429E+00 -4.4456105463547670E+00 -4.5613820098048690E+00 -4.6795659554977487E+00 -4.8001861832123396E+00 -4.9232654536879217E+00 -5.0488254163701107E+00 -5.1768865353332849E+00 -5.3074680134049332E+00 -5.4405877145089434E+00 -5.5762620842315558E+00 -5.7145060685952487E+00 -5.8553330310018383E+00 -5.9987546672767476E+00 -6.1447809187128772E+00 -6.2934198829761208E+00 -6.4446777226987919E+00 -6.5985585715552402E+00 -6.7550644375912414E+00 -6.9141951035704823E+00 -7.0759480241141093E+00 -7.2403182194476861E+00 -7.4072981656383377E+00 -7.5768776813051781E+00 -7.7490438109166195E+00 -7.9237807049447211E+00 -8.1010694973204522E+00 -8.2808881808147863E+00 -8.4632114811452404E+00 -8.6480107307646392E+00 -8.8352537434161444E+00 -9.0249046906270447E+00 -9.2169239813553663E+00 -9.4112681459936454E+00 -9.6078897258681675E+00 -9.8067371692480751E+00 -1.0007754734697972E+01 -1.0210882402375388E+01 -1.0416055793605837E+01 -1.0623206098784189E+01 -1.0832260013383792E+01 -1.1043139681635235E+01 -1.1255762647296022E+01 -1.1470041810887354E+01 -1.1685885392826671E+01 -1.1903196902020058E+01 -1.2121875109667277E+01 -1.2341814028241263E+01 -1.2562902895799382E+01 -1.2785026165942323E+01 -1.3008063503843980E+01 -1.3231889788832184E+01 -1.3456375124011064E+01 -1.3681384853395450E+01 -1.3906779586989559E+01 -1.4132415234198533E+01 -1.4358143045923523E+01 -1.4583809665663381E+01 -1.4809257189932197E+01 -1.5034323238300955E+01 -1.5258841033382053E+01 -1.5482639491093487E+01 -1.5705543321562402E+01 -1.5927373141051826E+01 -1.6147945595317733E+01 -1.6367073494823575E+01 -1.6584565962255031E+01 -1.6800228592787811E+01 -1.7013863627564618E+01 -1.7225270140834649E+01 -1.7434244241197593E+01 -1.7640579287375655E+01 -1.7844066118908525E+01 -1.8044493302128853E+01 -1.8241647391726840E+01 -1.8435313208152021E+01 -1.8625274131027243E+01 -1.8811312408661959E+01 -1.8993209483651729E+01 -1.9170746334434202E+01 -1.9343703832543778E+01 -1.9511863115165355E+01 -1.9675005972438889E+01 -1.9832915248812078E+01 -1.9985375257588380E+01 -2.0132172207677726E+01 -2.0273094641442402E+01 -2.0407933882452120E+01 -2.0536484491939170E+01 -2.0658544732793438E+01 -2.0773917040077272E+01 -2.0882408497287820E+01 -2.0983831317960465E+01 -2.1078003332690901E+01 -2.1164748482236888E+01 -2.1243897317999586E+01 -2.1315287511793546E+01 -2.1378764377258893E+01 -2.1434181405348998E+01 -2.1481400815762449E+01 -2.1520294124628251E+01 -2.1550742725776715E+01 -2.1572638478108388E+01 -2.1585884284563257E+01 -2.1590394638911061E+01 -2.1586096105433825E+01 -2.1572927684730850E+01 -2.1550841008555327E+01 -2.1519800301044114E+01 -2.1479782046990522E+01 -2.1430774323956115E+01 -2.1372775786805644E+01 -2.1305794341004969E+01 -2.1229845601273865E+01 -2.1144951297302871E+01 -2.1051137846185721E+01 -2.0948435345366299E+01 -2.0836877230788300E+01 -2.0716500775199755E+01 -2.0587348466920002E+01 -2.0449470131508182E+01 -2.0302925488375724E+01 -2.0147786734340357E+01 -1.9984140758634329E+01 -1.9812090713615749E+01 -1.9631756840451640E+01 -1.9443276610717167E+01 -1.9246804344771995E+01 -1.9042510495883153E+01 -1.8830580765395322E+01 -1.8611215167722442E+01 -1.8384627116319344E+01 -1.8151042563513752E+01 -1.7910699200467509E+01 -1.7663845707217234E+01 -1.7410741034379114E+01 -1.7151653695481269E+01 -1.6886861050190863E+01 -1.6616648562460128E+01 -1.6341309022639010E+01 -1.6061141727951263E+01 -1.5776451620715861E+01 -1.5487548387876382E+01 -1.5194745528561704E+01 -1.4898359398515169E+01 -1.4598708241391860E+01 -1.4296111217303965E+01 -1.3990887438782083E+01 -1.3683355023698942E+01 -1.3373830173823654E+01 -1.3062626286660386E+01 -1.2750053107160950E+01 -1.2436415924842859E+01 -1.2122014820829776E+01 -1.1807143968376836E+01 -1.1492090989559989E+01 -1.1177136369995930E+01 -1.0862552932719066E+01 -1.0548605371668765E+01 -1.0235549844633475E+01 -9.9236336249535828E+00 -9.6130948108019236E+00 -9.3041620904369680E+00 -8.9970545614587092E+00 -8.6919816017905092E+00 -8.3891427898607773E+00 -8.0887278712660571E+00 -7.7909167690607708E+00 -7.4958796347368875E+00 -7.2037769369269293E+00 -6.9147595848835852E+00 -6.6289690838539741E+00 -6.3465377195725576E+00 -6.0675887692361927E+00 -5.7922367364929670E+00 -5.5205876081654441E+00 -5.2527391306244597E+00 -4.9887811039345040E+00 -4.7287956920824161E+00 -4.4728577477748281E+00 -4.2210351504592856E+00 -3.9733891562725892E+00 -3.7299747588019576E+00 -3.4908410595301658E+00 -3.2560316468113997E+00 -3.0255849822231342E+00 -2.7995347930647871E+00 -2.5779104696937951E+00 -2.3607374663080387E+00 -2.1480377037166343E+00 -1.9398299726062436E+00 -1.7361303358224391E+00 -1.5369525282578940E+00 -1.3423083530773809E+00 -1.1522080732121058E+00 -9.6666079731110299E-01 -7.8567485962181582E-01 -6.0925819355133026E-01 -4.3741869888951390E-01 -2.7016460280587451E-01 -1.0750481471369702E-01 5.0550725112565489E-02 2.0399070370052555E-01 3.5280210148614066E-01 4.9696986832740353E-01 6.3647661229716679E-01 7.7130230504500119E-01 9.0142400833776060E-01 1.0268156270033215E+00 1.1474476938265403E+00 1.2632871919330357E+00 1.3742974198440749E+00 1.4804379037412814E+00 1.5816643606282010E+00 1.6779287151248370E+00 1.7691791716925451E+00 1.8553603432570565E+00 1.9364134365469250E+00 2.0122764940292166E+00 2.0828846921069344E+00 2.1481706952190973E+00 2.2080650656114251E+00 2.2624967287706697E+00 2.3113934947847214E+00 2.3546826361538731E+00 2.3922915227944963E+00 2.4241483151116148E+00 2.4501827160480913E+00 2.4703267829293338E+00 2.4845157997050391E+00 2.4926892098408802E+00 2.4947916096363092E+00 2.4907738011489831E+00 2.4805939032066133E+00 2.4642185182058962E+00 2.4416239515647109E+00 2.4127974798445648E+00 2.3777386627379435E+00 2.3364606933652943E+00 2.2889917806940834E+00 2.2353765574161195E+00 2.1756775063244445E+00 2.1099763981218551E+00 2.0383757336470176E+00 1.9610001836656732E+00 1.8779980195551629E+00 1.7895425282903814E+00 1.6958334049750683E+00 1.5970981155989386E+00 1.4935932215833043E+00 1.3856056558790888E+00 1.2734539377906289E+00 1.1574893102604393E+00 1.0380967791069506E+00 9.1569602862730437E-01 7.9074218228969906E-01 6.6372637102818566E-01 5.3517606515410521E-01 4.0565511941397658E-01 2.7576347446637872E-01 1.4613645239673004E-01 1.7443579139031020E-02 -1.0961313681260033E-01 -2.3430154189121685E-01 -3.5586236353688278E-01 -4.7351299486596049E-01 -5.8645210292373118E-01 -6.9386511765111858E-01 -7.9493064779004563E-01 -8.8882785591020519E-01 -9.7474480757764603E-01 -1.0518877895333185E+00 -1.1194915688539511E+00 -1.1768305397772278E+00 -1.2232306776154473E+00 -1.2580821904286863E+00 -1.2808527293591361E+00 -1.2911009881935442E+00 -1.2884904922183240E+00 -1.2728033460962116E+00 -1.2439536806074527E+00 -1.2020005089249641E+00 -1.1471596749247777E+00 -1.0798145492557767E+00 -1.0005251040519192E+00 -9.1003497503620623E-01 -8.0927610138727468E-01 -6.9937052048275450E-01 -5.8162888819867842E-01 -4.5754529786280052E-01 -3.2878798456595959E-01 -1.9718552891519564E-01 -6.4708218224866249E-02 6.6555713582160142E-02 1.9442916068280641E-01 3.1668061790415747E-01 4.3106399745423163E-01 5.3536357098704268E-01 6.2744362410564070E-01 7.0530218811585643E-01 7.6712796545666051E-01 8.1135929475113100E-01 8.3674371504014244E-01 8.4239639518935983E-01 8.2785540520045031E-01 7.9313153570071282E-01 7.3875013778952703E-01 6.6578227822089442E-01 5.7586240779983511E-01 4.7118974914108541E-01 3.5451074999973020E-01 2.2908024647582201E-01 9.8599460826971269E-02 -3.2870358441315764E-02 -1.6101894773765540E-01 -2.8142186616863979E-01 -3.8969700751636710E-01 -4.8167912296972559E-01 -5.5360704341700528E-01 -6.0231657502014069E-01 -6.2543035368743394E-01 -6.2153440273160065E-01 -5.9032988725224267E-01 -5.3274776235966481E-01 -4.5101384661416299E-01 -3.4865249488497124E-01 -2.3041866053420151E-01 -1.0215085691218066E-01 2.9458571462264955E-02 1.5717438195277303E-01 2.7360294591499495E-01 3.7163575525947601E-01 4.4492995189049028E-01 4.8839664540454575E-01 4.9866134967721387E-01 4.7445609416907902E-01 4.1690056002037312E-01 3.2963086324921242E-01 2.1874016058940884E-01 9.2505653334328433E-02 -3.9108009580737388E-02 -1.6515883537973625E-01 -2.7461727830858812E-01 -3.5737633798519663E-01 -4.0529777406470752E-01 -4.1318945509224436E-01 -3.7959582223109356E-01 -3.0728197213943648E-01 -2.0330528493263944E-01 -7.8599038417706990E-02 5.2959624018553933E-02 1.7596192366904348E-01 2.7525153189646134E-01 3.3789803716712097E-01 3.5511338884860266E-01 3.2382440843547011E-01 2.4761058797784705E-01 1.3675984037709027E-01 7.2908362360126350E-03 -1.2106414445186377E-01 -2.2774117971484775E-01 -2.9472599531038596E-01 -3.0990349290359143E-01 -2.6974504127972743E-01 -1.8070903328625185E-01 -5.8869140392158452E-02 7.2438142242413545E-02 1.8676580655433303E-01 2.5988816378484486E-01 2.7529608965535024E-01 2.2859939059982456E-01 1.2960052157814012E-01 1.1511077115351001E-03 -1.2542958129009685E-01 -2.1770881598264233E-01 -2.5069671619030032E-01 -2.1437802211840842E-01 -1.1785776869128727E-01 1.1668381091739302E-02 1.3562411941304828E-01 2.1519347860527549E-01 2.2390544149644712E-01 1.5758515664140896E-01 3.7736362858886145E-02 -9.3925271660931064E-02 -1.8914029012581204E-01 -2.1097167841238568E-01 -1.4937373558388489E-01 -2.7653168172204236E-02 1.0439186427455258E-01 1.8976040160020941E-01 1.8918195175970912E-01 1.0090022018785913E-01 -3.5095292080019776E-02 -1.5300334155546663E-01 -1.9235468303267800E-01 -1.3028356845075123E-01 2.5600901157144134E-03 1.3409577538855871E-01 1.8842334952090789E-01 1.3058142561796138E-01 -8.0224269457734483E-03 -1.4287144908860833E-01 -1.8599478845171516E-01 -1.0456229264892428E-01 5.0769473545684361E-02 1.7306753209779546E-01 1.7123626653644755E-01 4.0149906354586644E-02 -1.2596213504170373E-01 -1.9719710413436867E-01 -1.0975046737764053E-01 7.3192196480703492E-02 2.0091328719714366E-01 1.5735639458493456E-01 -3.0286154493298047E-02 -1.9951764339646008E-01 -1.8946550685913943E-01 3.8544712851718197E-03 2.0456100017211423E-01 2.1182402760911384E-01 2.7344518203468605E-03 -2.2223157195508342E-01 -2.2568757188865149E-01 1.4028911731293347E-02 2.5364953769886339E-01 2.2636285349296428E-01 -5.8008942970881647E-02 -2.9364077243048903E-01 -2.0350757552856119E-01 1.3038899011003871E-01 </ae_partial_wave> <pseudo_partial_wave state= "Ni6" grid="log1"> -4.1787802600745015E-14 -2.7010669346530583E-10 -1.0988926894541000E-09 -2.5148863351470923E-09 -4.5477544146118815E-09 -7.2283439366055544E-09 -1.0588725402929207E-08 -1.4662237608941102E-08 -1.9483534029621190E-08 -2.5088630846424822E-08 -3.1514956672074388E-08 -3.8801404032412881E-08 -4.6988382666487431E-08 -5.6117874708144240E-08 -6.6233491814605061E-08 -7.7380534309755515E-08 -8.9606052412217284E-08 -1.0295890962069659E-07 -1.1748984833160619E-07 -1.3325155776654585E-07 -1.5029874428990990E-07 -1.6868820419965968E-07 -1.8847889907716593E-07 -2.0973203378499181E-07 -2.3251113720455925E-07 -2.5688214580880826E-07 -2.8291349016824757E-07 -3.1067618449218755E-07 -3.4024391931045892E-07 -3.7169315740456033E-07 -4.0510323310092426E-07 -4.4055645504289277E-07 -4.7813821256200556E-07 -5.1793708577336936E-07 -5.6004495952417805E-07 -6.0455714132890455E-07 -6.5157248342928737E-07 -7.0119350912200971E-07 -7.5352654350187285E-07 -8.0868184877338777E-07 -8.6677376428895896E-07 -9.2792085147729754E-07 -9.9224604383134828E-07 -1.0598768021308193E-06 -1.1309452750804923E-06 -1.2055884655516568E-06 -1.2839484026205591E-06 -1.3661723196043472E-06 -1.4524128383019770E-06 -1.5428281596546322E-06 -1.6375822610476462E-06 -1.7368451004835262E-06 -1.8407928278636174E-06 -1.9496080036241039E-06 -2.0634798249805261E-06 -2.1826043600437003E-06 -2.3071847900790729E-06 -2.4374316601907842E-06 -2.5735631387215138E-06 -2.7158052856691271E-06 -2.8643923304315472E-06 -3.0195669592019525E-06 -3.1815806123475771E-06 -3.3506937921167058E-06 -3.5271763810305263E-06 -3.7113079713285511E-06 -3.9033782058492092E-06 -4.1036871307401966E-06 -4.3125455604068349E-06 -4.5302754551206845E-06 -4.7572103117252362E-06 -4.9936955678904847E-06 -5.2400890203837614E-06 -5.4967612578402923E-06 -5.7640961085334947E-06 -6.0424911036623846E-06 -6.3323579566910833E-06 -6.6341230592939412E-06 -6.9482279944787806E-06 -7.2751300674804285E-06 -7.6153028550371488E-06 -7.9692367736835075E-06 -8.3374396677152295E-06 -8.7204374175038492E-06 -9.1187745688624522E-06 -9.5330149841879170E-06 -9.9637425161299184E-06 -1.0411561704562750E-05 -1.0877098497662764E-05 -1.1361000997921853E-05 -1.1863940233955700E-05 -1.2386610958995422E-05 -1.2929732476981290E-05 -1.3494049497209384E-05 -1.4080333018514090E-05 -1.4689381244003483E-05 -1.5322020527399625E-05 -1.5979106352071630E-05 -1.6661524343887091E-05 -1.7370191319045856E-05 -1.8106056368100348E-05 -1.8870101977407669E-05 -1.9663345189301887E-05 -2.0486838802318853E-05 -2.1341672612851867E-05 -2.2228974699663552E-05 -2.3149912752728601E-05 -2.4105695447932427E-05 -2.5097573869203277E-05 -2.6126842979709268E-05 -2.7194843143808268E-05 -2.8302961701495916E-05 -2.9452634597157506E-05 -3.0645348064491090E-05 -3.1882640369533331E-05 -3.3166103613786056E-05 -3.4497385599509888E-05 -3.5878191759321967E-05 -3.7310287152308977E-05 -3.8795498528941270E-05 -4.0335716467153637E-05 -4.1932897582037997E-05 -4.3589066811678910E-05 -4.5306319781747289E-05 -4.7086825251560260E-05 -4.8932827644404737E-05 -5.0846649665021541E-05 -5.2830695007242791E-05 -5.4887451154881369E-05 -5.7019492279074124E-05 -5.9229482235392770E-05 -6.1520177664149404E-05 -6.3894431197438726E-05 -6.6355194776584981E-05 -6.8905523083781834E-05 -7.1548577091848633E-05 -7.4287627736155525E-05 -7.7126059712913914E-05 -8.0067375408167041E-05 -8.3115198961969939E-05 -8.6273280472394908E-05 -8.9545500344163668E-05 -9.2935873786867870E-05 -9.6448555467908942E-05 -1.0008784432546831E-04 -1.0385818854699390E-04 -1.0776419071888411E-04 -1.1181061315323619E-04 -1.1600238339773632E-04 -1.2034459993496593E-04 -1.2484253807762286E-04 -1.2950165606637044E-04 -1.3432760137726272E-04 -1.3932621724592690E-04 -1.4450354941593124E-04 -1.4986585311902253E-04 -1.5541960029517331E-04 -1.6117148706065853E-04 -1.6712844143265177E-04 -1.7329763131913205E-04 -1.7968647278318053E-04 -1.8630263859106488E-04 -1.9315406705382662E-04 -2.0024897117241244E-04 -2.0759584809674402E-04 -2.1520348890946138E-04 -2.2308098874545252E-04 -2.3123775725865077E-04 -2.3968352944797835E-04 -2.4842837685471375E-04 -2.5748271914398342E-04 -2.6685733608350283E-04 -2.7656337993314518E-04 -2.8661238825937311E-04 -2.9701629718904187E-04 -3.0778745511758621E-04 -3.1893863688709585E-04 -3.3048305845032820E-04 -3.4243439203723186E-04 -3.5480678184113620E-04 -3.6761486024231992E-04 -3.8087376458729864E-04 -3.9459915454275845E-04 -4.0880723004373733E-04 -4.2351474985628839E-04 -4.3873905077556062E-04 -4.5449806748093399E-04 -4.7081035307056904E-04 -4.8769510029849890E-04 -5.0517216353815060E-04 -5.2326208149700807E-04 -5.4198610070794084E-04 -5.6136619982359787E-04 -5.8142511474112805E-04 -6.0218636458543812E-04 -6.2367427858010804E-04 -6.4591402383608104E-04 -6.6893163408925408E-04 -6.9275403941911453E-04 -7.1740909698167531E-04 -7.4292562279102672E-04 -7.6933342458502217E-04 -7.9666333581173213E-04 -8.2494725077458494E-04 -8.5421816097531978E-04 -8.8451019269520140E-04 -9.1585864585629246E-04 -9.4830003420592922E-04 -9.8187212686901937E-04 -1.0166139913142024E-03 -1.0525660377814811E-03 -1.0897700652204500E-03 -1.1282693087899067E-03 -1.1681084889712437E-03 -1.2093338623498152E-03 -1.2519932741201297E-03 -1.2961362123726687E-03 -1.3418138642219144E-03 -1.3890791738371442E-03 -1.4379869024395764E-03 -1.4885936903314275E-03 -1.5409581210246675E-03 -1.5951407875393286E-03 -1.6512043609435746E-03 -1.7092136612099670E-03 -1.7692357304648059E-03 -1.8313399087098246E-03 -1.8955979120980967E-03 -1.9620839138485553E-03 -2.0308746278862064E-03 -2.1020493952979094E-03 -2.1756902736963283E-03 -2.2518821295876572E-03 -2.3307127338416315E-03 -2.4122728603654226E-03 -2.4966563880861677E-03 -2.5839604063500996E-03 -2.6742853238495732E-03 -2.7677349811926228E-03 -2.8644167672333184E-03 -2.9644417392845363E-03 -3.0679247473386741E-03 -3.1749845624254257E-03 -3.2857440092395798E-03 -3.4003301031758945E-03 -3.5188741919119117E-03 -3.6415121016839386E-03 -3.7683842884053032E-03 -3.8996359937807138E-03 -4.0354174065745669E-03 -4.1758838291957269E-03 -4.3211958497658800E-03 -4.4715195198430438E-03 -4.6270265379768213E-03 -4.7878944392766003E-03 -4.9543067911788858E-03 -5.1264533956049008E-03 -5.3045304977047481E-03 -5.4887410013894061E-03 -5.6792946918570999E-03 -5.8764084653259059E-03 -6.0803065661894692E-03 -6.2912208318185439E-03 -6.5093909452359280E-03 -6.7350646958981722E-03 -6.9684982488225694E-03 -7.2099564223037111E-03 -7.4597129744690188E-03 -7.7180508989282397E-03 -7.9852627297773565E-03 -8.2616508562224061E-03 -8.5475278470944858E-03 -8.8432167855318333E-03 -9.1490516141106201E-03 -9.4653774907102490E-03 -9.7925511554046978E-03 -1.0130941308675333E-02 -1.0480929001245500E-02 -1.0842908035841039E-02 -1.1217285381185231E-02 -1.1604481598539863E-02 -1.2004931281107585E-02 -1.2419083506613630E-02 -1.2847402303386964E-02 -1.3290367130263613E-02 -1.3748473370635426E-02 -1.4222232840968933E-02 -1.4712174314118403E-02 -1.5218844057757376E-02 -1.5742806388250367E-02 -1.6284644240284939E-02 -1.6844959752580466E-02 -1.7424374869985111E-02 -1.8023531962267761E-02 -1.8643094459903618E-02 -1.9283747507144379E-02 -1.9946198632653414E-02 -2.0631178437975350E-02 -2.1339441304095375E-02 -2.2071766116328367E-02 -2.2828957007759762E-02 -2.3611844121441274E-02 -2.4421284391520654E-02 -2.5258162343460188E-02 -2.6123390913470605E-02 -2.7017912287254239E-02 -2.7942698758118847E-02 -2.8898753604482158E-02 -2.9887111986747018E-02 -3.0908841863477633E-02 -3.1965044926758585E-02 -3.3056857556559169E-02 -3.4185451793865118E-02 -3.5352036332271866E-02 -3.6557857527658402E-02 -3.7804200425482284E-02 -3.9092389805146371E-02 -4.0423791240794170E-02 -4.1799812177785285E-02 -4.3221903023992640E-02 -4.4691558254938021E-02 -4.6210317531653854E-02 -4.7779766830014177E-02 -4.9401539580124075E-02 -5.1077317814191892E-02 -5.2808833321126812E-02 -5.4597868805912789E-02 -5.6446259051598918E-02 -5.8355892081525675E-02 -6.0328710319160872E-02 -6.2366711742663415E-02 -6.4471951031011415E-02 -6.6646540698234683E-02 -6.8892652211969260E-02 -7.1212517092208175E-02 -7.3608427985755578E-02 -7.6082739711493652E-02 -7.8637870271155194E-02 -8.1276301819838651E-02 -8.4000581590023563E-02 -8.6813322762327422E-02 -8.9717205275698944E-02 -9.2714976569152757E-02 -9.5809452246529495E-02 -9.9003516655099197E-02 -1.0230012336811523E-01 -1.0570229556067909E-01 -1.0921312626746831E-01 -1.1283577851003503E-01 -1.1657348528047604E-01 -1.2042954936732007E-01 -1.2440734300846072E-01 -1.2851030735488975E-01 -1.3274195172784403E-01 -1.3710585265078115E-01 -1.4160565263632136E-01 -1.4624505870695453E-01 -1.5102784062689442E-01 -1.5595782882096620E-01 -1.6103891195485137E-01 -1.6627503414935435E-01 -1.7167019179962636E-01 -1.7722842996845667E-01 -1.8295383832084355E-01 -1.8885054656505476E-01 -1.9492271936330585E-01 -2.0117455067301260E-01 -2.0761025747730014E-01 -2.1423407286111026E-01 -2.2105023838678570E-01 -2.2806299572049932E-01 -2.3527657745824748E-01 -2.4269519709746906E-01 -2.5032303809753975E-01 -2.5816424196955462E-01 -2.6622289533292359E-01 -2.7450301587329995E-01 -2.8300853713339869E-01 -2.9174329206516841E-01 -3.0071099526879835E-01 -3.0991522384090758E-01 -3.1935939675129704E-01 -3.2904675266463396E-01 -3.3898032612053358E-01 -3.4916292198266946E-01 -3.5959708806494589E-01 -3.7028508584017761E-01 -3.8122885913455556E-01 -3.9243000070909162E-01 -4.0388971662765427E-01 -4.1560878830986975E-01 -4.2758753216639039E-01 -4.3982575671375329E-01 -4.5232271706637966E-01 -4.6507706670438298E-01 -4.7808680641770079E-01 -4.9134923032992295E-01 -5.0486086890907700E-01 -5.1861742887770845E-01 -5.3261372994104927E-01 -5.4684363825999394E-01 -5.6129999660524987E-01 -5.7597455114050955E-01 -5.9085787479606133E-01 -6.0593928721017443E-01 -6.2120677123390466E-01 -6.3664688601620678E-01 -6.5224467671043118E-01 -6.6798358087077370E-01 -6.8384533163844319E-01 -6.9980985785232730E-01 -7.1585518125827452E-01 -7.3195731103492723E-01 -7.4809013590287621E-01 -7.6422531413792527E-01 -7.8033216186885723E-01 -7.9637754010577433E-01 -8.1232574101686272E-01 -8.2813837405006774E-01 -8.4377425258149064E-01 -8.5918928186506727E-01 -8.7433634915814473E-01 -8.8916521700537887E-01 -9.0362242077891497E-01 -9.1765117169617705E-01 -9.3119126666787344E-01 -9.4417900646757780E-01 -9.5654712386055196E-01 -9.6822472348258892E-01 -9.7913723541908515E-01 -9.8920638459955412E-01 -9.9835017829189243E-01 -1.0064829141532070E+00 -1.0135152114674346E+00 -1.0193540683729116E+00 -1.0239029480527064E+00 -1.0270618970242293E+00 -1.0287276988185214E+00 -1.0287940664806727E+00 -1.0271518774454733E+00 -1.0236894544421200E+00 -1.0182928961529143E+00 -1.0108464613861046E+00 -1.0012330105158394E+00 -9.8933450788415511E-01 -9.7503258874202170E-01 -9.5820919411943462E-01 -9.3874727674766223E-01 -9.1653158079887442E-01 -8.9144949774790683E-01 -8.6339200008523054E-01 -8.3225465390673381E-01 -7.9793871056158905E-01 -7.6035227654148640E-01 -7.1941155963016656E-01 -6.7504218798987059E-01 -6.2718059733016585E-01 -5.7577547957630049E-01 -5.2078928452181239E-01 -4.6219976381099037E-01 -4.0000154425150597E-01 -3.3420771491228574E-01 -2.6485140972874777E-01 -1.9198736443603118E-01 -1.1569342360989023E-01 -3.6071970452114042E-02 4.6748751236550590E-02 1.3261345663512641E-01 2.2133881786401974E-01 3.1271268006945452E-01 4.0649353798349885E-01 5.0241031750068321E-01 6.0016250842600005E-01 6.9942069542012908E-01 7.9982753410890717E-01 9.0099921812943540E-01 1.0025274803346571E+00 1.1039821672383647E+00 1.2049144198139279E+00 1.3048604857220043E+00 1.4033461777037497E+00 1.4998919800238684E+00 1.5940187893032722E+00 1.6852542577133995E+00 1.7731396852507915E+00 1.8572373836988856E+00 1.9371384080533651E+00 2.0124705219189973E+00 2.0829062321272538E+00 2.1481706952190973E+00 2.2080650656114251E+00 2.2624967287706697E+00 2.3113934947847214E+00 2.3546826361538731E+00 2.3922915227944963E+00 2.4241483151116148E+00 2.4501827160480913E+00 2.4703267829293338E+00 2.4845157997050391E+00 2.4926892098408802E+00 2.4947916096363092E+00 2.4907738011489831E+00 2.4805939032066133E+00 2.4642185182058962E+00 2.4416239515647109E+00 2.4127974798445648E+00 2.3777386627379435E+00 2.3364606933652943E+00 2.2889917806940834E+00 2.2353765574161195E+00 2.1756775063244445E+00 2.1099763981218551E+00 2.0383757336470176E+00 1.9610001836656732E+00 1.8779980195551629E+00 1.7895425282903814E+00 1.6958334049750683E+00 1.5970981155989386E+00 1.4935932215833043E+00 1.3856056558790888E+00 1.2734539377906289E+00 1.1574893102604393E+00 1.0380967791069506E+00 9.1569602862730437E-01 7.9074218228969906E-01 6.6372637102818566E-01 5.3517606515410521E-01 4.0565511941397658E-01 2.7576347446637872E-01 1.4613645239673004E-01 1.7443579139031020E-02 -1.0961313681260033E-01 -2.3430154189121685E-01 -3.5586236353688278E-01 -4.7351299486596049E-01 -5.8645210292373118E-01 -6.9386511765111858E-01 -7.9493064779004563E-01 -8.8882785591020519E-01 -9.7474480757764603E-01 -1.0518877895333185E+00 -1.1194915688539511E+00 -1.1768305397772278E+00 -1.2232306776154473E+00 -1.2580821904286863E+00 -1.2808527293591361E+00 -1.2911009881935442E+00 -1.2884904922183240E+00 -1.2728033460962116E+00 -1.2439536806074527E+00 -1.2020005089249641E+00 -1.1471596749247777E+00 -1.0798145492557767E+00 -1.0005251040519192E+00 -9.1003497503620623E-01 -8.0927610138727468E-01 -6.9937052048275450E-01 -5.8162888819867842E-01 -4.5754529786280052E-01 -3.2878798456595959E-01 -1.9718552891519564E-01 -6.4708218224866249E-02 6.6555713582160142E-02 1.9442916068280641E-01 3.1668061790415747E-01 4.3106399745423163E-01 5.3536357098704268E-01 6.2744362410564070E-01 7.0530218811585643E-01 7.6712796545666051E-01 8.1135929475113100E-01 8.3674371504014244E-01 8.4239639518935983E-01 8.2785540520045031E-01 7.9313153570071282E-01 7.3875013778952703E-01 6.6578227822089442E-01 5.7586240779983511E-01 4.7118974914108541E-01 3.5451074999973020E-01 2.2908024647582201E-01 9.8599460826971269E-02 -3.2870358441315764E-02 -1.6101894773765540E-01 -2.8142186616863979E-01 -3.8969700751636710E-01 -4.8167912296972559E-01 -5.5360704341700528E-01 -6.0231657502014069E-01 -6.2543035368743394E-01 -6.2153440273160065E-01 -5.9032988725224267E-01 -5.3274776235966481E-01 -4.5101384661416299E-01 -3.4865249488497124E-01 -2.3041866053420151E-01 -1.0215085691218066E-01 2.9458571462264955E-02 1.5717438195277303E-01 2.7360294591499495E-01 3.7163575525947601E-01 4.4492995189049028E-01 4.8839664540454575E-01 4.9866134967721387E-01 4.7445609416907902E-01 4.1690056002037312E-01 3.2963086324921242E-01 2.1874016058940884E-01 9.2505653334328433E-02 -3.9108009580737388E-02 -1.6515883537973625E-01 -2.7461727830858812E-01 -3.5737633798519663E-01 -4.0529777406470752E-01 -4.1318945509224436E-01 -3.7959582223109356E-01 -3.0728197213943648E-01 -2.0330528493263944E-01 -7.8599038417706990E-02 5.2959624018553933E-02 1.7596192366904348E-01 2.7525153189646134E-01 3.3789803716712097E-01 3.5511338884860266E-01 3.2382440843547011E-01 2.4761058797784705E-01 1.3675984037709027E-01 7.2908362360126350E-03 -1.2106414445186377E-01 -2.2774117971484775E-01 -2.9472599531038596E-01 -3.0990349290359143E-01 -2.6974504127972743E-01 -1.8070903328625185E-01 -5.8869140392158452E-02 7.2438142242413545E-02 1.8676580655433303E-01 2.5988816378484486E-01 2.7529608965535024E-01 2.2859939059982456E-01 1.2960052157814012E-01 1.1511077115351001E-03 -1.2542958129009685E-01 -2.1770881598264233E-01 -2.5069671619030032E-01 -2.1437802211840842E-01 -1.1785776869128727E-01 1.1668381091739302E-02 1.3562411941304828E-01 2.1519347860527549E-01 2.2390544149644712E-01 1.5758515664140896E-01 3.7736362858886145E-02 -9.3925271660931064E-02 -1.8914029012581204E-01 -2.1097167841238568E-01 -1.4937373558388489E-01 -2.7653168172204236E-02 1.0439186427455258E-01 1.8976040160020941E-01 1.8918195175970912E-01 1.0090022018785913E-01 -3.5095292080019776E-02 -1.5300334155546663E-01 -1.9235468303267800E-01 -1.3028356845075123E-01 2.5600901157144134E-03 1.3409577538855871E-01 1.8842334952090789E-01 1.3058142561796138E-01 -8.0224269457734483E-03 -1.4287144908860833E-01 -1.8599478845171516E-01 -1.0456229264892428E-01 5.0769473545684361E-02 1.7306753209779546E-01 1.7123626653644755E-01 4.0149906354586644E-02 -1.2596213504170373E-01 -1.9719710413436867E-01 -1.0975046737764053E-01 7.3192196480703492E-02 2.0091328719714366E-01 1.5735639458493456E-01 -3.0286154493298047E-02 -1.9951764339646008E-01 -1.8946550685913943E-01 3.8544712851718197E-03 2.0456100017211423E-01 2.1182402760911384E-01 2.7344518203468605E-03 -2.2223157195508342E-01 -2.2568757188865149E-01 1.4028911731293347E-02 2.5364953769886339E-01 2.2636285349296428E-01 -5.8008942970881647E-02 -2.9364077243048903E-01 -2.0350757552856119E-01 1.3038899011003871E-01 </pseudo_partial_wave> <projector_function state= "Ni6" grid="log1"> -3.5940197368644425E-13 -3.3462954937959125E-10 -1.3613396598834537E-09 -3.1155255322547744E-09 -5.6338646789601971E-09 -8.9546763261635036E-09 -1.3117626557047492E-08 -1.8163998619291625E-08 -2.4136744393397128E-08 -3.1080504071367118E-08 -3.9041615123540920E-08 -4.8068283226966460E-08 -5.8210514284548180E-08 -6.9520389705802033E-08 -8.2051911918570644E-08 -9.5861175773363316E-08 -1.1100650602866112E-07 -1.2754842331475773E-07 -1.4554972706928377E-07 -1.6507579425795248E-07 -1.8619436533375203E-07 -2.0897573504381831E-07 -2.3349302711947839E-07 -2.5982202765333049E-07 -2.8804144862208777E-07 -3.1823296695522671E-07 -3.5048136374361141E-07 -3.8487462555019515E-07 -4.2150401811084525E-07 -4.6046428527843626E-07 -5.0185369938946541E-07 -5.4577420857195483E-07 -5.9233163045382182E-07 -6.4163570028393385E-07 -6.9380025803832709E-07 -7.4894332147261480E-07 -8.0718741532839738E-07 -8.6865950799524053E-07 -9.3349132834724606E-07 -1.0018195100152808E-06 -1.0737856993771532E-06 -1.1495367209650079E-06 -1.2292248955228823E-06 -1.3130081536713534E-06 -1.4010501946122593E-06 -1.4935207565877270E-06 -1.5905957477644735E-06 -1.6924576440759920E-06 -1.7992955061621650E-06 -1.9113052780103763E-06 -2.0286901389512177E-06 -2.1516606415331051E-06 -2.2804350187034426E-06 -2.4152394310872636E-06 -2.5563083079027624E-06 -2.7038844843216045E-06 -2.8582197438777868E-06 -3.0195749023229479E-06 -3.1882202724624733E-06 -3.3644359027379918E-06 -3.5485119460977649E-06 -3.7407491642350640E-06 -3.9414589262551269E-06 -4.1509641382851179E-06 -4.3695990110337445E-06 -4.5977100507762175E-06 -4.8356560427699264E-06 -5.0838087639862793E-06 -5.3425532569055597E-06 -5.6122884074552324E-06 -5.8934274472166129E-06 -6.1863983324285445E-06 -6.4916443544476082E-06 -6.8096246729736615E-06 -7.1408148233050348E-06 -7.4857073663466160E-06 -7.8448123534719423E-06 -8.2186581677451647E-06 -8.6077918499895610E-06 -9.0127800448027894E-06 -9.4342095113195513E-06 -9.8726878713010602E-06 -1.0328844396557176E-05 -1.0803330663218035E-05 -1.1296821332006992E-05 -1.1810015156914391E-05 -1.2343635521207046E-05 -1.2898431472178208E-05 -1.3475178666682876E-05 -1.4074680132891332E-05 -1.4697767371758059E-05 -1.5345301279373265E-05 -1.6018173117732316E-05 -1.6717305719808355E-05 -1.7443654480385057E-05 -1.8198208529859160E-05 -1.8981991843544504E-05 -1.9796064554734207E-05 -2.0641524086673505E-05 -2.1519506743021112E-05 -2.2431188517226751E-05 -2.3377787082283887E-05 -2.4360562797541532E-05 -2.5380820389233778E-05 -2.6439910464451992E-05 -2.7539231118879780E-05 -2.8680229531221442E-05 -2.9864403726921839E-05 -3.1093304276952371E-05 -3.2368536208118908E-05 -3.3691760835780107E-05 -3.5064697726482231E-05 -3.6489126756711134E-05 -3.7966890096985086E-05 -3.9499894519892859E-05 -4.1090113601951998E-05 -4.2739589949557737E-05 -4.4450437660939279E-05 -4.6224844887594094E-05 -4.8065076182381436E-05 -4.9973475389356750E-05 -5.1952468304010235E-05 -5.4004565395141194E-05 -5.6132364917860385E-05 -5.8338555913857092E-05 -6.0625921285864183E-05 -6.2997341077267185E-05 -6.5455795891380662E-05 -6.8004370316949382E-05 -7.0646256581551295E-05 -7.3384758288961381E-05 -7.6223294178539064E-05 -7.9165402192720133E-05 -8.2214743614447426E-05 -8.5375107375823092E-05 -8.8650414300280863E-05 -9.2044721932839547E-05 -9.5562229046843941E-05 -9.9207280726495422E-05 -1.0298437322251823E-04 -1.0689815942198196E-04 -1.1095345410468118E-04 -1.1515523958012534E-04 -1.1950867157537293E-04 -1.2401908518649147E-04 -1.2869200099315846E-04 -1.3353313171734677E-04 -1.3854838866117513E-04 -1.4374388868078475E-04 -1.4912596131832879E-04 -1.5470115609067598E-04 -1.6047625024161115E-04 -1.6645825654661685E-04 -1.7265443145040454E-04 -1.7907228358857117E-04 -1.8571958248698818E-04 -1.9260436756193187E-04 -1.9973495754019229E-04 -2.0711996019481016E-04 -2.1476828214823465E-04 -2.2268913956843245E-04 -2.3089206850473518E-04 -2.3938693635619472E-04 -2.4818395313822359E-04 -2.5729368342664873E-04 -2.6672705869486458E-04 -2.7649538998180068E-04 -2.8661038111305574E-04 -2.9708414231880955E-04 -3.0792920443418705E-04 -3.1915853326559032E-04 -3.3078554499628231E-04 -3.4282412162661512E-04 -3.5528862725275076E-04 -3.6819392475201124E-04 -3.8155539328966651E-04 -3.9538894606046265E-04 -4.0971104895842818E-04 -4.2453873988037313E-04 -4.3988964851971303E-04 -4.5578201702233304E-04 -4.7223472139438664E-04 -4.8926729332411786E-04 -5.0689994340622445E-04 -5.2515358459660733E-04 -5.4404985662930992E-04 -5.6361115157002020E-04 -5.8386063995839309E-04 -6.0482229803772458E-04 -6.2652093590358075E-04 -6.4898222662280254E-04 -6.7223273639135364E-04 -6.9629995587073006E-04 -7.2121233246363198E-04 -7.4699930386504872E-04 -7.7369133270490179E-04 -8.0131994259618881E-04 -8.2991775523052851E-04 -8.5951852908836110E-04 -8.9015719910798773E-04 -9.2186991828330797E-04 -9.5469410041349237E-04 -9.8866846448825802E-04 -1.0238330806779865E-03 -1.0602294178429115E-03 -1.0979003930820129E-03 -1.1368904227067453E-03 -1.1772454752311740E-03 -1.2190131263392671E-03 -1.2622426156950605E-03 -1.3069849059502993E-03 -1.3532927437725057E-03 -1.4012207232277417E-03 -1.4508253514236729E-03 -1.5021651165124264E-03 -1.5553005582497107E-03 -1.6102943411055925E-03 -1.6672113301154431E-03 -1.7261186695038072E-03 -1.7870858641370366E-03 -1.8501848641448214E-03 -1.9154901526138516E-03 -1.9830788364628709E-03 -2.0530307409285624E-03 -2.1254285072382587E-03 -2.2003576943233970E-03 -2.2779068841509739E-03 -2.3581677909664655E-03 -2.4412353749428553E-03 -2.5272079597283771E-03 -2.6161873549276353E-03 -2.7082789827384659E-03 -2.8035920100031486E-03 -2.9022394847603486E-03 -3.0043384785074859E-03 -3.1100102336123745E-03 -3.2193803166621878E-03 -3.3325787776678712E-03 -3.4497403154375751E-03 -3.5710044495729253E-03 -3.6965156988916122E-03 -3.8264237673693116E-03 -3.9608837368779078E-03 -4.1000562679838863E-03 -4.2441078085045858E-03 -4.3932108106070154E-03 -4.5475439562377923E-03 -4.7072923922746408E-03 -4.8726479742584186E-03 -5.0438095209892255E-03 -5.2209830788255765E-03 -5.4043821971299444E-03 -5.5942282147903484E-03 -5.7907505587974917E-03 -5.9941870550996434E-03 -6.2047842523941712E-03 -6.4227977592930868E-03 -6.6484925960343310E-03 -6.8821435606586543E-03 -7.1240356107552380E-03 -7.3744642618562171E-03 -7.6337360021330640E-03 -7.9021687256095648E-03 -8.1800921836265635E-03 -8.4678484560890728E-03 -8.7657924431433464E-03 -9.0742923784924833E-03 -9.3937303650199790E-03 -9.7245029344606299E-03 -1.0067021631519289E-02 -1.0421713624421007E-02 -1.0789022342475576E-02 -1.1169408142554986E-02 -1.1563349005726536E-02 -1.1971341265462744E-02 -1.2393900369130576E-02 -1.2831561674471420E-02 -1.3284881282778382E-02 -1.3754436910643918E-02 -1.4240828802219399E-02 -1.4744680684298288E-02 -1.5266640765987183E-02 -1.5807382785759889E-02 -1.6367607107942814E-02 -1.6948041871499283E-02 -1.7549444193576846E-02 -1.8172601430890153E-02 -1.8818332501925886E-02 -1.9487489272946044E-02 -2.0180958011458028E-02 -2.0899660910588414E-02 -2.1644557687866137E-02 -2.2416647262620191E-02 -2.3216969516386680E-02 -2.4046607139781337E-02 -2.4906687571473986E-02 -2.5798385033695928E-02 -2.6722922669104116E-02 -2.7681574784990236E-02 -2.8675669209946110E-02 -2.9706589769273858E-02 -3.0775778885395847E-02 -3.1884740309619922E-02 -3.3035041992441345E-02 -3.4228319099795970E-02 -3.5466277182339766E-02 -3.6750695506389167E-02 -3.8083430554758026E-02 -3.9466419706161160E-02 -4.0901685102661227E-02 -4.2391337714850395E-02 -4.3937581614703070E-02 -4.5542718467042373E-02 -4.7209152250456285E-02 -4.8939394219301248E-02 -5.0736068119182222E-02 -5.2601915667767882E-02 -5.4539802315075901E-02 -5.6552723295787657E-02 -5.8643809988549227E-02 -6.0816336596541745E-02 -6.3073727164411314E-02 -6.5419562947596238E-02 -6.7857590149699040E-02 -7.0391728045259894E-02 -7.3026077504042733E-02 -7.5764929935422720E-02 -7.8612776669788970E-02 -8.1574318795726589E-02 -8.4654477471361442E-02 -8.7858404728316256E-02 -9.1191494787032007E-02 -9.4659395902747440E-02 -9.8268022760007387E-02 -1.0202356943484235E-01 -1.0593252294214249E-01 -1.1000167738614544E-01 -1.1423814873038771E-01 -1.1864939020320382E-01 -1.2324320835289093E-01 -1.2802777976594218E-01 -1.3301166845874757E-01 -1.3820384395253266E-01 -1.4361370003692955E-01 -1.4925107422554015E-01 -1.5512626790330003E-01 -1.6125006716018109E-01 -1.6763376430244850E-01 -1.7428918002577087E-01 -1.8122868622880345E-01 -1.8846522943908206E-01 -1.9601235481363780E-01 -2.0388423066906236E-01 -2.1209567348408154E-01 -2.2066217330704560E-01 -2.2959991948711558E-01 -2.3892582663385070E-01 -2.4865756069328834E-01 -2.5881356501101427E-01 -2.6941308623293508E-01 -2.8047619987177225E-01 -2.9202383534403970E-01 -3.0407780025461661E-01 -3.1666080367732585E-01 -3.2979647814756652E-01 -3.4350940004754205E-01 -3.5782510802692907E-01 -3.7277011905940777E-01 -3.8837194169043698E-01 -4.0465908598224420E-01 -4.2166106960895766E-01 -4.3940841949750709E-01 -4.5793266834798119E-01 -4.7726634530150003E-01 -4.9744295995225357E-01 -5.1849697882588908E-01 -5.4046379336579276E-01 -5.6337967838424141E-01 -5.8728173984710774E-01 -6.1220785076562823E-01 -6.3819657387317097E-01 -6.6528706966178797E-01 -6.9351898825009795E-01 -7.2293234344668300E-01 -7.5356736726450313E-01 -7.8546434303209745E-01 -8.1866341514024366E-01 -8.5320437335398991E-01 -8.8912640952029998E-01 -9.2646784440309571E-01 -9.6526582229151559E-01 -1.0055559709508963E+00 -1.0473720244253966E+00 -1.0907454061595643E+00 -1.1357047698878313E+00 -1.1822754957507353E+00 -1.2304791391411511E+00 -1.2803328298677223E+00 -1.3318486193544301E+00 -1.3850327737820773E+00 -1.4398850113267412E+00 -1.4963976819736926E+00 -1.5545548887897116E+00 -1.6143315500351281E+00 -1.6756924021005941E+00 -1.7385909439711649E+00 -1.8029683247705843E+00 -1.8687521769263791E+00 -1.9358553986416531E+00 -2.0041748906702979E+00 -2.0735902538828213E+00 -2.1439624557913826E+00 -2.2151324760850777E+00 -2.2869199433176299E+00 -2.3591217771962048E+00 -2.4315108534436147E+00 -2.5038347109458381E+00 -2.5758143238441775E+00 -2.6471429643766240E+00 -2.7174851855914026E+00 -2.7864759565220507E+00 -2.8537199859856992E+00 -2.9187912747953488E+00 -2.9812329397981050E+00 -3.0405573566853987E+00 -3.0962466718766990E+00 -3.1477537368381223E+00 -3.1945035208381465E+00 -3.2358950602079521E+00 -3.2713040035017484E+00 -3.3000858123479091E+00 -3.3215796770462691E+00 -3.3351132038666229E+00 -3.3400079273134962E+00 -3.3355856950862153E+00 -3.3211759658346955E+00 -3.2961240498399680E+00 -3.2598003102013102E+00 -3.2116103267641942E+00 -3.1510060067046179E+00 -3.0774976042545350E+00 -2.9906665874368703E+00 -2.8901792618929547E+00 -2.7758010310235024E+00 -2.6474111379461975E+00 -2.5050176985435484E+00 -2.3487727966106884E+00 -2.1789873724523536E+00 -1.9961455960034034E+00 -1.8009183755911349E+00 -1.5941756148923498E+00 -1.3769967946371158E+00 -1.1506794234348805E+00 -9.1674487501357971E-01 -6.7694110840760235E-01 -4.3324175430885659E-01 -1.8784104581286171E-01 5.6855924265061017E-02 2.9824812425346903E-01 5.3355916549779214E-01 7.5986399809867944E-01 9.7412213667016045E-01 1.1732177906004635E+00 1.3540072286659879E+00 1.5133736621778087E+00 1.6482898854238941E+00 1.7558888668966628E+00 1.8335424370620039E+00 1.8789481616912223E+00 1.8902244117044753E+00 1.8660135206233892E+00 1.8055927277623212E+00 1.7089922937357955E+00 1.5771196815182422E+00 1.4118879364076415E+00 1.2163452618169492E+00 9.9480113641467716E-01 7.5294198291469072E-01 4.9792618045072545E-01 2.3844388403008077E-01 -1.5278571837740984E-02 -2.5155721014734039E-01 -4.5744858234893720E-01 -6.1911552581018714E-01 -7.2242198415947234E-01 -7.5383425406121785E-01 -7.0172427029000628E-01 -5.5819101187573694E-01 -3.2153845900610517E-01 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 </projector_function> <kinetic_energy_differences> 1.1359909660566248E+00 -1.0862860365914866E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 -1.0862860365914866E+00 1.9861177071042196E+01 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 3.4810448101763153E-01 6.7162816174423878E-01 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 6.7162816174423878E-01 1.3509953865906322E+01 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 8.5407571684507015E+00 -8.6500906295345033E+01 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 -8.6500906295345033E+01 8.7438771835042724E+02 </kinetic_energy_differences> <exact_exchange_X_matrix> -5.2263170706681281E-02 -4.1699730593300101E-02 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 -4.1699730593300101E-02 -8.7078369737052963E-01 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 -1.7339769912549895E-02 -8.9650147405751057E-02 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 -8.9650147405751057E-02 -1.3802642482991614E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 -5.5457277328699850E-01 5.0892864185938604E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 0.0000000000000000E+00 5.0892864185938604E+00 -4.7388881770313198E+01 </exact_exchange_X_matrix> <exact_exchange core-core=" -5.2700240846708965E+01"/> <!-- Program: atompaw - input data follows: Ni 28 ! Definition of material GGA-PBE scalarrelativistic loggrid 700 ! All-electrons calc.: GGA+scalar-relativstic - log.grid with 700 pts 4 4 3 0 0 0 ! Max. n per angular momentum: 4s 3p 3d 3 2 8 ! Partially occupied states: 3d: occ=8 4 1 0 ! 4p: occ=0 0 0 0 ! End of occupation section c ! 1s: core state c ! 2s: core state c ! 3s: core state v ! 4s: valence state c ! 2p: core state c ! 3p: core state v ! 4p: valence state v ! 3d: valence state 2 ! Max. l for partial waves basis 2.3 ! r_PAW radius y ! Do we add an additional s partial wave ? yes 3. ! Reference energy for this new s partial wave (Ryd) n ! Do we add an additional s partial wave ? no y ! Do we add an additional p partial wave ? yes 4. ! Reference energy for this p new partial wave (Ryd) n ! Do we add an additional p partial wave ? no y ! Do we add an additional d partial wave ? yes 1. ! Reference energy for this new d partial wave (Ryd) n ! Do we add an additional s partial wave ? no custom rrkj ! Scheme for PS partial waves and projectors 3 0. troulliermartins ! Scheme for pseudopotential (l_loc=3, E_loc=0Ry) 2.2 ! r_c matching radius for first s partial wave 2.2 ! r_c matching radius for second s partial wave 2.3 ! r_c matching radius for first p partial wave 2.3 ! r_c matching radius for second p partial wave 2.3 ! r_c matching radius for first d partial wave 2.3 ! r_c matching radius for second d partial wave XMLOUT default ! All parameters set to default for ABINIT file END Program: atompaw - input end --> </paw_dataset>
ABINIT computes the converged ground state of ferromagnetic FCC Nickel for several volumes around equilibrium.
Plot the etotal vs acell curve:
From this graph and output file, you can extract some physical quantities:
Equilibrium cell parameter: a0 = 3.523 angstrom
Bulk modulus: B = 199 GPa
Magnetic moment at equilibrium: mu = 0.60
Compare these results with published results:
- all-electron GGA-FLAPW from [Kresse1999]:
a0 = 3.52 angstrom
B = 200 GPa
mu = 0.60
- GGA-PAW with VASP code from [Kresse1999]:
a0 = 3.52 angstrom
B = 194 GPa
mu = 0.61
- Experimental results from from [Dewaele2008]:
a0 = 3.52 angstrom
B = 183 GPa
You should always compare results with all-electron ones (or other PAW computations). Not with experimental ones!
Additional remark:
It can be useful to test the sensitivity of results to some ATOMPAW input parameters
(see user’s guide for details on keywords):
- The analytical form and the cut-off radius \(r_{shape}\) of the shape function used in
compensation charge density definition,
By default a
sincfunction is used but agaussianshape can have an influence on results.Besselshapes are efficient and generally need a smaller cut-off radius (\(r_{shape}=0.8~r_{PAW}\)). - The matching radius \(r_{core}\) used to generate the pseudo core density from atomic core density,
- The inclusion of additional (“semi-core”) states in the set of valence electrons,
- The pseudization scheme used to get pseudopotential \(Vloc(r)\).
All these parameters have to be meticulously checked, especially if the PAW dataset is used for non-standard solid structures or thermodynamical domains.
Optional_exercise
Let’s add 3s and 3p semi-core states in PAW dataset!
Repeat the procedure (ATOMPAW + ABINIT) with
$ABI_HOME/doc/tutorial/paw2_assets/Ni.atompaw.input.semicore
file. The execution time is a bit longer as more electrons have to be treated by ABINIT.
Look at \(a_0\), \(B\) or \(\mu\) variation.
Note: this new PAW dataset has a smaller \(r_{PAW}\) radius (because semi-core states are localized).
a0 = 3.518 angstrom
B = 194 GPa
mu = 0.60
9 The Real Space Optimization (RSO) - for experienced users¶
In this section, an additional optimization of the atomic data is presented.
It can contribute, in some cases, to a speedup of the convergence on ecut.
This optimization is not essential to produce efficient PAW datasets but can be useful.
We advise experienced users to try it.
The idea is quite simple: when expressing the different atomic radial functions (\(\phi_i, \tphi_i, \tprj_i\)) on the plane wave basis, the number of plane waves depends on the “locality” of these radial functions in reciprocal space.
In this paper a method to enforce the locality (in reciprocal space) of projectors \(\tprj_i\) is presented; the projectors expressed in reciprocal space \(\tprj_i(g)\) are modified according to the following scheme: The reciprocal space is divided in 3 regions:
-
If \(g \lt g_{max}\), \(\tprj_i(g)\) is unchanged
-
If \(g \gt \gamma\), \(\tprj_i(g)\) is set to zero
-
If \(g_{max} \le g \le \gamma\), \(\tprj_i(g)\) is modified so that the contribution of \(\tprj_i(r)\) is conserved with an error \(W\) (as small as possible).
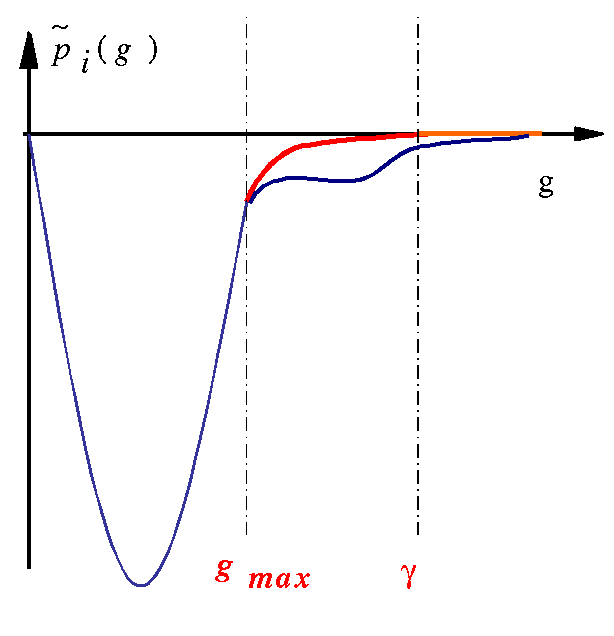
The above transformation of \(\tprj_i(g)\) is only possible if \(\tprj_i(r)\) is defined outside the spherical augmentation region up to a radius \(R_0\), with \(R_0 > r_c\). In practice we have to:
- Impose an error \(W\) (\(W\) is the maximum error admitted on total energy)
- Adjust \(g_{max}\) according to \(E_{cut}\) (\(g_{max} \le E_{cut}\))
- Choose \(\gamma\) so that \(2 g_{max} \lt \gamma \lt 3 g_{max}\)
and let the ATOMPAW code apply the transformation to \(\tprj_i\) and deduce \(R_0\) radius.
You can test it now. In your working directory, use the dataset $ABI_HOME/doc/tutorial/paw2_assets/Ni.atompaw.input3 (Bloechl’s projectors).
Ni 28 ! Definition of material GGA-PBE scalarrelativistic loggrid 700 ! All-electrons calc.: GGA+scalar-relativstic - log.grid with 2000 pts 4 4 3 0 0 0 ! Max. n per angular momentum: 4s 3p 3d 3 2 8 ! Partially occupied states: 3d: occ=8 4 1 0 ! 4p: occ=0 0 0 0 ! End of occupation section c ! 1s: core state c ! 2s: core state c ! 3s: core state v ! 4s: valence state c ! 2p: core state c ! 3p: core state v ! 4p: valence state v ! 3d: valence state 2 ! Max. l for partial waves basis 2.3 ! r_PAW radius y ! Do we add an additional s partial wave ? yes 3. ! Reference energy for this new s partial wave (Ryd) n ! Do we add an additional s partial wave ? no y ! Do we add an additional p partial wave ? yes 4. ! Reference energy for this p new partial wave (Ryd) n ! Do we add an additional p partial wave ? no y ! Do we add an additional d partial wave ? yes 1. ! Reference energy for this new d partial wave (Ryd) n ! Do we add an additional s partial wave ? no bloechl ! Scheme for PS partial waves and projectors 3 0. troulliermartins ! Scheme for pseudopotential (l_loc=3, E_loc=0Ry) XMLOUT ! Option for XML dataset creation default ! All parameters set to default for XML dataset END ! End of file
Replace the XML options (penultimate line):
XMLOUT
default
XMLOUT
rsoptim 8. 2 0.0001
Run ATOMPAW.
You get a new PAW dataset file for ABINIT.
Run ABINIT with it using the tpaw2_1.abi file.
Compare the results with those obtained in section 7.
You can try several values for \(g_{max}\) (keeping \(\frac{\gamma}{g_{max}}\) and \(W\) constant) and compare the efficiency of the atomic data; do not forget to test physical properties again.
Note
How to choose the RSO parameters? \(\frac{\gamma}{g_{max}} = 2\) and \(0.0001 \lt W \lt 0.001\) is a good choice. \(g_{max}\) has to be adjusted. The lower \(g_{max}\) the faster the convergence is but too low \(g_{max}\) can produce unphysical results.